Машина опорных векторов
Материал из MachineLearning.
Машина опорных векторов — является одной из наиболее популярных методологий обучения по прецедентам, предложенной В. Н. Вапником и известной в англоязычной литературе под названием SVM (Support Vector Machine).
Оптимальная разделяющая гиперплоскость. Понятие зазора между классами (margin). Случай линейной разделимости. Задача квадратичного программирования. Опорные векторы. Случай отсутствия линейной разделимости. Функции ядра (kernel functions), спрямляющее пространство, теорема Мерсера. Способы построения ядер. Примеры ядер. Сопоставление SVM и нейронной RBF-сети. Обучение SVM методом активных ограничений. SVM-регрессия.
Содержание
Машина опорных векторов в задачах классификации
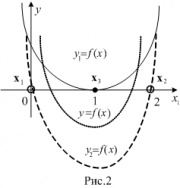
Понятие оптимальной разделяющей гиперплоскости
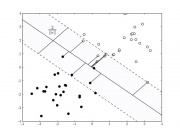
Линейно разделимая выборка
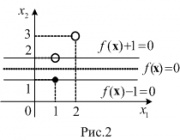
Без ограничения общности можно считать, что метки классов равны
Умножая, если нужно, функцию на некоторое положительное число, нетрудно видеть, что система неравенств (1) равносильна системе
Кроме того, так как — линейная функция, то последняя система неравенств примет вид
Для надежного разделения классов необходимо, чтобы расстояние между разделяющими гиперплоскостями было как можно большим, т.е. была как можно меньше. Таким образом, ставится задача нахождения минимума квадратичного функционала (коэффициент 0.5 вводится для удобства дифференцирования) в выпуклом многограннике, задаваемым системой неравенств (2). В выпуклом множестве квадратичный функционал всегда имеет единственный минимум (если это множество не пусто). Из теоремы Куна — Таккера следует, что решение этой оптимизационной задачи равносильно поиску седловой точки лагранжиана
Последнее условие равносильно тому, что
Из необходимых условий существования седловой точки (полагая ) имеем
Откуда следует, что вектор следует искать в виде
Найдем значения множителей Лагранжа, как критических точек лагранжиана. Для этого подставим (4) и (5) в лагранжиан, получим
Таким образом, задача сводится к нахождению критических точек функции
Линейно неразделимая выборка
Теорема 1. Функция является ядром тогда и только тогда, когда она удовлетворяет условиям:
Упражнение. Докажите, что следующие функции являются ядрами:
Теорема 2. Справедливы следующие свойства ядер:
Таким образом, это ядро гарантирует разделение любых векторов на любые два класса. В этом случае нахождение разделяющих функций осуществляется следующим образом:
1) найдем наибольшее значение функции
2) разделяющую функцию ищем в виде
Преимущества и недостатки SVM:
Составим нормальную систему
Ядра и спрямляющие пространства
Наиболее распространенные ядра:
Алгоритмы настройки
Машина опорных векторов в задачах регрессии
Постановка задачи
Анализ задачи
В таком случае функционал потерь принимает вид
.
Теперь мы можем записать задачу минимизации в виде задачи квадратичного программирования.
Опорные векторы и двойственная задача
Таким образом, все объекты делятся на 5 типов:
Мультиклассовый метод опорных векторов
В случае нескольких классов на практике зачастую применяется решающее правило, основанное на разбиении задачи на бинарные по схеме «один против остальных» (One-vs-Rest):
Стоит отметить, что дальнейшее обобщение такого решающего правила приводит к методу опорных векторов со структурированным результатом (Structured Output SVM).
Для обучения параметров такой композиции алгоритмов может быть решено стандартных для метода опорных векторов задач оптимизации, однако данный подход имеет свои недостатки. В работе Краммера и Зингера была предложена следующая совместная формулировка задачи оптимизации
Двойственная задача такой формулировки имеет вид
Программные реализации
Наиболее развитая и популярная реализация SVM на С++. Библиотека адаптирована для больших выборок и имеет эффективную реализацию скользящего контроля. Включены стандартные ядерные функции и допускается использование предварительно вычисленных матриц ядерных функций.
Эффективные и простые в использовании реализации SVM на С++ со схожими интерфейсами. В LibLinear реализована только линейная классификация и регрессия. Работают с большими выборками.
Полное руководство по опорных векторов (SVM)
Дата публикации Jul 29, 2019
Понять его внутреннюю работу и реализовать SVM в четырех различных сценариях
Введение
Мы видели, как подойти к проблеме классификации слогистическая регрессия, LDA, а такжедеревья решений, Теперь еще один инструмент представлен для классификации:Машина опорных векторов,
Машина опорных векторов является обобщением классификатора, называемогоклассификатор максимальной маржи, Классификатор максимального запаса прост, но его нельзя применять к большинству наборов данных, поскольку классы должны быть разделены линейной границей.
Вот почемуклассификатор опорных векторовбыл введен в качестве расширения классификатора максимальной маржи, который может применяться в более широком диапазоне случаев.
В заключение,Машина опорных векторовэто просто дальнейшее расширение классификатора опорных векторов для учета нелинейных границ классов.
Может использоваться как для двоичной, так и для мультиклассовой классификации.
Объяснение теории SVM может быть очень техническим. Надеюсь, эта статья поможет вам понять, как работают SVM.
Как только теория будет рассмотрена, вы сможете реализовать алгоритм в четырех различных сценариях!
Без дальнейших действий, давайте доберемся до этого.
Классификатор максимальной маржи
Этот метод основан на разделении классов с использованием гиперплоскости.
Что такое гиперплоскость?
Математически гиперплоскость это просто:
ЕслиИксудовлетворяет приведенному выше уравнению, то точка лежит на плоскости. В противном случае он должен находиться на одной стороне плоскости, как показано ниже.
В общем, если данные могут быть идеально разделены с помощью гиперплоскости, то существует бесконечное число гиперплоскостей, поскольку они могут быть сдвинуты вверх или вниз или слегка повернуты, не вступая в контакт с наблюдением.
Вот почему мы используеммаксимальный запас гиперплоскостиилиоптимальная разделяющая гиперплоскостькоторая является разделяющей гиперплоскостью, наиболее удаленной от наблюдений. Мы рассчитываем перпендикулярное расстояние от каждого тренировочного наблюдения с учетом гиперплоскости. Это известно какприбыль, Следовательно, оптимальной разделяющей гиперплоскостью является та, которая имеет наибольшее поле.
Как вы можете видеть выше, есть три точки, которые равноудалены от гиперплоскости. Эти наблюдения известны какопорные векторыпотому что, если их положение смещается, гиперплоскость также смещается. Интересно, что это означает, что гиперплоскость зависит только от опорных векторов, а не от каких-либо других наблюдений.
Что если разделительной плоскости не существует?
В этом случае не существует классификатора максимальной маржи. Мы используем вспомогательный векторный классификатор, который можетпочтиразделить классы с помощьюмягкий крайназываетсяклассификатор опорных векторов.Однако дальнейшее обсуждение этого метода становится очень техническим, и поскольку это не самый идеальный подход, мы пока пропустим эту тему.
Машина опорных векторов (SVM)
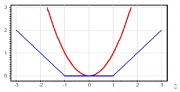
Не вдаваясь в технические детали, ядро - это функция, которая количественно определяет сходство двух наблюдений. Ядро может быть любой степени. Использование ядра со степенью больше единицы приводит к более гибкой границе принятия решений, как показано ниже.
Чтобы лучше понять, как выбор ядра может повлиять на алгоритм SVM, давайте реализуем его в четырех различных сценариях.
проект
Этот проект разделен на четыре мини-проекта.
Первая часть покажет, как выполнить классификацию с линейным ядром и как параметр регуляризацииСвлияет на результатгиперплоскость,
Затем вторая часть покажет, как работать сГауссово ядрогенерировать нелинейную гиперплоскость.
Третья часть имитирует перекрывающиеся классы, и мы будем использоватьперекрестная проверкачтобы найти лучшие параметры для SVM.
Наконец, мы выполняем очень простуюклассификатор спамаиспользуя SVM.
Упомянутые выше упражнения были взяты из курса Эндрю Нг, доступного бесплатно на Coursera. Я просто решаю их с помощью Python, который не рекомендуется инструктором. Тем не менее, я очень рекомендую курс для любых начинающих
Как всегда, ноутбук и данные доступныВот,
Прежде чем начать, давайте импортируем несколько полезных библиотек:
Обратите внимание, что мы импортируемloadmatздесь, потому что наши данные в матричной форме.
Затем мы сохраняем пути к нашим наборам данных в разных переменных:
Наконец, мы создадим функцию, которая поможет нам быстро построить каждый набор данных:
Теперь в этой части мы реализуем машину опорных векторов, используя линейное ядро, и увидим, как параметр регуляризации может влиять на гиперплоскость.
Во-первых, давайте загрузим и визуализируем данные:
И вы должны увидеть:
Обратите внимание на график над наличием выброса с левой стороны, Давайте посмотрим, как параметр регуляризации повлияет на гиперплоскость при наличии выброса.
Приведенный выше блок кода просто подгоняет SVM к данным, и мы используем прогнозы для построения гиперплоскости. Обратите внимание, что мы используем параметр регуляризации 1. Результат должен быть следующим:
Как видите, гиперплоскость проигнорировала выброс. Следовательно, низкий параметр регуляризации будетобобщать лучше, Ошибка теста обычно будет выше, чем ошибка перекрестной проверки.
Теперь давайте увеличим параметр регуляризации:
Теперь выбросы направильносторона гиперплоскости, но это также означает, что мы переоснащаемся. В конечном счете, эта граница не будет хорошо работать на ненаблюдаемых данных.
Теперь мы знаем, что для размещения нелинейных границ нам нужно изменить функцию ядра. В этом упражнении мы будем использоватьГауссово ядро,
Во-первых, давайте построим наши данные:
И вы должны увидеть:
Перед внедрением SVM вы должны знать, что ядро Гаусса выражается как:
Обратите внимание, что есть параметрсигмаэто определяет, насколько быстро метрика подобия стремится к нулю, когда они находятся дальше друг от друга.
Поэтому мы реализуем его с помощью следующего кода:
И вы должны получить следующую гиперплоскость:
Удивительно! Гиперплоскость не является идеальной границей, но она довольно хорошо справилась с классификацией большинства данных. Я предлагаю вам попробовать разные значениясигмачтобы увидеть, как это влияет на гиперплоскость.
Перекрестная проверкаНеобходимо выбрать лучшие параметры настройки для оптимальной производительности из нашей модели. Давайте посмотрим, как можно применить это к SVM.
Конечно, давайте посмотрим, как выглядят данные для этого упражнения:
Обратите внимание, что у нас есть перекрывающиеся классы. Конечно, наша гиперплоскость не будет идеальной, но мы будем использовать перекрестную проверку, чтобы убедиться, что это лучшее, что мы можем получить:
Из приведенной выше ячейки кода вы должны получить, что лучший параметр регуляризации равен 1, и чтосигмадолжно быть 0,1. Используя эти значения, мы можем сгенерировать гиперплоскость:
Наконец, мы обучаем классификатора спама с помощью SVM. В этом случае мы будем использовать линейное ядро. Кроме того, у нас есть отдельные наборы данных для обучения и тестирования, что сделает наш анализ немного легче.
И вы видите, что мы получаемподготовкаточность 99,825%, атестточность 98,9%!
Это оно! Вы изучили внутреннюю работу машин опорных векторов и реализовали алгоритм в четырех различных мини-проектах, чтобы понять, как выбор ядра влияет на алгоритм и как работать с перекрестной проверкой.
Я надеюсь, что вы нашли эту статью полезной и что вы вернетесь к ней, когда захотите внедрить SVM.
Краткий обзор алгоритма машинного обучения Метод Опорных Векторов (SVM)
Предисловие
В данной статье мы изучим несколько аспектов SVM:
Как известно, задачи машинного обучения разделены на две основные категории — классификация и регрессия. В зависимости от того, какая из этих задач перед нами стоит, и какой у нас имеется датасет для этой задачи, мы выбираем какой именно алгоритм использовать.
Метод Опорных Векторов или SVM (от англ. Support Vector Machines) — это линейный алгоритм используемый в задачах классификации и регрессии. Данный алгоритм имеет широкое применение на практике и может решать как линейные так и нелинейные задачи. Суть работы “Машин” Опорных Векторов проста: алгоритм создает линию или гиперплоскость, которая разделяет данные на классы.
Теория
Основной задачей алгоритма является найти наиболее правильную линию, или гиперплоскость разделяющую данные на два класса. SVM это алгоритм, который получает на входе данные, и возвращает такую разделяющую линию.
Рассмотрим следующий пример. Допустим у нас есть набор данных, и мы хотим классифицировать и разделить красные квадраты от синих кругов (допустим позитивное и отрицательное). Основной целью в данной задаче будет найти “идеальную” линию которая разделит эти два класса.
Найдите идеальную линию, или гиперплоскость, которая разделит набор данных на синий и красный классы.
На первый взгляд, не так уж и сложно, правда?
Но, как вы можете заметить, нет одной, уникальной, линии, которая бы решала такую задачу. Мы можем подобрать бесконечное множество таких линий, которые могут разделить эти два класса. Как же именно SVM находит “идеальную” линию, и что в его понимании “идеальная”?
Взгляните на пример ниже, и подумайте какая из двух линий (желтая или зеленая) лучше всего разделяет два класса, и подходит под описаниие “идеальной”?
Какая линия лучше разделяет набор данных по вашему мнению?
Если вы выбрали желтую прямую, я вас поздравляю: это та самая линия, которую бы выбрал алгоритм. В данном примере мы можем интуитивно понять что желтая линия разделяет и соответственно классифицирует два класса лучше зеленой.
В случае с зеленой линией — она расположена слишком близко к красному классу. Несмотря на то, что она верно классифицировала все объекты текущего набора данных, такая линия не будет генерализованной — не будет так же хорошо вести себя с незнакомым набором данных. Задача нахождения генерализованной разделяющей двух классов является одной из основных задач в машинном обучении.
Как SVM находит лучшую линию
Алгоритм SVM устроен таким образом, что он ищет точки на графике, которые расположены непосредственно к линии разделения ближе всего. Эти точки называются опорными векторами. Затем, алгоритм вычисляет расстояние между опорными векторами и разделяющей плоскостью. Это расстояние которое называется зазором. Основная цель алгоритма — максимизировать расстояние зазора. Лучшей гиперплоскостью считается такая гиперплоскость, для которой этот зазор является максимально большим.
Довольно просто, не так ли? Рассмотрим следующий пример, с более сложным датасетом, который нельзя разделить линейно.
Очевидно, что этот набор данных нельзя разделить линейно. Мы не можем начертить прямую линию, которая бы классифицировала эти данные. Но, этот датасет можно разделить линейно, добавив дополнительное измерение, которое мы назовем осью Z. Представим, что координаты на оси Z регулируются следующим ограничением:
Таким образом, ордината Z представлена из квадрата расстояния точки до начала оси.
Ниже приведена визуализация того же набора данных, на оси Z.
Теперь данные можно разделить линейно. Допустим пурпурная линия разделяющая данные z=k, где k константа. Если
, то следовательно и
— формула окружности. Таким образом, мы можем спроэцировать наш линейный разделитель, обратно к исходному количеству измерений выборки, используя эту трансформацию.
В результате, мы можем классифицировать нелинейный набор данных добавив к нему дополнительное измерение, а затем, привести обратно к исходному виду используя математическую трансформацию. Однако, не со всеми наборами данных можно с такой же легкостью провернуть такую трансформацию. К счастью, имплементация этого алгоритма в библиотеке sklearn решает эту задачу за нас.
Гиперплоскость
Теперь, когда мы ознакомились с логикой алгоритма, перейдем к формальному определению гиперплоскости
Гиперплоскость — это n-1 мерная подплоскость в n-мерном Евклидовом пространстве, которая разделяет пространство на две отдельные части.
Например, представим что наша линия представлена в виде одномерного Евклидова пространства (т.е. наш набор данных лежит на прямой). Выберите точку на этой линии. Эта точка разделит набор данных, в нашем случае линию, на две части. У линии есть одна мера, а у точки 0 мер. Следовательно, точка — это гиперплоскость линии.
Для двумерного датасета, с которым мы познакомились ранее, разделяющая прямая была той самой гиперплоскостью. Проще говоря, для n-мерного пространства существует n-1 мерная гиперплоскость, разделяющая это пространство на две части.
Точки представлены в виде массива X, а классы к которому они принадлежат в виде массива y.
Теперь мы обучим нашу модель этой выборкой. Для данного примера я задал линейный параметр “ядра” классификатора (kernel).
Предсказание класса нового объекта
Настройка параметров
Параметры — это аргументы которые вы передаете при создании классификатора. Ниже я привел несколько самых важных настраиваемых параметров SVM:
Данный параметр помогает отрегулировать ту тонкую грань между “гладкостью” и точностью классификации объектов обучающей выборки. Чем больше значение “С” тем больше объектов обучающей выборки будут правильно классифицированы.
В данном примере есть несколько порогов принятия решений, которые мы можем определить для этой конкретной выборки. Обратите внимание на прямую (представлена на графике в виде зеленой линии) порога решений. Она довольно таки проста, и по этой причине, несколько объектов были классифицированы неверно. Эти точки, которые были классифицированы неправильно называются выбросами в данных.
Мы также можем настроить параметры таким образом, что в конечном итоге получим более изогнутую линию (светло-голубой порог решений), которая будет классфицировать асболютно все данные обучающей выборки правильно. Конечно, в таком случае, шансы того, что наша модель сможет генерализовать и показать столь же хорошие результаты на новых данных, катастрофически мала. Следовательно, если вы пытаетесь достигнуть точности при обучении модели, вам стоит нацелиться на что-то более ровное, прямое. Чем выше число “С” тем более запутанная гиперплоскость будет в вашей модели, но и выше число верно-классифицированных объектов обучающей выборки. Поэтому, важно “подкручивать” параметры модели под конкретный набор данных, чтобы избежать переобучения но, в то же время достигнуть высокой точности.
В официальной документации библиотека SciKit Learn говорится, что гамма определяет насколько далеко каждый из элементов в наборе данных имеет влияние при определении “идеальной линии”. Чем ниже гамма, тем больше элементов, даже тех, которые достаточно далеки от разделяющей линии, принимают участие в процессе выбора этой самой линии. Если же, гамма высокая, тогда алгоритм будет “опираться” только на тех элементах, которые наиболее близки к самой линии.
Если задать уровень гаммы слишком высоким, тогда в процессе принятия решения о расположении линии будут учавствовать только самые близкие к линии элементы. Это поможет игнорировать выбросы в данных. Алгоритм SVM устроен таким образом, что точки расположенные наиболее близко относительно друг друга имеют больший вес при принятии решения. Однако при правильной настройке «C» и «gamma» можно добиться оптимального результата, который построит более линейную гиперплоскость игнорирующую выбросы, и следовательно, более генерализуемую.
Заключение
Я искренне надеюсь, что эта статья помогла вам разобраться в сути работы SVM или Метода Опорных Векторов. Я жду от вас любых комментариев и советов. В последующих публикациях я расскажу о математической составляющей SVM и о проблемах оптимизации.