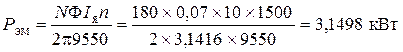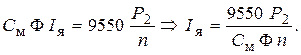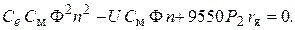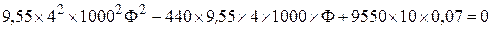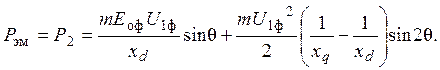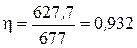Задачи по электрическим машинам и аппаратам

Примеры решения задач по электрическим аппаратам

1. Определить длительно допустимую величину плотности переменного тока для бескаркасной цилиндрической катушки индуктивности, намотанной медным проводом диаметром d = 4мм. Изоляция провода хлопчатобумажная без пропитки, число витков катушки w = 250, остальные необходимые размеры даны на рис. 1. Катушка находиться в спокойном воздухе.

Решение: Исходя из закона Джоуля-Ленса потери энергии, выделяющейся в катушке,

В длительном режиме работы вся выделенная энергия в катушке должна быть отведена в окружающую среду. Мощность, отводимая в окружающую среду, , где С – температура окружающей среды; в качестве ϑ берем величину допустимой температуры для данного класса изоляции ϑ_доп = 90 о С.

Поскольку должно быть равенство между выделенной в катушке и отводимой с ее поверхности тепловыми мощностями, то исходным уравнением для нахождения допустимой плотности тока будет:

– длина среднего витка катушки. Тогда

а плотность переменного тока

Решение: Уравнение кривой нагрева в простейшем случае имеет вид

где θ_уст = P/(k_xF) — установившееся превышение температуры. Расчет θ_уст и Т произведем на единице длины проводника l = 1 м, поэтому

Постоянная времени нагрева

где с — удельная теплоемкость меди; М = γ V— масса стержня длиной в 1 м; γ — плотность меди; V — объем проводника; F — охлаждающая поверхность.

3. Определить, какое количество тепла передается излучением в установившемся режиме теплообмена от нагретой шины к холодной, если шины размером 120 х 10 мм 2 расположены параллельно друг другу на расстоянии S = 20 мм. Шина, по которой протекает переменный ток, нагревается до температуры ϑ₁ = 120 °С. Температура другой шины ϑ₁ = 35 °С. Обе шины медные и окрашены масляной краской

Решение: Количество тепла, передающееся излучением от нагретой шины к холодной,

Рассчитаем теплообмен на длине шин l = 1м. Учитывая, что F₁φ₁₂= F₂φ₂₁, имеем

где F₁ – теплоотдающая поверхность нагретой шины.

Обозначения показаны на рис. 2: ; F_BC’C = F_BC = F_AD;

4. Определить установившееся значение температуры медного круглого стержня диаметром d = 10 мм на расстоянии 0,5 м от его торца, который находится в расплавленном олове, имеющем температуру ϑ_mах = 250°С. Стержень находится в воздухе с ϑ₀= 35°С, при этом коэффициент теплоотдачи с его поверхности k_т = 25 Вт/(м 2 ·град). Определить также тепловой поток, который отводится с боковой поверхности стержня длиной 0,5 м, считая от поверхности олова

Решение: Из формулы

где

Здесь λ = 390 Вт/(м·град) — коэффициент теплопроводности меди, температура стержня ϑ = 50,6°С.

Величина теплового потока с боковой поверхности стержня

Ответ: ϑ = 50,6°С; Р = 31,6 Вт.

5. Определить электродинамическое усилие, действующее на 10 м прямолинейного бесконечного тонкого уединенного проводника с током к.з. I = 50 кА. Проводник находится в поле земли и расположен под углом γ = 30° к плоскости магнитного меридиана. Горизонтальная составляющая напряженности магнитного поля Н = 12,7 А/м а угол наклонения β = 72°

Решение: Действующие на проводник усилия

где ; Г/м.

Тогда горизонтальная составляющая индукции земного поля:

Т;

Т.

Определим две составляющие силы, действующие на проводник:

от горизонтальной составляющей вектора индукции

Н.

Суммарное усилие, действующее на проводник,

Н.

6. Определить усилия, действующие на каждый из ножей терхполюсного разъединителя, по которому протекает предельный сквозной ток трехфазного К.З. Амплитудное значение тока I_max=320 кA, длина ножей l = 610 мм, расстояние меду ними h = 700 мм. Вычислить также требуемый момент сопротивления поперечного сечения ножей

Решение: В случае установившегося тока К.З. будут действовать знакопеременные времени усилия. Определим максимальные притягивающие и максимальные отталкивающие усилия на каждый из трех ножей разъединителя (рис. 3):

где

Наиболее напряженным будет средний полюс, поэтому его необходимо рассчитывать на прочность изгиба как балку на двух опорах. Требуемое значение момента сопротивления поперечного сечения

где – изгибающий момент;

Па – допустимое напряжение на изгиб для ножей, выполненных из меди

0твет:

7. Определить величину электродинамического усилия, действующего на 1 м круглого проводника диаметром d = 20 мм. Проводник расположен на расстоянии а/2 = 10 см вдоль ферромагнитной стенки и по нему протекает ток I = 1000 А

Решение: Поскольку диаметр проводника значительно меньше, чем расстояние до ферромагнитной стенки, то к решению следует подходить, как и в случае бесконечно тонкого проводника. Методом зеркального изображения найдем электродинамическое усилие, которое действует между данным проводником и его зеркальным изображением относительно поверхности ферромагнитной стенки с тем же током I.

где ;

8. Определить скорость движения открытой (свободной) дуги с током I_д = 400 А, находящейся в поперечном магнитном поле с индукцией B = 0,05 T

Решение: Для индукции в пределах 0

Источник

Примеры решения задач по машинам постоянного тока

Министерство сельского хозяйства и продовольствия

Республики Беларусь

Учреждение образования
«Белорусский государственный аграрный

Технический университет»

В помощь абитуриенту

ЭЛЕКТРИЧЕСКИЕ МАШИНЫ
И АППАРАТЫ

Специальность – Энергетическое обеспечение сельского хозяйства
(электроэнергетика)

Минск

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА

И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

АГРАРНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Перечень основных тем, образцы типовых задач

И экзаменационного задания

Для подготовки к вступительному экзамену

По дисциплине «Электрические машины и аппараты»

(для абитуриентов, окончивших аграрные колледжи)

Минск

Рекомендовано научно-методическим советом Учреждения образования «Белорусский государственный аграрный технический университет» (протокол №1 от 22.02.2007г.)

Составитель – Н.Е. Шевчик

В пособии изложены основные темы для подготовки к вступительному экзамену по дисциплине «Электрические машины и аппараты» для слушателей подготовительных курсов при агротехнических колледжах, даны типовые задачи и образец экзаменационного задания.

Предназначено для абитуриентов Учреждения образования «Белорусский государственный университет», окончивших аграрные колледжи.

УДК 321.313(07)

ББК 31.261я7

© БГАТУ, 2007
Содержание

Введение

Экзаменационное задание для вступительного испытания по дисциплине «Электрические машины и аппараты» состоит из задач различной степени сложности. С порядковым номером задачи сложность возрастает.

При проверке на ЭВМ проверяется цифра ответа. Если она не точна, задача считается не решенной, т.е. оценивается не только правильность решения, но и точность алгебраических преобразований и арифметических расчетов.

Экзаменационные задачи составлены по четырем разделам: машины постоянного тока, асинхронные машины, синхронные машины и трансформаторы.

Учебно-тематический план для слушателей подготовительных курсов составлен таким образом, чтобы максимально ориентировать учащихся на решение задач, и его назначение — дополнить основной курс «Электрические машины и аппараты».

В теоретической части приведена информация, на которую необходимо обратить внимание при подготовке к вступительным экзаменам. Она используется при решении задач в первую очередь. Но это не означает, что ее достаточно для подготовки к экзамену.

Примеры решения задач максимально приближены к тем, которые будут на вступительных экзаменах; в них указана размерность ответа.

В примере экзаменационного задания приведены задачи вступительного испытания по дисциплине «Электрические машины и аппараты» 2006 года.

ОСНОВНЫЕ ТЕМЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
по дисциплине «Электрические машины и аппараты»

№ Наименование темы

1. Вывод формулы электродвижущей силы (ЭДС) машины постоянного тока. Постоянная машины при расчете ЭДС. Уравнение равновесия напряжений МПТ

2. Вывод формулы момента МПТ. Постоянная машины при расчете момента, связь ее с постоянной машины при расчете ЭДС. Связь момента с мощностью и частотой вращения

3. Потери и КПД МПТ. Вывод формулы частоты вращения двигателей постоянного тока. Понятия «присоединенная, или подводимая мощность» и «полезная мощность» для генератора и двигателя

4. Расчет обмоточных данных и построение однослойной петлевой обмотки машины переменного тока, определение обмоточного коэффициента

5. Уравнение напряжений и векторная диаграмма синхронного генератора. Потери и КПД синхронной машины. Вывод формулы электромагнитной мощности синхронной машины

6. V-образные характеристики синхронных генератора и двигателя, синхронный компенсатор. Влияние работы синхронного двигателя с перевозбуждением на потери электроэнергии в линии электропередач

7. Принцип действия и устройство асинхронного двигателя (АД). Асинхронная машина с вращающимся ротором, рабочий режим

8. Схема замещения АД и ее анализ. Опыты холостого хода и короткого замыкания АД, определение по ним параметров схемы замещения

9. Потери и КПД АД. Вывод формулы электромагнитной мощности АД

10. Работа трансформатора при нагрузке, рабочий режим. Схема замещения и векторная диаграмма трансформатора. Опыты холостого хода и короткого замыкания, определение по ним параметров схемы замещения

11. Потери и КПД трансформатора. Зависимость вторичного напряжения трансформатора от степени и характера нагрузки

12. Параллельная работа трансформаторов при неодинаковых коэффициентах трансформации, напряжениях короткого замыкания, группах соединения обмоток

Машины постоянного тока

ЭДС машины постоянного тока:

, (1.1)

где Е — ЭДС машины постоянного тока, В;

Ф — основной магнитный поток, Вб;

— постоянная машины при расчете ЭДС.

, (1.2)

где — количество всех проводников в машине, шт.;

— количество пар полюсов, шт.;

— количество параллельных ветвей обмотки, шт.

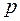
В простой петлевой обмотке .

Момент машины постоянного тока:

, (1.3)

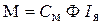
где М — момент машины постоянного тока, Н×м;

— ток якоря, А;

— постоянная машины при расчете момента,

. (1.4)

Соотношение между постоянными момента и ЭДС:

, (1.5)

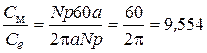
Уравнения равновесия напряжений:

, (1.6)

где — напряжение генератора, В;

— сопротивление якоря, Ом;

, (1.7)

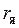
Частота вращения двигателя постоянного тока:

— с параллельным возбуждением:

; (1.8)

— с последовательным возбуждением:

, (1.9)

где к — коэффициент пропорциональности меду током и магнитным потоком в двигателе последовательного возбуждения.

Формула, связывающая момент, мощность на валу и частоту вращения якоря:

. (1.10)

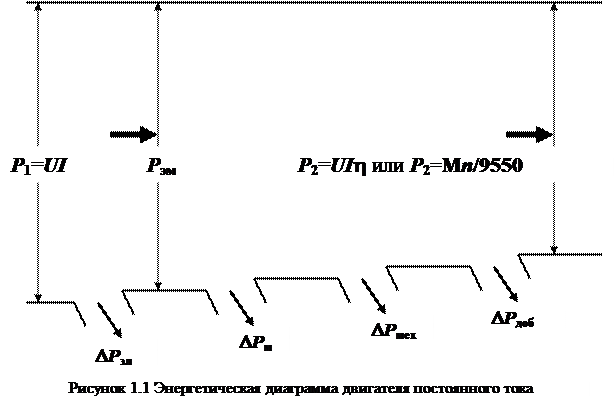
Потери, коэффициент полезного действия, подводимая или присоединенная мощность иллюстрируются энергетической диаграммой (рисунок 1.1)

Р₁ — подводимая или присоединенная мощность, Вт, двигатель потребляет ее из сети;

U — напряжение сети, В;

I — ток двигателя, А;

Р_эм — электромагнитная мощность двигателя, Вт; из рисунка видно:

где DР_эл — электрические потери двигателя, Вт;

, (1.12)

где — сопротивления соответственно обмоток параллельного возбуждения, якорной и последовательного возбуждения, Ом;

— падение напряжения на щётке, В;

— ток параллельной ветви, который идёт по щётке, А;

— количество щёток, шт.

(1.13)

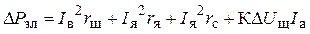
где DР_м — магнитные потери, Вт;

DР_мех — механические потери, Вт;

DР_доб — добавочные потери, Вт.

Коэффициент полезного действия двигателя

(1.14)

Двигатель потребляет электрическую мощность из сети, преобразует ее в механическую и через вал передает ее на рабочую машину. Часть мощности теряется в двигателе, что учитывается коэффициентом полезного действия.

У генератора наоборот: механическая мощность поступает через вал приводного двигателя (турбины), преобразуется в электрическую и поступает в электрическую сеть.

Примеры решения задач по машинам постоянного тока

Задача 1

Решение

Электромагнитная мощность двигателя (кВт):

.

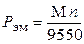
Электромагнитный момент машины постоянного тока (Н×м):

.

Постоянная машины при расчете момента

.

Ширина щетки равна ширине коллекторной пластины, обмотка простая петлевая, поэтому количество пар параллельных ветвей равно количеству пар полюсов: а = р, — тогда

.

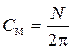
С учетом вышеизложенного

Задача 2

Решение

Частота вращения двигателя (падением напряжения на щетках пренебречь)

.

Сопротивление обмотки якоря определится из формулы равновесия ЭДС генератора:

.

Подставляем полученное выражение расчета сопротивления обмотки якоря в формулу частоты вращения двигателя:

.

Постоянная машины при определении ЭДС

Количество пар полюсов — р = 2 (из условия).

Ширина щетки равна ширине коллекторной пластины, обмотка простая петлевая, поэтому количество пар параллельных ветвей равно количеству пар полюсов: а = р, — тогда

.

Так как принято допущение, что индукция в воздушном зазоре постоянная по всей длине зазора, магнитный поток можно рассчитать по формуле:

Вб.

Частота вращения двигателя

Задача 3

Решение

Из уравнений: и определим ток якоря:

Полученное выражение подставим в формулу: . Получим

.

Сделав алгебраические преобразования, получим квадратное уравнение:

Для простой петлевой, одноходовой обмотки якоря а = р, поэтому

; .

Подставляем числовые значения в систему уравнений:

Корни уравнения: Ф₁ = 0; Ф₂ = 0,1096 Вб.

ОБЩИЕ ВОПРОСЫ МАШИН ПЕРЕМЕННОГО ТОКА.

СИНХРОННЫЕ МАШИНЫ

В основе действия любой машины переменного тока лежит вращающееся магнитное поле. Для получения указанного поля при трёхфазной системе должны выполняться два условия:

1. Обмотки фаз должны быть сдвинуты друг относительно друга на 120 электрических градусов (число электрических градусов в машине зависит от числа пар полюсов: на одну пару полюсов приходится 360 электрических градусов);

2. Токи в фазах должны быть сдвинуты во времени друг от друга на 1/3 периода.

Обмотка машины переменного тока строится по обмоточным данным:

(2.1)

где — расчетный шаг (равен полюсному делению, выраженному в зубцах);

— произвольное число меньше 1, доводящее расчетный шаг до целого числа.;

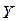
Р — число пар полюсов, шт.;

· число пазов на полюс и фазу определяет число секций в катушечной группе и находится по формуле:

(2.2)

где 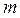— число фаз;

· число катушечных групп. Для однослойной обмотки

. (2.3)

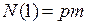
В двухслойной обмотке:

; (2.4)

· число электрических градусов на один паз:

; (2.5)

· параллельные ветви. Если катушечные группы одной фазы соединены последовательно, тогда число параллельных ветвей , если нет, тогда число параллельных ветвей увеличивается.

Число пар полюсов в машине переменного тока

, (2.6)

где f — частота тока, Гц;

Электродвижущая сила одной фазы обмотки машины переменного тока:

, (2.7)

где Ф — магнитный поток, Вб;

W — число витков обмотки, шт.;

К_об — обмоточный коэффициент;

, (2.8)

где К_у — коэффициент укорочения;

К_р — коэффициент распределения;

К_с — коэффициент скоса;

; , , (2.9)

где — угол укорочения, эл. град;

— угол скоса пазов.

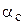
Электромагнитная мощность синхронной машины, подключенной к сети:

, (2.10)

где Е₀ — ЭДС, наводимая основным магнитным потоком, В; рассчитывается по формуле (2.7);

U_1ф — фазное напряжение сети, В;

x_d, x_q — индуктивное сопротивление реакции якоря по продольной и поперечной осям, Ом; для машины с неявнополюсным якорем x_d =x_q;

q — нагрузочный угол, град.

Уравнение равновесия напряжений синхронного генератора:

, (2.11)

где — вектор реакции якоря по продольной оси, В;

— вектор реакции якоря по поперечной оси, В;

— ЭДС, наводимая потоками рассеяния, В;

— вектор тока статора, А;

— активное сопротивление обмотки статора, Ом.

; ; (2.12)

где , — составляющие тока статора соответственно по продольной и поперечной осям, А;

— индуктивные сопротивления реакции якоря соответственно по продольной и поперечной осям, Ом;

(2.13)

где y₁ — угол между вектором тока I₁ и ЭДС E₀, град. (см. рисунок 2.1).

Упрощенная векторная диаграмма явнополюсного синхронного генератора, работающего на активно-индуктивную нагрузку, приведена на рисунке 2.1. При ее построении сделано допущение, что r₁ = 0, и потоки рассеяния также равны нулю. Тогда получается прямоугольный треугольник с катетами Е_1q и (E₀—Е₁_d) а также гипотенузой U₁. Облегчается решение задач.

Примеры решения задач по общим вопросам машин переменного тока
и синхронным машинам

Задача 1

Решение

где Y и Y_у — соответственно диаметральный и укороченный шаги обмотки;

.

Число пазов на полюс и фазу q = Z/2Pm.

Число электрических градусов, приходящихся на один паз, a = 360Р/Z.

Скоса пазов нет, поэтому К_с=1.

Р = 60 ´ 50/1500 = 2 ; Y = 36/(2 ´ 2) = 9; Y_у = Y – 1 = 9 – 1 = 8;

К_у = sin (8 ´ 90 о /9) = 0,9848; q = 36/(2 ´ 2 ´ 3)=3;

a = 360 ´ 2/36 = 20 эл. град ; ;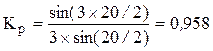

Задача 2

Решение

КПД генератора определится по формуле: ,

где Р₁ — мощность, передаваемая на вал генератора от приводного двигателя, ;

Р₂ — полезная мощность генератора, если пренебречь потерями в обмотке статора, она равна электромагнитной:

В условии указано: «Напряжение сети U₁ = 380 В». Это линейное напряжение, при соединении «звезда»

В.

кВт.

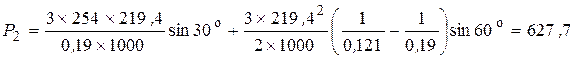
АСИНХРОННЫЕ МАШИНЫ

Мощность на валу трехфазного асинхронного двигателя 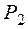(Вт) можно определить по формуле:

, (3.1)

где 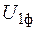— фазное напряжение, подаваемое на двигатель, В;

— фазный ток статора, А;

cosφ₁ — коэффициент мощности;

— коэффициент полезного действия.

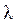
Частота вращения ротора

, (3.2)

, (3.3)

где — частота тока, Гц;

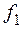
Р — число пар полюсов;

— скольжение; .

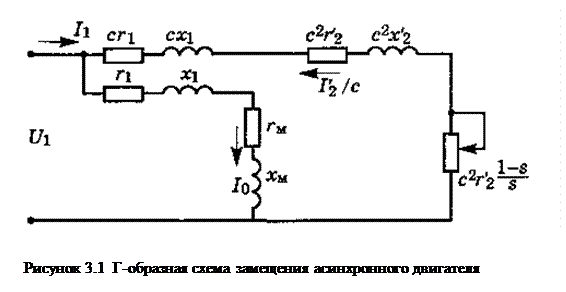
Схема замещения (Г-образная) асинхронного двигателя приведена на рисунке 3.1.

На рисунке 3.1 U_1ф — фазное напряжение, В; С — коэффициент, примем С = 1; r₁, x₁ — сопротивления обмотки статора, Ом; r’₂, x‘₂ — приведенные сопротивления обмотки ротора, Ом; r_м, x_м — сопротивления намагничивающей ветви, Ом; I₁ — ток статора, А; I₀ — намагничивающий ток, А; I’₂ — приведенный ток ротора, А.

Параметры схем определятся из опытов короткого замыкания и холостого хода по следующим формулам:

; ; , (3.4)

где r_к — активное сопротивление короткого замыкания, Ом;

Р_к — потери короткого замыкания, Вт

I_н — номинальный ток двигателя, А;

z_к — полное сопротивление короткого замыкания, Ом;

U_кф — фазное напряжение короткого замыкания, В.

Приведенные сопротивления обмотки ротора приблизительно равны сопротивлениям обмотки статора:

; . (3.5)

Параметры намагничивающей ветви:

; ; , (3.6)

где Р_х — потери холостого хода, Вт;

I_х — холостой ток двигателя, А;

Z_м — полное сопротивление намагничивающей ветви, Ом;

U_хф — фазное напряжение холостого хода, В.

Мощность на валу двигателя Р₂ будет соответствовать тепловым потерям на переменном сопротивлении r’₂(1–s)/s:

. (3.7)

Приведенный ток ротора I’₂ также определяется по схеме замещения (рисунок 3.1):

, (3.8)

где Р_х — потери холостого хода, Вт.

При подстановке выражения (3.8) в формулу (3.7) получим уравнение мощности на валу:

. (3.9)

Из формулы (3.9) видно, что мощность асинхронного двигателя пропорциональна квадрату питающего напряжения.

Для асинхронного двигателя также справедливы формулы (1.10) и (1.14).

При решении задач нужно помнить, что при схеме соединения обмоток статора «звезда» фазные и линейные токи равны, а фазное напряжение в раз меньше линейного; при схеме «треугольник» — наоборот: фазные и линейные напряжения равны, а фазный ток в раз меньше линейного. При этом номинальные токи и напряжения асинхронного двигателя всегда линейные. Сказанное выше относится также и к трансформаторам.

Источник