Решение задачи о назначениях с помощью Excel
Задача о назначениях является типичным примером оптимального принятия управленческих решений. Эта задача позволяет распределить объекты из некоторого множества по группе субъектов из другого множества и это распределение должно соответствовать оптимальности одного или нескольких итоговых показателей.
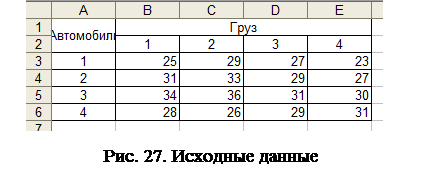
Постановка задачи. Пусть на предприятии имеется 4 разных грузовых автомобиля. Необходимо доставить разный товар в 4 разных района области. Общие затраты на перевозку каждого вида товара каждым автомобилем известны. Требуется так выбрать для каждого вида товара автомобиль так, чтобы суммарные затраты на перевозку были минимальными.
Исходные данные представлены на рис. 27.
 |
Математическая модель задачи о назначениях имеет следующий вид.
1. Переменные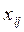 
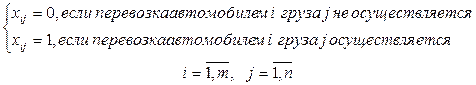
принимают два значения:
(17)
2. Все переменные задачи – неотрицательные значения и целые числа:
(18)
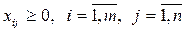
Также, так как каждый автомобиль может выполнять доставку только одного груза и весь груз должен быть доставлен, переменные должны отвечать следующим ограничениям:
(19)
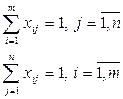
Это условие означает, что выбор вариантов доставки должен быть таким, чтобы в таблице, представляющей решение задачи, было по одной единице в каждой строке и в каждом столбце. Остальные элементы должны равняться нулю.
3. Целевая функция, направленная на минимум суммарных затрат:
(19)
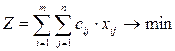
Таким образом, алгоритм решения задачи о назначениях такой же, как у классической транспортной задачи (практическая работа №2).
Рассмотрим решение данной задачи.
На рис. 28 показано поле для решения задачи о назначениях.
 |
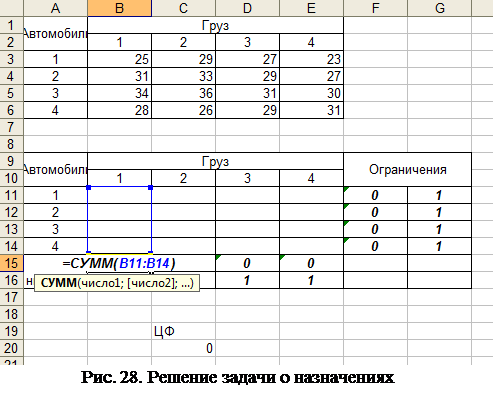Целевая функция рассчитывается как сумма произведений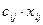 
:
 |
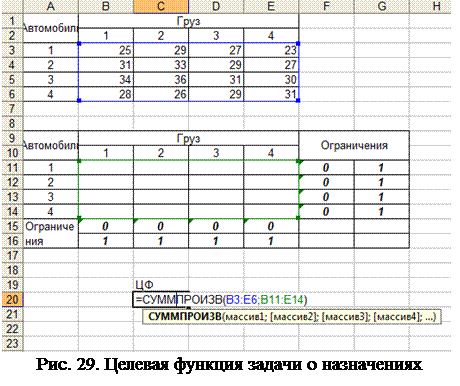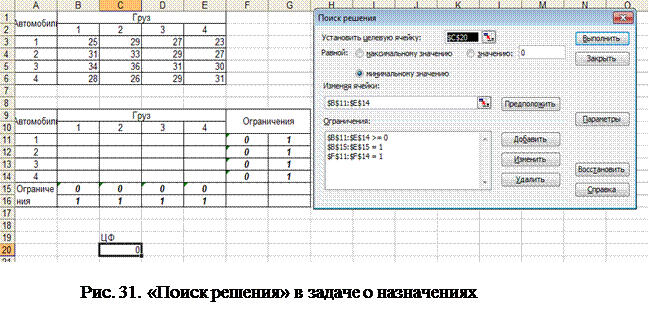
«Поиск решения» производится следующим образом (рис. 30)
 |
В меню «Параметры» «Поиска решения» необходимо установить «Линейная модель». Результаты расчетов приведены на рис. 32.
Методика решения задачи о назначении в MS EXCEL
Для решения задачи о назначении с помощью программы MS Excel необходимо задать конкретные значения параметрам. Для определенности рассмотрим вариант задачи о назначении в форме минимизации общих затрат на выполнение работ. В этом случае в качестве кандидатов рассмотрим сотрудников некоторой фирмы: Андреев, Бубнов, Васильев, Григорьев и Дмитриев, а в качестве работ – вакантные должности в этой фирме: менеджер, программист, бизнес-аналитик, маркетолог и руководитель проектов. Затраты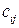 
на замещение должностей кандидатами, связанные с необходимостью их предварительного обучения и стажировки, заданы в форме следующей таблицы.
Затраты на замещение должностей кандидатами, тыс. тнг.
| Андреев | Бубнов | Васильев | Григорьев | Дмитриев |
| Менеджер | ||||
| Программист | ||||
| Бизнес-аналитик | ||||
| Маркетолог | ||||
| Руководитель проектов |
Соответствующая математическая постановка рассматриваемой задачи о назначении может быть записана в следующем виде:
(2.14)
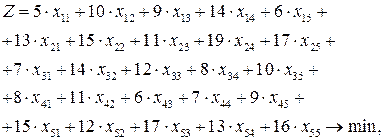
где множество допустимых альтернатив формируется следующей системой ограничений типа равенств:
(2.15)
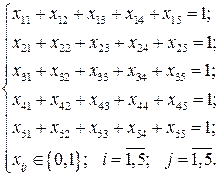
Первые 5 ограничений данной задачи соответствуют общему ограничению (2.11), следующие 5 ограничений – общему ограничению (2.12), а последнее ограничение – общему ограничению (2.13).
Для решения сформулированной задачи о назначении с помощью программы MS Excel выполним следующие подготовительные действия:
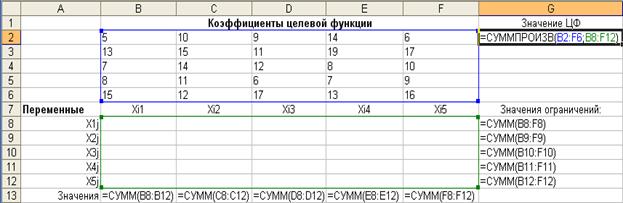
1. Внесем необходимые надписи в ячейки A7:A13, B1, G1, B7:G7,как это изображено на рис. 2.7. Следует отметить, что конкретное содержание этих надписей не оказывает никакого влияния на решение рассматриваемой задачи о назначении.
2. В ячейки B2:F6введем значения коэффициентов целевой функции (см. табл. 2.4).
3. В ячейку G2введем формулу: =СУММПРОИЗВ(B2:F6;B8:F12), которая представляет целевую функцию Z.
4. В ячейку G8введем формулу: =СУММ(B8:F8), которая представляет первое ограничение из приведенной системы ограничений.
5. Скопируем формулу, введенную в ячейку G8, в ячейки G9:G12.
6.В ячейку B13введем формулу: =СУММ(B8:B12), которая представляет шестое ограничение из приведенной системы ограничений.
7.Скопируем формулу, введенную в ячейку B13,в ячейкиC13:F13.
Внешний вид рабочего листа MS Office Excel 2003 с исходными данными для решения задачи о назначении представлен на рис. 2.7.
Рис. 2.7. Исходные данные для решения задачи о назначении
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню: Сервис Þ Поиск решения.
После появления диалогового окна Поиск решенияследует выполнить следующие действия:
1.В поле с именем Установить целевую ячейку:ввести абсолютный
2.Для группы Равной:выбрать вариант поиска решения – минимальному значению.
4.Задать первую группу ограничений, соответствующих первым 5 базовым ограничениям исходной постановки решаемой задачи о назначении. С этой целью выполнить следующие действия:
î в исходном диалоговом окне Поиск решениянажать кнопку с надписью Добавить;
îв появившемся дополнительном окне выбрать диапазон ячеек $G$8:$G$12,который должен отобразиться в поле с именем Ссылка на ячейку;
îв качестве знака ограничения из выпадающего списка выбрать равенство «=»;
îв качестве значения правой части ограничения ввести с клавиатуры число 1;
îдля добавления первой группы ограничений в дополнительном окне нажать кнопку с надписью Добавить.
5.Задать вторую группу ограничений, соответствующих оставшимся 5 базовым ограничениям исходной постановки решаемой задачи о назначении. С этой целью выполнить следующие действия:
îв исходном диалоговом окне Поиск решениянажать кнопку с надписью Добавить.
îв появившемся дополнительном окне выбрать диапазон ячеек $B$13:$F$13, который должен отобразиться в поле с именем Ссылка на ячейку;
îв качестве знака ограничения из выпадающего списка выбрать равенство «=»;
îв качестве значения правой части ограничения ввести с клавиатуры число 1;
îдля добавления второй группы ограничений в дополнительном окне нажать кнопку с надписью Добавить.
6.Добавить последнее ограничение на булевы значения переменных задачи. С этой целью выполнить следующие действия:
îв исходном диалоговом окне Поиск решениянажать кнопку с надписью Добавить;
îв появившемся дополнительном окне выбрать диапазон ячеек $B$8:$F$12,который должен отобразиться в поле с именем Ссылка на ячейку;
î в качестве знака ограничения из выпадающего списка выбрать строку «двоичн»;
îв качестве значения правой части ограничения в поле с именем Ограничение:оставить без изменения вставленное программой значение «двоичное»;
î для добавления в дополнительном окне нажать кнопку с надписью Добавить.
7.В окне дополнительных параметров поиска решения выбрать отметку Линейная модельиНеотрицательные значения.
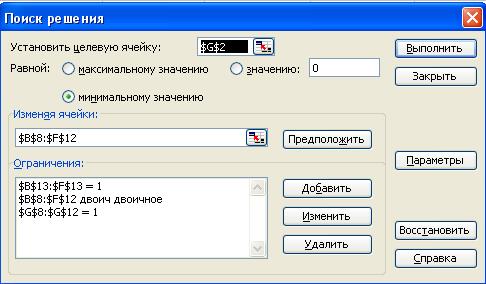
Общий вид диалогового окна спецификации параметров мастера поиска решения представлен на рис. 2.8.
Рис. 2.8.Параметры мастера поиска решения и базовые ограничения
для задачи о назначении
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить.После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, приведенный на рис. 2.9.
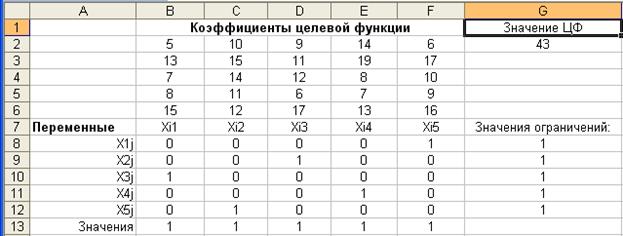
Рис. 2.9.Результат количественного решения задачи о назначении
Результатом решения рассматриваемой задачи о назначении являются найденные оптимальные значения переменных: х15 = 1, х23 = 1, х31 = 1, х44 = 1, х52 =1, остальные переменные равны 0. Найденному оптимальному решению соответствует минимальное значение целевой функции ¦opt = 43.
Анализ найденного решения показывает, что при замещении вакантных должностей в рассматриваемой фирме следует на должность менеджера назначить сотрудника Дмитриева, на должность программиста – Васильева, на должность бизнес-аналитика – Андреева, на должность маркетолога – Григорьева и, наконец, на должность руководителя проектов – Бубнова. При этом общие затраты на обучение и стажировку сотрудников составят 43 тыс. тенге.
Большинство целочисленных и комбинаторных типов задач, таких, как задача с неделимостями, задача коммивояжера, задача календарного планирования, принадлежит к разряду так называемых трудно решаемых. Это означает, что вычислительная сложность алгоритма их точного решения – зависимость числа элементарных операций (операций сложения или сравнения), необходимых для получения точного решения, от размерности задачи n – является экспоненциальной (порядка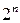 
), т.е. сравнимой по трудоемкости с полным перебором вариантов. В качестве n, например, для задачи с неделимостями служит число целочисленных переменных и число ограничений, для задачи коммивояжера – число городов (или узлов графа маршрутов), для задачи календарного планирования – число деталей и число станков. Такие задачи называют еще NP-трудными или NP-полными. Получение их точного решения не может быть гарантировано, хотя для некоторых задач данного типа существует эффективные методы, позволяющие находить точное решение даже при больших размерностях. Примером таких задач служит задача о ранце с булевыми переменными.
Дата добавления: 2015-11-18 ; просмотров: 3787 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Как решить транспортную задачу в Excel
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.
Решение транспортной задачи в Excel с примером и описанием
Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 | |
Задача: минимизировать транспортные расходы по перевозке продукции.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Реферат: Решение транспортных задач в Excel
| Название: Решение транспортных задач в Excel Раздел: Рефераты по информатике Тип: реферат Добавлен 10:10:42 22 июня 2011 Похожие работы Просмотров: 1305 Комментариев: 19 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать |
Рисунок 1 – Объемы спроса и предложения
Таблица 1 – Кратчайшие расстояния, км
Средняя стоимость перевозки 1 мешка с цементом на 1 км составляет 5 рублей. В результате получаем, представленную в таблице 2, стоимость перевозок по каждому маршруту.
Стоимость перезозки, руб
1.1 Математическая постановка задачи
 |
В исследовании операций под транспортной задачей обычно понимают задачу выбора плана перевозок некоторого товара (изделий, груза) от m источников (пунктов производства, поставщиков) к n стокам (станциям назначения, пунктам сбыта), обеспечивающего минимальные транспортные затраты. При этом предполагают, что:
г) суммарная мощность всех источников равна суммарной мощности всех стоков, т.е.
Далее под объемом товара будем понимать его количество в фиксированных единицах измерения.
 |
Рисунок 3 – Представление транспортной задачи в виде сети 1.2 Решение задачи в среде Excel Используя меню СервисÞПоиск решения открываем диалоговое окно Поиск решения, в котором устанавливаем целевую ячейку равной минимальному значению, определяем диапазон изменяемых ячеек и ограничения и запускаем процедуру вычисления, щелкнув по кнопке Выполнить.
В Excel несбалансированная транспортная задача решается путем изменения ограничений по спросу (если спрос превышает предложение) или по предложению (если предложение превышает спрос). Таблица 9 – План оптимального закрепления
Потребительский спрос бассейна и школы удовлетворены полностью. На складе Волжского района остается не вывезенным 300 мешков, на Ленинском складе – 250 мешков. Общая стоимость перевозки составляет 53500 условных единств. Транспортная задача с промежуточными пунктамиВ транспортной сети, показанной на рисунке 2, осуществляются перевозки груза из пунктов 1 и 2 в пункты 5 и 6 через транзитные пункты 3 и 4. Стоимость перевозки единицы груза между пунктами показана в таблице 3. Предложение пунктов 1, 2 (П1 и П2) и спрос пунктов 5,6 (С5 и С6) выбирается соответственно из таблиц 4 и 5. Построить транспортную модель с промежуточными пунктами.
Рисунок 2 – Схема транспортной сети Таблица 3 – Стоимость перевозки единицы груза между |
