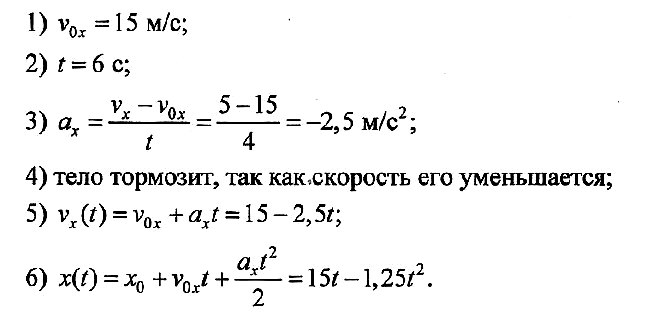За время в течение которого автомобиль движущийся с постоянным ускорением проехал 80

За время в течение которого автомобиль движущийся с постоянным ускорением проехал 80

Автомобиль, движущийся в начальный момент времени со скоростью м/с, начал торможение с постоянным ускорением м/с За t секунд после начала торможения он прошёл путь (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 80 метров. Ответ выразите в секундах.

Это задание ещё не решено, приводим решение прототипа.

Найдем, за какое время, прошедшее от момента начала торможения, автомобиль проедет 30 метров:

Значит, через 2 секунды после начала торможения автомобиль проедет 30 метров.

Примечание о выборе корня.

Формула описывает движение автомобиля от начала торможения до полной остановки. Моменту остановки соответствует наибольший пройденный путь. Наибольшее значение квадратного трехчлена достигается в точке в нашем случае Следовательно, через 4 секунды после начала движения автомобиль остановится. Поэтому больший корень уравнения не подходит по смыслу задачи.

Если бы автомобиль после остановки продолжил движение в соответствии с заданной формулой, он поехал бы назад, увеличивая скорость. В некоторый момент времени автомобиль вновь оказался бы на заданном расстоянии от начального положения. Этот момент определяется большим корнем решенного уравнения.

Для читателей, закончивших 9 класс, приведем объяснение в общем виде, опираясь на знания курса физики. При равноускоренном движении Из формулы скорости следует, что при торможении скорость тела достигает нуля в момент времени Поэтому при решении задач на пройденный при торможении путь допустимыми являются моменты времени, не большие t₀.

Рекомендуем сравнить это задание с заданиями 27961 и 27962.

Источник

За время в течение которого автомобиль движущийся с постоянным ускорением проехал 80

Автомобиль, движущийся в начальный момент времени со скоростью м/с, начал торможение с постоянным ускорением м/с За t секунд после начала торможения он прошел путь (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 112 метров. Ответ выразите в секундах.

Значит, через 7 секунд после начала торможения автомобиль проедет 112 метров.

Значит, через 4 секунды после начала торможения автомобиль проедет 60 метров.

Значит, через 5 секунд после начала торможения автомобиль проедет 60 метров.

Автомобиль, движущийся в начальный момент времени со скоростью м/с, начал торможение с постоянным ускорением м/с За t секунд после начала торможения он прошёл путь (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 90 метров. Ответ выразите в секундах.

Это задание ещё не решено, приводим решение прототипа.

Найдем, за какое время, прошедшее от момента начала торможения, автомобиль проедет 30 метров:

Значит, через 2 секунды после начала торможения автомобиль проедет 30 метров.

Примечание о выборе корня.

Формула описывает движение автомобиля от начала торможения до полной остановки. Моменту остановки соответствует наибольший пройденный путь. Наибольшее значение квадратного трехчлена достигается в точке в нашем случае Следовательно, через 4 секунды после начала движения автомобиль остановится. Поэтому больший корень уравнения не подходит по смыслу задачи.

Если бы автомобиль после остановки продолжил движение в соответствии с заданной формулой, он поехал бы назад, увеличивая скорость. В некоторый момент времени автомобиль вновь оказался бы на заданном расстоянии от начального положения. Этот момент определяется большим корнем решенного уравнения.

Для читателей, закончивших 9 класс, приведем объяснение в общем виде, опираясь на знания курса физики. При равноускоренном движении Из формулы скорости следует, что при торможении скорость тела достигает нуля в момент времени Поэтому при решении задач на пройденный при торможении путь допустимыми являются моменты времени, не большие t₀.

Рекомендуем сравнить это задание с заданиями 27961 и 27962.

Автомобиль, движущийся в начальный момент времени со скоростью м/с, начал торможение с постоянным ускорением м/с За t секунд после начала торможения он прошёл путь (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.

Это задание ещё не решено, приводим решение прототипа.

Найдем, за какое время, прошедшее от момента начала торможения, автомобиль проедет 30 метров:

Значит, через 2 секунды после начала торможения автомобиль проедет 30 метров.

Примечание о выборе корня.

Формула описывает движение автомобиля от начала торможения до полной остановки. Моменту остановки соответствует наибольший пройденный путь. Наибольшее значение квадратного трехчлена достигается в точке в нашем случае Следовательно, через 4 секунды после начала движения автомобиль остановится. Поэтому больший корень уравнения не подходит по смыслу задачи.

Если бы автомобиль после остановки продолжил движение в соответствии с заданной формулой, он поехал бы назад, увеличивая скорость. В некоторый момент времени автомобиль вновь оказался бы на заданном расстоянии от начального положения. Этот момент определяется большим корнем решенного уравнения.

Для читателей, закончивших 9 класс, приведем объяснение в общем виде, опираясь на знания курса физики. При равноускоренном движении Из формулы скорости следует, что при торможении скорость тела достигает нуля в момент времени Поэтому при решении задач на пройденный при торможении путь допустимыми являются моменты времени, не большие t₀.

Рекомендуем сравнить это задание с заданиями 27961 и 27962.

Автомобиль, движущийся в начальный момент времени со скоростью м/с, начал торможение с постоянным ускорением м/с За t секунд после начала торможения он прошёл путь (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 60 метров. Ответ выразите в секундах.

Это задание ещё не решено, приводим решение прототипа.

Найдем, за какое время, прошедшее от момента начала торможения, автомобиль проедет 30 метров:

Значит, через 2 секунды после начала торможения автомобиль проедет 30 метров.

Примечание о выборе корня.

Формула описывает движение автомобиля от начала торможения до полной остановки. Моменту остановки соответствует наибольший пройденный путь. Наибольшее значение квадратного трехчлена достигается в точке в нашем случае Следовательно, через 4 секунды после начала движения автомобиль остановится. Поэтому больший корень уравнения не подходит по смыслу задачи.

Если бы автомобиль после остановки продолжил движение в соответствии с заданной формулой, он поехал бы назад, увеличивая скорость. В некоторый момент времени автомобиль вновь оказался бы на заданном расстоянии от начального положения. Этот момент определяется большим корнем решенного уравнения.

Для читателей, закончивших 9 класс, приведем объяснение в общем виде, опираясь на знания курса физики. При равноускоренном движении Из формулы скорости следует, что при торможении скорость тела достигает нуля в момент времени Поэтому при решении задач на пройденный при торможении путь допустимыми являются моменты времени, не большие t₀.

Рекомендуем сравнить это задание с заданиями 27961 и 27962.

Автомобиль, движущийся в начальный момент времени со скоростью м/с, начал торможение с постоянным ускорением м/с За t секунд после начала торможения он прошёл путь (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 36 метров. Ответ выразите в секундах.

Это задание ещё не решено, приводим решение прототипа.

Найдем, за какое время, прошедшее от момента начала торможения, автомобиль проедет 30 метров:

Значит, через 2 секунды после начала торможения автомобиль проедет 30 метров.

Примечание о выборе корня.

Формула описывает движение автомобиля от начала торможения до полной остановки. Моменту остановки соответствует наибольший пройденный путь. Наибольшее значение квадратного трехчлена достигается в точке в нашем случае Следовательно, через 4 секунды после начала движения автомобиль остановится. Поэтому больший корень уравнения не подходит по смыслу задачи.

Если бы автомобиль после остановки продолжил движение в соответствии с заданной формулой, он поехал бы назад, увеличивая скорость. В некоторый момент времени автомобиль вновь оказался бы на заданном расстоянии от начального положения. Этот момент определяется большим корнем решенного уравнения.

Для читателей, закончивших 9 класс, приведем объяснение в общем виде, опираясь на знания курса физики. При равноускоренном движении Из формулы скорости следует, что при торможении скорость тела достигает нуля в момент времени Поэтому при решении задач на пройденный при торможении путь допустимыми являются моменты времени, не большие t₀.

Рекомендуем сравнить это задание с заданиями 27961 и 27962.

Источник

За время в течение которого автомобиль движущийся с постоянным ускорением проехал 80

Автомобиль, движущийся в начальный момент времени со скоростью м/с, начал торможение с постоянным ускорением м/с За t секунд после начала торможения он прошёл путь (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 36 метров. Ответ выразите в секундах.

Это задание ещё не решено, приводим решение прототипа.

Найдем, за какое время, прошедшее от момента начала торможения, автомобиль проедет 30 метров:

Значит, через 2 секунды после начала торможения автомобиль проедет 30 метров.

Примечание о выборе корня.

Формула описывает движение автомобиля от начала торможения до полной остановки. Моменту остановки соответствует наибольший пройденный путь. Наибольшее значение квадратного трехчлена достигается в точке в нашем случае Следовательно, через 4 секунды после начала движения автомобиль остановится. Поэтому больший корень уравнения не подходит по смыслу задачи.

Если бы автомобиль после остановки продолжил движение в соответствии с заданной формулой, он поехал бы назад, увеличивая скорость. В некоторый момент времени автомобиль вновь оказался бы на заданном расстоянии от начального положения. Этот момент определяется большим корнем решенного уравнения.

Для читателей, закончивших 9 класс, приведем объяснение в общем виде, опираясь на знания курса физики. При равноускоренном движении Из формулы скорости следует, что при торможении скорость тела достигает нуля в момент времени Поэтому при решении задач на пройденный при торможении путь допустимыми являются моменты времени, не большие t₀.

Рекомендуем сравнить это задание с заданиями 27961 и 27962.

Источник

За время в течение которого автомобиль движущийся с постоянным ускорением проехал 80

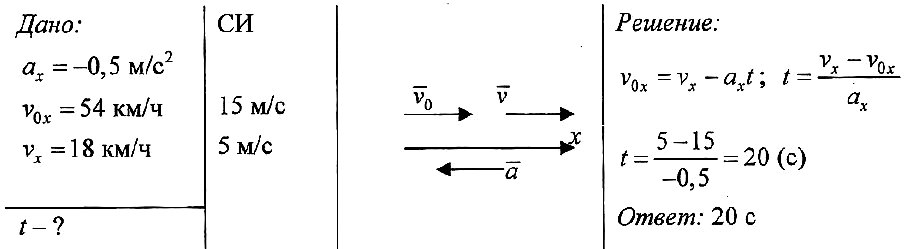
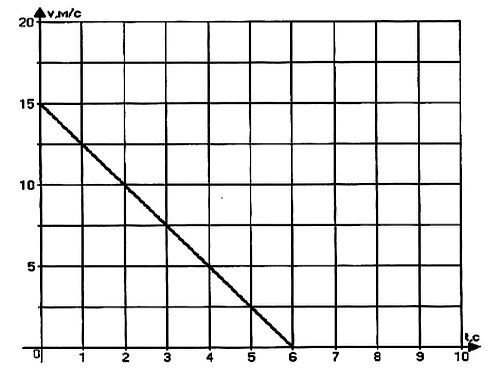
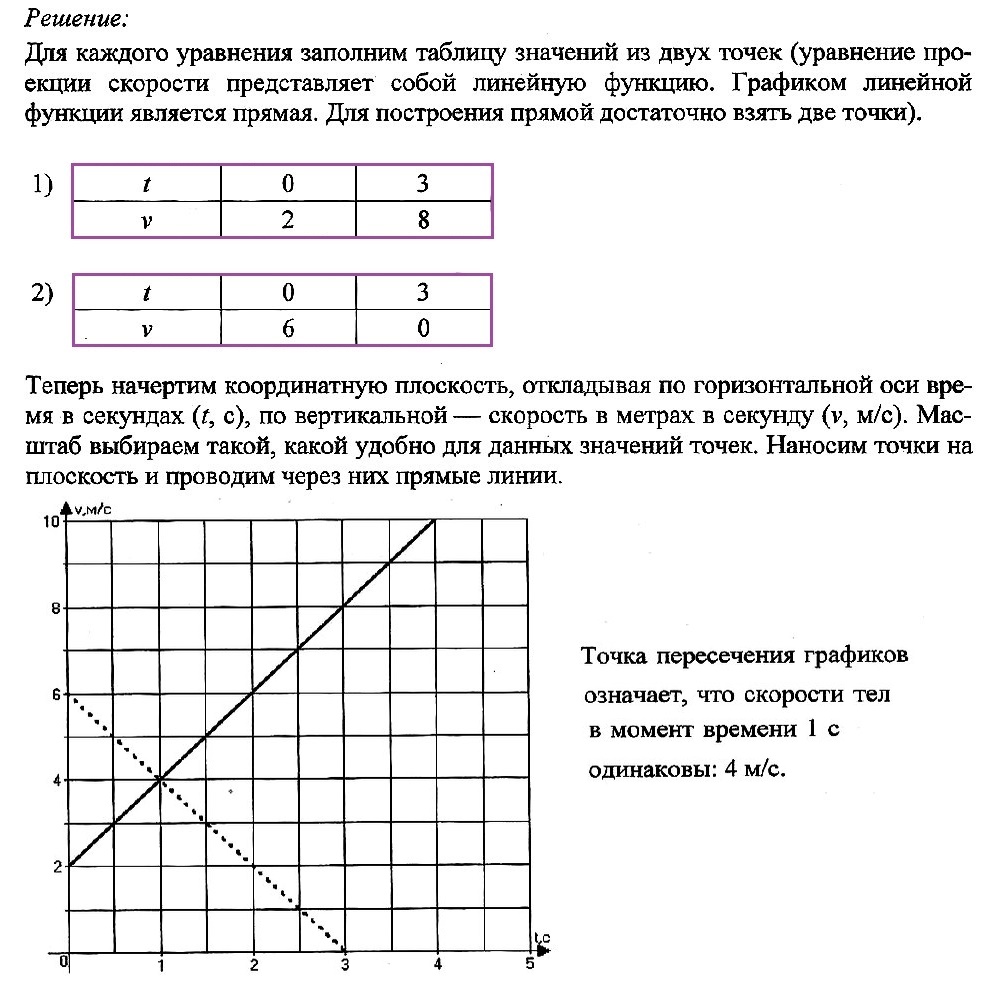
Задача № 3. По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).

Решение:

Задача № 4. Движение двух тел задано уравнениями проекции скорости:
v_1x(t) = 2 + 2t
v_2x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?

Решение:

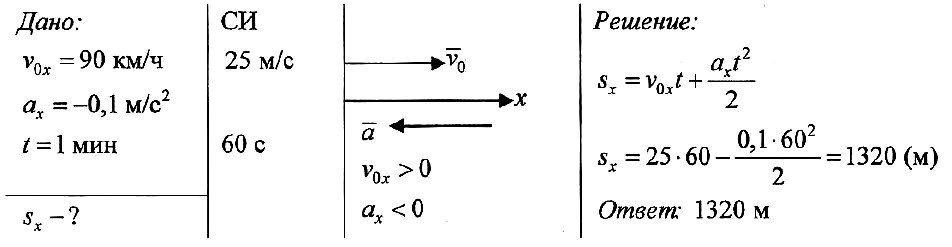
Задача № 7. Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с 2 в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).

Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.

Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:

29 Комментарии

Спасибо за альтернативную точку зрения, не указанную в школьных учебниках физики. Надеюсь, это поможет учащимся расширить свой кругозор в области физики.

Ускорение — это вектор, а он отрицательным быть не может. Но вот проекция ускорения очень даже может быть отрицательной. И, прямо скажем, я не пойму что Вы тут написали, но попахивает каким-то бредом. Хотя бы потому, что at — это приращение скорости, а средняя скорость — это перемещение деленное на время движения, или путь на время движения, если интересует средняя ПУТЕВАЯ скорость. Деление же на 2, в уравнении движения возникает из-за правил интегрирования, которые говорят о том, что интеграл at по dt равен 0.5at^2/

Тело движется прямолинейно под действием постоянной силы 12 Н, при этом зависимость координаты тела от времени имеет вид: (м). Определить: массу тела; импульс тела в момент времени t = 2 c ; среднюю скорость за промежуток времени от t1 = 0 c до t2 = 2 c.

S/tt=F/m. S=? Тело двигалось,или стояло?

….мощность мотора при условиях в задаче. (вес машины…1200 кг)
..машина имела ускорение 4 м/сс.. (для машины-«приличное» ускорение..) F/1200=4 сек.сек. F=4800 кг м./сек. Это=64 л.с. при 100% КПД
КПД ДВС=16 %. 64*6,25=400 л.с. (есть такие моторы. Правда, вес ТАКИХ машин 2,5-3 тонны…) Вот пример «теории и практики». А если вес машины …2650 кг., то мотор должен быть: 4*2650/75*6,25=883 л.с.

Определить тормозную путь,если известны начальная скорость 30 м/сек и замедление 6 м/сек2

V кон.=2at. 30=2*6*t. t=2,5 c. S=att. 6*2,5*2,5. S=37,5 м.

В последней задаче: t= V ср./ a. Vср.=15 м/с. t=15/6=2,5 секунды (быстрее свободного падения…) S=att. 6*2,5*2/5=37,5 м.

(…напутал в решении…)
При «ускорении» 19 м/сс, скорость через 30 сек. будет: Vкон.=2at. 2*19*30. V кон.=1140 м/с. (4104 км/час)

во второй задаче: V нач.=25 м/с. а=0,1 м/сс. t=60 c. S=? (давать надо одно: или «ускорение», или «время»)
решение: S=V ср.*t. 12,5*60=750 м. «ускорение»= V ср./t. 12,5/60. t=0,2 м/сс.
При «а»=0,1 м/сс. t=Vср./a. 12,5/0,1=125 секунд.
S при а=0,2 м/сс. S=att. 0,208*60*60=750 м. (и при разгоне, и при торможении)
S при а=0,1 м/сс. S=att. 0,1/125*125. S=1562,5 м. (и при разгоне. и при торможении)

задача № 9
V нач.=х. V кон.=5х. V ср.=3х. t=2c. S=18 м. V ср.=9 м. х=9/3=3 м/с. V кон.=15 м/с.
a=S/tt=Vср./t a=18/4=9/2=4,5 м/сс
ПРОВЕРКА: S=att. 4,5*2*2=18 м.
Проверка (по Вашему решению): a=6 м/сс. S=att/2. 6*2*2/2=12 м (?)

У Вас не получается, потому что Вы проверяете ответ по своей формуле. Правильная формула проекции перемещения указана в начале статьи и в самой задаче!

Вот такие «анонимы» в средневековье … всех, кто думал не так, как «принято». (текст изменен модератором сайта)

Во второй задаче некорректная формулировка. По факту, даны избыточные данные. «Тормозной путь» соответствует расстоянию до полной остановки, то есть такое понятие подразумевает конечную скорость, равную нулю. А по заданным числам конечная скорость будет равна v0 — a * t = 25 — 0.1*60 = 19 м/c.

Возможно, конкретно в это задаче автор подразумевал под тормозным путём участок, на котором поезд замедлял движение, при этом не до полной остановки. Меня это тоже вначале сбило с толку.

В 11-й задаче проще использовать формулу a = (V-Vo) / t

Даша! V конечная (при равно-ускоренном движении и одной из скоростей=0 ) есть 2at. СРЕДНЯЯ скорость (25+0)/2=12,5 м/с. С такой СРЕДНЕЙ скоростью поезд за минуту (60 сек) пройдёт: 12,5*60=750 м.
Если задачу решать через «а», то t=12,5/0,1=125 секунд. S=V ср.*t. 12,5*125=1562,5 м.
Если поезд (по условию задачи) прошёл 750 м. (до остановки), то его ЗАМЕДЛЕНИЕ скорости (-«а»): S=att 750/60/60. а=0,2 м/сс.
Вывод: давать в условии задачи одно: или «а», или t

С точки зрения физики торможение — это тоже ускорение, только с обратным знаком. Поменяли условие задачи № 2, чтобы не было двусмысленности.

всем доброго времени.
Очень е силен в физике последние лет 25, по этой причине прошу помочь в решении некой задачи!
Дано начальная скорость = 10 м/с.
Вопрос сможет ли тело долететь до высоты 4 м и если сможет то с какой скоростью. Да, полет вертикальный!
На мой взгляд в даны не все условия, но могу и ошибаться.
Спасибо.

Такие задачи рассматриваются в разделе «Задачи на свободное падение» https://uchitel.pro/задачи-на-свободное-падение/

Добавить комментарий Отменить ответ

Конспекты по физике:

7 класс

8 класс

9 класс

10-11 классы

Найти конспект:

О проекте

Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Возрастная категория: 12+

(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!

Источник