Сколько по времени ехать 100 километров?
Смотря с какой скоростью передвигаться, ведь от этого в первую очередь зависит время, за которое преодолеете такое расстояние. К примеру, можно ехать со скоростью сто километров в час, в этом случае сто километров проедете как раз за один час. Если ехать ещё быстрее, к примеру, в сто пятьдесят километров в час, то будет ещё быстрее, а если ехать медленно, к примеру пятьдесят километров в час, то времени на поездку уйдёт больше, уже ровно два часа.
Все зависит от того, на чем вы едете и где вы едете.
Давайте рассмотрим, если вы передвигаетесь на автомобиле по хорошей трассе, где нет населенных пунктов, то средняя скорость будет составлять 90-100 км/час (а значит, доберетесь за час). Если будут ремонты дороги, населенные пункты в виде деревень, дач, то время в пути будет составлять около 1,5 часов (так как на этих участках действует ограничение скорости).
Теперь рассмотрим, что эти 100 км вам надо проехать по городу, где есть светофоры (исключим пробки), в этом случае, время может быть от 2 до 3 часов (а то и больше, смотря, как вам повезет со светофорами).
Допустим, вы передвигаетесь на велосипеде. Скорость передвижения значительно меньше и зависит от самого велосипедиста. Берем среднюю скорость — 20-25 км/час, а значит, 100 км велосипедист в среднем проедет за 4 часа.
Проехать 100 километров на машине можно за 2 часа, поскольку в черте города средняя скорость — 50 км в час. Если на велосипеде или на сигвее, то при скорости 20 км в час, расстояние в 100 километров можно преодолеть за 5-6 часов.
Вы можете войти или зарегистрироваться, чтобы добавить ответ и получить бонус.
Сколько реально тормозит ваш автомобиль?
А за сколько реально тормозит ваш автомобиль на скорости 60, 80 или 100 км в час? Многие автовладельцы не смогут с ходу ответить на этот вопрос. А вот за сколько до сотни разгоняется машина известно многим.
Тормозной путь современного автомобиля по сухому асфальту при скорости 60 км в час составляет 12 метров.
Запомним эту цифру. Теперь, чтобы перенести ногу с педали газа на педаль тормоза с полным ее выжимом подготовленному человеку нужно пол секунды. Это еще 8 метров. Суммируем 8+12 и получаем 20 метров тормозного пути.
Время принятия решения на торможение у водителя с опытом вождения – 0.8 секунды, а у не опытного – больше 1 секунды. Это еще 16 – 19 метров.
В результате получается 32 – 39 метров остановочного тормозного пути. И не забываем, это только при скорости 60 км в час.
При скорости 100 км в час машина, у опытного водителя, полностью остановится при экстренном торможении через 42 м. А начинающие водителя часто не укладываются и в 60 м.
Поэтому важно научиться правильно работать с педалью тормоза и понимать, как функционирует вся тормозная система.
Важно знать, что в переднеприводном авто тормозят не только передние колеса, и что в тормозах работает специальная жидкость.
Нужно банально понимать, за сколько ваше авто останавливается. Переобулись? Тогда обязательно проверьте, как тормозит машина после этой процедуры. Всем удачи.
Расход топлива: 50 км/ч против 100 км/ч.
Изучая технические данные автомобилей, мы привыкли видеть вполне обычные результаты показаний расхода топлива в городе и на шоссе. При этом, расход топлива в городе обычно выше загородного, ведь за городом не так много знаков, перекрестков и светофоров. Машина обычно едет с равномерной высокой скоростью.
В своей записи Замер реального среднего расхода топлива он, будучи простым программистом, пытался разъяснить как следует ездить максимально выгодно. И что самое интересное, никто, кроме меня, даже не обратил на это внимание. Вот цитаты оттуда:
Идеальный случай для топливной экономичности — равномерное перемещение по прямой линии на оборотах максимального крутящего момента на скорости 90-100 км/ч. Почему? Потому что именно на оборотах МКМ двигателю проще всего преодолевать силы сопротивления. А любое, даже самое незначительное ускорение приводит к серьезному увеличению мгновенного расхода топлива. И именно на 100 км/ч начинается серьезное влияние аэродинамики на сопротивление движению.
Я совсем не простой, и тем более не программист, но чувствую, что здесь есть подвох. Не могу похвастаться большими цифрами своего водительского стажа, но в последние годы вожу машину регулярно и слежу за расходом топлива. Поэтому примерно знаю как и в каких режимах автомобиль использует мощность и сколько он на это тратит жидкого запаса энергии.
Дальше же идет еще интереснее:
Допустим, что наш абстрактный автомобиль, двигаясь на 2000 об/мин со скоростью 100 км/ч на 5 передаче потребляет 6 литров топлива на 100 км. Это тоже самое, что и 6 литров топлива в час. Допустим, что на третьей передаче, на тех же 2000 об/мин, наш автомобиль движется со скоростью 50 км/ч. При этом снижается сопротивление воздуха, да и большее передаточное число позволяет легче «крутить педали». И наш расход падает до 4 литров в час. Но 100 км мы преодолеем за 2 часа, потратив на это уже 8 литров топлива. Вот такая простая арифметика
Меня, будучи водителем легкового автомобиля с вариатором, сразу смутил выбор передачи на указанных скоростях. Зная свои автомобили с вариатором, я прекрасно понимаю, что в движении на скорости 50 км/ч и 100 км/ч они выбирают оптимальное передаточное число трансмиссии и количество оборотов в минуту двигателя, чтобы удерживать тот равномерный курс движения. Причем на этих скоростях обороты двигателя, судя по тахометру, различаются значительно. Единственное, что я не могу сказать о передаточном числе, так как селектор вариатора находится в положении D и только. Возможно, мастерство redzub подсказывает ему выбирать различное передаточное число на его МКПП, но придерживаться одних оборотов двигателя его автомобиля.
Но можно приводить формулы и расчеты, а расход — всё равно будет величиной не постоянной. Потому что невозможно 2 раза проехать по одной и той же траектории с точностью до миллиметра, не говоря уже о том, чтобы выдержать на этой траектории одинаковые значения ускорений, массы автомобиля и сил сопротивления (банальный ветер дует всегда в разные стороны, не говоря уже об интенсивности работы климат-контроля).
Не поверив словам цитат, указанных выше, я решил проехать по одной дороге, с одинаковыми условиями движения но с различной скоростью: 50 км/ч и 100 км/ч.
Для этого я выбрал новый автомобиль линейки Mitsubishi под названием Outlander Sport ES с вариатором. Пробег на момент начала тестирования равнялся 6900 км. То есть машина, можно сказать, вот только что после обкатки. Никаких модификаций в автомобиле не проводилось, кроме установленных брызговиков, но они будут влиять на топливную экономичность в обоих случаях.
Сразу перед тестом я заправился бензином под пробку, но проверять реальный расход топлива и по показаниям бортового компьютера я не стал. Тем не менее, я сравниваю показания «приборки» и по «чекам» после всех заправок.
Как и говорит redzub : «Доверять бортовому компьютеру тоже сильно не стоит — он может давать погрешность«.
Тем не менее, в одних и тех же условиях можно положиться и на бортовой компьютер, особенно зная его постоянную ошибку.
Итак, примерно предположив, что ранним воскресным утром я могу проехать по одному и тому же участку дороги дважды на скоростях 50 км/ч и 100 км/ч, никому особо не мешая, я выбрался к 6 утра за 130 км от дома в пустыню Мохаве на шоссе номер 14. Так как мне нужна была помощь, в ней мне не отказала жена (надо было встать в 3.30 утра, вы бы смогли ради этого?)
Первоначальный план состоял из: на скорости 31 миля/ч (50 км/ч) проехать в одну сторону 31 милю (50 км) и вернуться. Затем преодолеть тот же маршрут, но уже на скорости 62 миль/ч (100 км/ч).
Но проехав в одну сторону только 18 миль (29 км), я решил возвращаться, так как количество автомобилей росло, а дорожные полицейские, скорей всего начали просыпаться. По пути назад я увидел патруль, едущий навстречу. Поглядывая в зеркало заднего вида, я стал следить, если полиция не решила меня остановить. Стоит сказать, я ехал 31 миля/ч на дороге с ограничением 65 миль/ч, то есть «сильно мешал» попутному движению, что значит — нарушал правило. Проехав в итоге 13 миль обратно, я видел, что примерно за 500 метров позади меня мчится патруль с включенными проблесковыми маячками. Я «топнул» до 65 миль/ч и на этом тест на скорости 50 км/ч закончился. Патруль отстал.
Вернувшись в исходную точку, я обнулил временные (A) показания бортового компьютера, разогнался до 62 миль/ч (100 км/ч) и снова зафиксировал круиз-контроль. В этот раз можно было ехать не переживая и спокойно фиксировать данные.
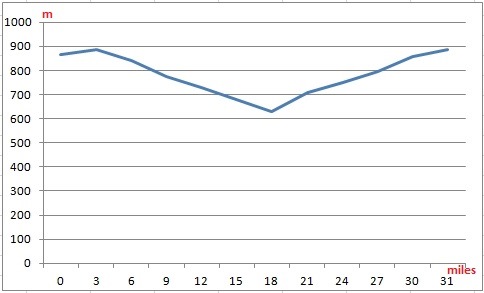
Так мы с женой фиксировали показания расхода топлива (в MPG) каждый 3 пройденных мили. При этом фиксировали по навигатору высоту над уровнем моря. Для общей картины еще записывали температуру воздуха. На второй тест температура выросла по всем точкам примерно на 1 градус Цельсия.
Стоит еще добавить, что был сильный боковой ветер. Но во время теста его скорость и направление сильно не изменились. (Я надеялся, что в 6 утра вообще будет тишина).
Итак, давайте смотреть результаты. Я все данные внес в электронную таблицу и сделал графики.
Скорость 50 км/ч на расстояние 50 км (29 км в одну сторону и 21 км в обратную).
Итак, на скорости 50 км/ч автомобиль крутил двигатель на уровне 1100 оборотов в минуту. Итоговый расход топлива после 50-километрового участка составил 5,5 л/100 км.
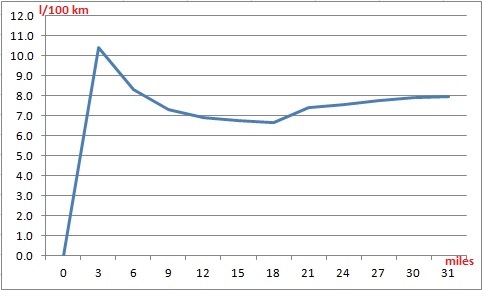
Теперь туже дорогу, но уже на скорости 100 км/ч:
Так же видно из графиков, что кривые очень схожи. Единственное, разный уровень расхода топлива на скоростях 50 км/ч и 100 км/ч. Так на более высокой скорости средний расход топлива за весь участок длиной 50 км составил 7,9 л/100 км. В этом тесте тахометр показывал примерно 2000 оборотов в минуту.
Другими словами, с ростом скорости возрастает и расход топлива, в том числе и из-за многократно выросшего лобового аэродинамического сопротивления (при увеличении скорости, аэродинамическое сопротивление возрастает пропорционально квадрату [подправил для особо придирчивых]).
Задачи на движение

— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов. Получить карточки с задачами разных видов можно по ссылке.
Время, скорость, расстояние
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 м
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 м
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.