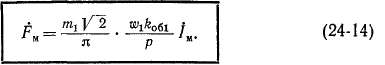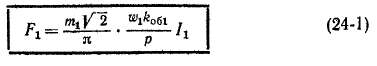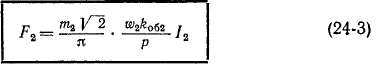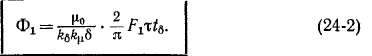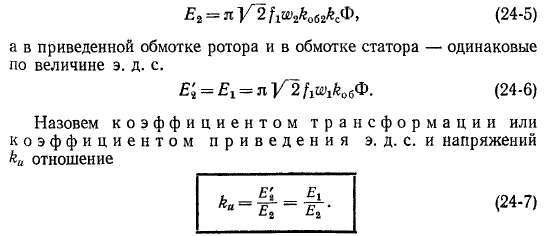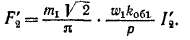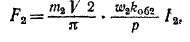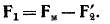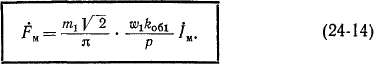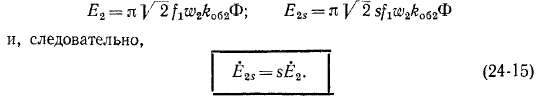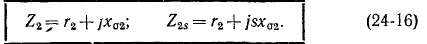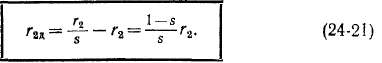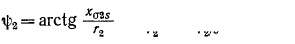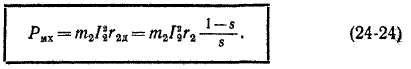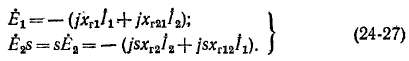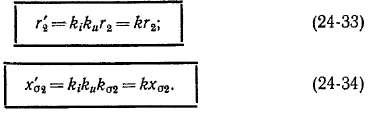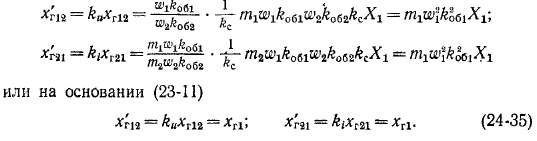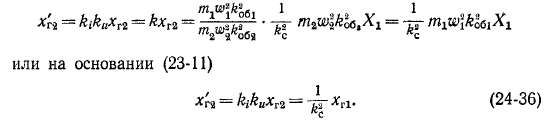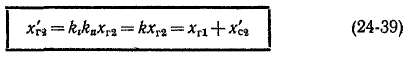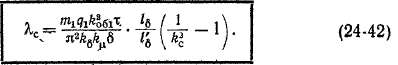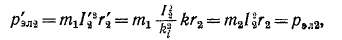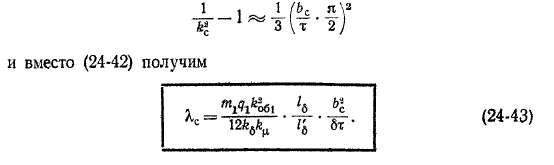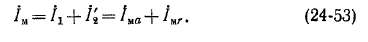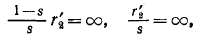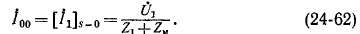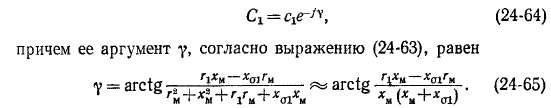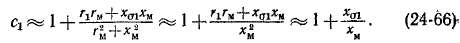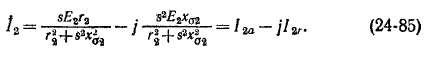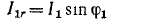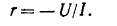Приведение обмотки ротора асинхронной машины к статорной

Содержание

Приведение обмотки ротора к обмотке статора.

В тех же целях, как и для трансформатора, приведем вторичную обмотку асинхронной машины к первичной. Для этого можно представить себе, что реальная вторичная обмотка заменяется приведенной, которая устроена так же, как и первичная обмотка, и имеет с нею одинаковые числа фаз и витков в фазе, а также одинаковый обмоточный коэффициент основной гармоники.

Приведенные величины будем обозначать штрихами. Приведенные напряжения и токи вторичной обмотки должны быть рассчитаны так, чтобы энергетические и основные электромагнитные соотношения в машине не нарушались.

В общем случае надо иметь в виду, что пазы ротора и статора асинхронной машины могут быть скошены относительно друг друга. Обычно в асинхронных машинах скошены пазы ротора, а пазы статора являются прямыми. Поэтому при приведении обмотки ротора к обмотке статора необходимо представить себе, что приведенная обмотка ротора также имеет прямые пазы. Таким образом, в приведенной машине основные гармоники полей статора и ротора и их результирующего поля будут ориентированы вдоль прямых пазов, в осевом направлении, т. е. эти поля не будут скошены в тангенциальном направлении. Поэтому соотношения между неприведен-ными и приведенными величи-нами целесообразно установить, исходя из нескошенного магнитного поля. Для ясности положим, что выражения для обмоточных коэффициентов статора k_o61 и ротора k_o62 содержат в качестве сомножителей только коэффициенты укорочения и распределения обмотки, а влияние скоса будем учитывать с помощью коэффициента скоса k_c [см. равенство (20-3)], вводимого в качестве дополнительного множителя.

Нескошенное магнитное поле основной гармоники с потоком величиной Ф индуктирует в обмотке неподвижного ротора со скошенными пазами э. д. с.

Согласно выражениям (24-5) и (24-6),

Приведенная обмотка ротора с приведенным током /£ создает основную гармонику н. с, которая ориентирована в осевом направлении и имеет амплитуду

Неприведенная обмотка ротора создает основную гармонику н. с, которая ориентирована вдоль скошенных пазов ротора и имеет амплитуду

Это выражение не содержит коэффициента k_c. Однако при вычис-лещпмютокосцепления взаимной индукции с обмоткой статора, соз* даваемого н. с. F_tt надо учитывать коэффициент скоса k_c, так как, н. с. f_g и создаваемый ею поток скошены относительно обмотки статора. Поэтому в отношении статора эффективной является н. с. kj и при приведении должно быть соблюдено равенство

Коэффициенты трансформавди \ и к, при т_х ^ щ не равны, Э»ак как при данном токе / намагничивающее действие и н. с. обмотки зависит от числа фаз т и нря яр«ведед»и вторичная обмотка с числом фаз щ заменяется обмоткой с числом фаз т*. В otличйe от транс*

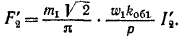
форматора для асинхронной машины в выражения для k,, и k_l входят также обмоточные коэффициенты.

При отсутствии взаимного скоса пазов в равенствах (24-8) и (24-10) необходимо положить k_z = 1.

Обычно скос пазов относительно невелик и коэффициент k_c близок к единице. Если, например, скос пазов ротора Ь_с равен зубцовому делению статора, то при количествах пазов статора на полюс ZJ2p = 3 и 6 соответственно имеем bjx = 1 /₃ и V₆. При этом, согласно выражению (20-3), получим соответственно k_c =

Рис 24-2 Пространственная (а) и временная (б) векторные

диаграммы асинхронной машины с заторможенным ротором

при совпадении осей фаз статора и ротора

= 0,955 и 0,989. Тем не менее и при относительно небольшом скосе, как будет показано ниже, заметным образом возрастает электромагнитное рассеяние машины.

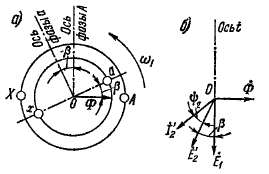
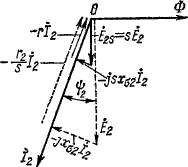
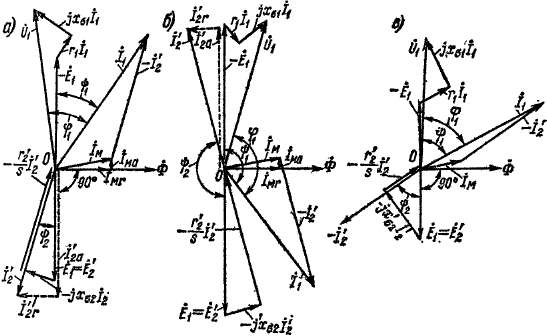
Пространственные и временные векторные диаграммы.Рассмотрим пространственные и временные фазовые соотношения (сдвиги по фазе) первичных и вторичных электромагнитных величин и допустим сначала, что оси фаз обмоток статора и ротора совпадают (рис. 24-2). При этом, не нарушая общности выводов, будем иметь в виду для простоты двухполюсную машину с трехфазными обмотками на статоре и роторе и построим пространственную (рис. 24-2, а) и временную (рис. 24-2, б) векторные диаграммы токов, намагничивающих сил и потоков. На временной векторной диаграмме будем откладывать векторы э. д. с. и токов фаз Лий.

Положительная пространственная ось фаз Л и а обмоток статора и ротора на рис. 24-2, а и ось времени диаграммы рис. 24-2, б направлены вверх. Токи в фазах Л и а положительны, когда они создают потоки в направлении положительных осей этих фаз, т. е. когда

Диаграмма рис. 24-2, а построена для момента времени, когда потокосцепления фаз А и а от результирующего потока Ф равны нулю и достигают положительных максимумов через четверть периода тока. При этом пространственный вектор потока Ф на рис. 24-2, а и временной вектор этого же потока Ф на рис. 24-2, б будут направо лены одинаково, а именно вправо.

Э, д. с. £_х и Ёъ или э. д. с. Ei и £а, индуктируемые в фазах А: и а результирующим потоком Ф, вследствие совпадения осей этих фаз обмоток совпадают ио фазе во времени (рис. 24-2, б). В рассмат-: риваемый момент времени они проходят через отрицательный максимум, как это следует из рис. 24-2, б и как это можно также установить-из рис. 24-2, а по правилу правой руки.

Если нагрузочное сопротивление Z_Hf (см. рис. 24-1) имеет активную и индуктивную составляющие, то ток /g отстает от э. д. с. j§a на некоторый угол ij)₂ (рис. 24-2, б). Временной вектор н. с. вторичной обмотки £^ = k_cB% и временной вектор потока вторичной обмотки Ф£ = £_сФ_а совпадают по фазе с вектором тока (рис. 24-2, б). Согласно рис. 24-2, б, ток /£ достигнет своего отрицательного максимума через отрезок.времени, соответствующий’углу; •ф₂. В момент достижения током фазы а отрицательного максимума пространственный вектор н. с. Fg на рис. 24-2, а будет направлен вертикально вниз. Так как векторы на рис. 24-2, an б совершают один оборот в течение одного периода тока и поэтому в течение одинаковых отрезков времени поворачиваются на одинаковые углы, то вектор Fa на рис. 24-2, аъ рассматриваемый момент времени также будет сдвинут от отрицательного направления вертикали в сторону отставания на угол гр₂„

Пространственный вектор основной гармоники результирующей н. с. обмоток статора и ротора

представляет собой геометрическую сумму их н. с. и будет совпадать на рис. 24-2, а с направлением вектора Ф. Исходя из соотношения (24-11), на рис. 24-2, а можно построить также пространственный вектор н. с. первичной обмотки:

Пространственный вектор потока первичной обмотки Ф_х совпадает в пространстве по фазе с вектором F_t (рис. 24-2, а), и для векторов потока существует соотношение

аналогичное соотношению для пространственных векторов соответствующих н. с.

Параллельно векторам н. с. F_t и F£ на рис. 24-2, а можно построить также пространственные векторы пропорциональных им токов первичной и вторичной обмоток Ii и Y% Эти последние векторы можно рассматривать и как пространственные векторы вращающихся пространственных волн тока или линейной нагрузки первичной и вторичной обмоток (см. § 22-4). Однако при этом необходимо иметь в виду, что в действительности указанные волны тока сдвинуты в пространстве от волн соответствующих н. с. на 90°. Поэтому совмещение направлений этих векторов на рис. 24-2, а соответствует повороту векторов волн тока яа 90° и является в этом смысле условным.

На основании выражений (24-1Х,(24-3) и (24-11) результирующая н. с.

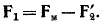
как и у трансформаторов, называют намагничивающим током. Согласно выражениям (24-12) и (24-13),

Исходя из соотношения (24-13), на рис. 24-2, а можно изобразить также пространственный вектор намагничивающего тока 1_М, совпадающий по направлению с вектором результирующего потока Ф. Соотношение (24-13) действительно также для временных векторов 1_и 1’ч и /_м (рис. 24-2, б). На рис. 24-2, б можно построить также временные векторы потоков и н. с. первичной (Ф_ь Д) и вторичной (Ф^, Fj) обмоток, совпадающие по фазе с токами /_х и /д, и их результирующие векторы Ф и F,,

Таким образом, пространственные и временные векторы диаграммы электромагнитных величин асинхронной машины с заторможенным ротором при совпадении осей фаз обмоток статора и ротора совершенно идентичны. В частности, волны н. с. обмоток статора и ротора сдвинуты в пространстве вдоль окружности машины на такие же углы, на какие сдвинуты по фазе токи соответствующих фаз этих обмоток, и т. д.

Очевидно, что все изложенное справедливо и для многофазных машин с любыми, в том числе и неравными, числами фаз статора и ротора и при любом числе пар полюсов машины р. При этом ввиду идентичности электромагнитных величин на протяжении различных пар полюсов можно рассматривать лишь одну пару полюсов или двухполюсную машину. В этом случае углы на рис. 24-2, а являются электрическими, которые больше действительных, геометрических углов В машине в р раз.

Вместо векторов потоков на рис. 24-2, а можно изображать также пропорциональные им и одинаково направленные векторы потоко-сцеплений W этих потоков с фазами обмоток.

Нетрудно также установить, что проекции векторов токов и по-токосцеплений на оси фаз Aw. а (рис. 24-2, а), а также на оси других фаз определяют мгновенные значения токов и потокосцепле-ний соответствующих фаз. Отметим также, что развитые в связи с рассмотрением рис. 24-2, а представления о пространственных векторах широко используются в современной математической теории переходных процессов машин переменного тока.

Систематическое изложение основ этой теории, однако, не укладывается в рамки данной книги.

Диаграмма временных векторов Ф, F, / и Ё (рис. 24-2, б) вполне аналогична соответствующей части векторной диаграммы трансформаторов без учета магнитных потерь. Диаграмму рис. 24-2, б можно дополнить, построив: 1) векторы падений напряжения в активных сопротивлениях (г_ъ г’%) и индуктивных сопротивлениях рассеяния (x_ai, х_о‘ъ) обмоток и 2) векторы напряжений обмоток. Получаемая при этом диаграмма также вполне аналогична диаграмме трансформатора.

Векторы напряжений й_у и (У’₂ и э. д. с. Ё_х и Ё\ также можно перенести на диаграмму рис. 24-2, а, придав им смысл пространственных вращающихся векторов напряжений и э. д. с. Проекции этих векторов на оси фаз обмоток также будут определять мгновенные значения напряжений и э. д. с. соответствующих фаз обмоток.

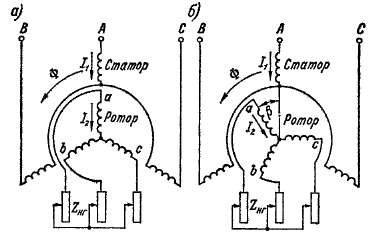
Случай несовпадения осей фаз обмоток статора и ротора.Предположим для определенности, что ось фазы а ротора сдвинута относительно оси фазы А статора на электрический угол Р в сторону вращения поля (рис. 24-1,6 и 24-3, а). При этом токи обмоток статора и ротора также создают общее вращающееся магнитное поле, однако результирующий вращающийся поток Ф будет набегать на фазу А раньше, чем на фазу а, и поэтому э. д. с. ротора Ё\ будет отставать во времени от э. д. с. статора Ё_г на угол р(рис. 24-3, б). Если сопротивление нагрузки Z_Hr остается неизменным, то ток Г_г будет отставать от э. д. с. Ё’% на такой же угол а|э₂, как и на рис. 24-2, б, однако по сравнению со схемой рис. 24-2 ток \’_% также будет отставать во времени на угол р. Поэтому на рис. 24-3, а пространственная сину’ соидальная волна или вектор вращающейся вторичной н. с. F£ достигнет оси фазы а и совпадет сней по направлению на некоторый отрезок времени позднее, чем на рис. 24-2, а. Величина этого отрезка времени соответствует повороту вектора F’_% на угол р. Поскольку, однако, на рис. 24-3 ось фазы а сдвинута на угол рвперед, то отсюда следует, что вектор F£ и в этом случае займет по отношению к вектору Ф и другим векторам такое же положение, как и на рис. 24-2, а. Иными словами, перемещение обмотки ротора на угол рв сторону вращения поля вызывает отставание векторов тока 1^ и н. с. F^

Рис. 24-3. Определение характера пространственных и временных векторных диаграмм асинхронной машины с заторможенным ротором при несовпадении осей фаз статора и ротора

относительно оси этой обмотки на угол ($, но вследствие смещения обмотки ротора на такой же угол вперед положение этой н. с. относительно статора и его н. с. не изменится. Поэтому останутся неизменными также результирующая н. с. F_M и результирующий поток. Не изменится также режим работы машины в целом и вели* ^шны всех токов, напряжений и мощности, за исключением вторичных tqkob, э. д. с. и напряжений, которые изменятся по фазе* Пространственная векторная диаграмма рис. 24-2, а также останется неизменной. При этом нетрудно установить, что проекции векторов рис. 24-2, а на оси фаз будут правильно определять истинные мгновенные значения токов и потокосцеплении фаз статора и ротора при. любом положении ротора.

Таким образом, режим работы заторможенной асинхронно^ машины не зависит от положения ротора, если не учитывать незна* чительного влияния, вызываемого изменением взаимного положения зубцов статора и ротора при изменении положения послед» него.

При любом положении ротора полностью действительны также пространственная векторная диаграмма рис. 24-2, а и временная векторная диаграмма рис. 24-2, б. При использовании временной диаграммы рис. 24-2, б надо только иметь в виду, что при р» ^ь О реальные вторичные токи и «апряжения сдвинуты по сравнению с их положением нарис. 24-2, б на угол р\ и в общем случае представленное на рис. 24-2, б сложение векторов 1_г и Г% необходимо истолковывать в смысле геометрического сложения вращающихся волн н. a Fj и F^ соответственно рис, 24-2, а.

§24-2. Приведение рабочего* процессу асинхронной машины при вращающемся роторе к рабочему процессу при неподвижном роторе

Общие положения.При неподвижном роторе, как было установлено в § 24-1, асинхронная машина работает как трансформатор., в котором электрическая энергия первичной цепи за вычетом потерь превращается в электрическую же энергию вторичной цепи. Во вращающейся же асинхронной машине в двигательном режиме, работы электрическая энергия, потребляемая первичной обмоткой из питающей сети, за вычетом потерь в машине превращается в механическую энергию на валу машины. В генераторном режиме, наоборот-, механическая энергия, подводимая к валу, превращается в электриче-сжую энергию в первичной обмотке и передается в сеть. Кроме того, режим работы асинхронной машины при вращающемся роторе более сложен в том отношении, что в этом случае частоты токов первичной и вторичной цепей не равны (см. § 19-2), По этой причине, в част-

ности, невозможно изображение первичных и вторичных электрических величин на общих временных векторных диаграммах.

Вследствие изложенного, естественно, возникает мысль о замене вращающейся асинхронной машины эквивалентной ей по энергетическим И электромагнитным соотношениям машиной с заторможенным ротором или, иначе говоря, о приведении режима работы вращающейся асинхронной машины к эквивалентному режиму работы этой же машины при неподвижном роторе.

остаются, естественно, неизменными.

Векторные диаграммы вторичной цепи асинхронного двигателя при вращающемся роторе и в эквивалентном режиме с неподвижным ротором изображены на рис. 24-4. Следует иметь в виду, что в рассматриваемых двух режимах частоты тока /₂ различны.

Равенства (24-17) и (24-18) показывают, что при переходе машины в режим работы с неподвижным ротором э. д. с. и индуктивное сопротивление вторичной цепи будут соответствовать реальным значениям этих величин при неподвижном роторе, но вместо активного сопротивления г₂ эта цепь должна содержать сопротивление rjs, т. е. активное сопротивление должно быть увеличено на величину

Источник

Приведение параметров обмотки ротора и векторная диаграмма асинхронного двигателя

Чтобы векторы ЭДС, напряжений и токов обмоток статора и ротора можно было изобразить на одной векторной диаграмме, следует параметры обмотки ротора привести к обмотке статора, т. е. обмотку ротора с числом фаз m₂, обмоточным коэффициентом k_o₆₂ и числом витков одной фазной обмоткиω₂ заменить обмоткой с m₁, ω₁ и k_об1. При этом мощности и фазовые сдвиги векторов ЭДС и токов ротора после приведения должны остаться такими же, что и до приведения. Пересчет реальных параметров обмотки ротора на приведенные выполняется по формулам, аналогичным формулам приведения параметров вторичной обмотки трансформатора (см. § 1.6).

При s = 1 приведенная ЭДС ротора

В отличие от трансформаторов в асинхронных двигателях коэффициенты трансформации напряжения и тока не равны ( k_е ≠ k_i ). Объясняется это тем, что число фаз в обмотках статора и ротора в общем случае не одинаково ( m₁ ≠ m₂ ). Лишь в двигателях с фазным ротором, у которых m₁ = m₂, эти коэффициенты равны.

Активное и индуктивное приведенные сопротивления обмотки ротора:

Величину r′₂/ s можно представить в виде

= — + r ′ ₂ = r ′ ₂ + r ′ ₂ (12.21)

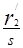
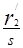
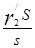
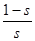
тогда уравнение ЭДС для цепи ротора в приведенных параметрах примет вид

Для асинхронного двигателя (так же как и для трансформатора) можно построить векторную диаграмму. Основанием для построения этой диаграммы являются уравнение токов (12.14) и уравнения напряжений обмоток статора (12.3) и ротора

Угол сдвига фаз между ЭДС 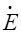′ ₂ и током ′ ₂

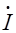
Так как векторную диаграмму асинхронного двигателя строят по уравнениям напряжений и токов, аналогичным уравнениям трансформатора, то порядок построения этой диаграммы такой же, что и векторной диаграммы трансформатора (см. § 1.7).

Рис. 12.1 Векторная диаграмма

На рис. 12.1 представлена векторная диаграмма асинхронного двигателя. От векторной диаграммы трансформатора (см. рис. 1.19) она отличается тем, что сумма падений напряжения в обмотке ротора (во вторичной обмотке) уравновешивается ЭДС 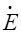′ ₂ обмотки неподвижного ротора (n₂ = 0), так как обмотка ротора замкнутой накоротко. Однако если падение напряжения = ′ ₂r ′ ₂ (1-s)/ sрассматривать как напряжение на некоторой активной нагрузке r ′ ₂ (1-s)/ s, подключенной на зажимы неподвижного ротора, то векторную диаграмму асинхронного двигателя можно рассматривать как векторную диаграмму трансформатора, на зажимы вторичной обмотки которого подключено переменное активное сопротивление r₂ (1-s)/ s. Иначе говоря, асинхронный двигатель в электрическом отношении подобен трансформатору работающему на чисто активную нагрузку. Активная мощность вторичной обмотки такого трансформатора

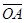
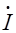
представляет собой полную механическую мощность, развиваемую асинхронным двигателем.

Уравнениям напряжений и токов, а также векторной диаграмме асинхронного двигателя соответствует электрическая схема замещения асинхронного двигателя.

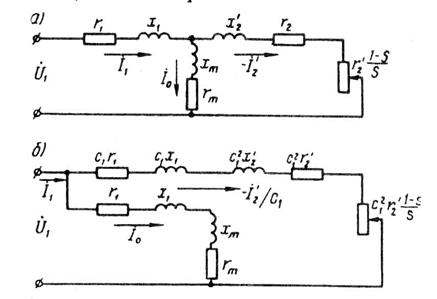
Рис. 12.2. Схемы замещения асинхронного

Воспользовавшись Г-образной схемой замещения и приняв с₁ = 1, запишем выражение тока в рабочем контуре:

I ′ ₂ = 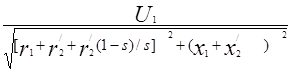(12.24)

или с учетом (12.21) получим

1. В чем сходство и в чем различие между асинхронным двигателем и трансформатором?

2. Почему с увеличением механической нагрузки на вал асинхронного двигателя возрастает потребляемая из сети двигателем мощность?

3. Каков порядок построения векторной диаграммы двигателя?

4. В чем отличие Г-образной схемы замещения от Т-образной?

ГЛАВА 13

• Электромагнитный момент и рабочие характеристики асинхронного двигателя

Источник

Приведение обмотки ротора асинхронной машины к статорной

Основы теории. Вращающие моменты и механические характеристики. Круговая диаграмма. Двигатели с вытеснением тока в обмотке ротора. Пуск и регулирование скорости вращения. Особые виды и режимы работы многофазных машин. Однофазные машины. Микромашины автоматических устройств.

Глава двадцать четвертая ОСНОВЫ ТЕОРИИ АСИНХРОННЫХ МАШИН

§ 24-1. Асинхронная машина при неподвижном роторе

Общая характеристика режима работы. Ниже будем иметь в виду симметричную Многофазную асинхронную машину и симметричные режимы ее работы, когда сопротивления фаз каждой обмотки одинаковы, а напряжения и токи каждой обмотки- составляют симметричныесистемы прямой последовательности. Кроме того, предположим, что взаимная индукция между статором и ротором обусловливается только основной гармоникой магнитного поля в воздушном зазоре, а высшие гармоники этого подя относятся к рассеянию и учитываются в индуктивных сопротивлениях рассеяния. При этом можно представить себе, что в воздушном зазоре действуют только основные гармоники поля обеих обмоток. Будем также предполагать, что обмотка статора является первичной и подключается к сети, а обмотка ротора — вторичной.

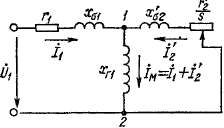
Рассмотрим многофазную асинхронную машийу с заторможенным ротором. Для определенности будем иметь в виду машину с трехфазными обмотками на статоре и роторе (рис. 24-1). Предположим, что первичная обмотка включается в трехфазную сеть с фазным напряжением U_it а к фазам вторичной обмотки подключаются сопротивления нагрузки Z_sx.

При указанных условиях асинхронная машина работает как трансформатор. Симметричные первичные фазные токи 1_Х создают основную гармонику н. с. с амплитудой на полюс

и первичный вращающийся магнитный поток на один полюс

Индуктируемые во вторичной обмотке токи /₂ создают основную гармонику н. с. с амплитудой

и вторичный вращающийся магнитный поток на полюс

Рис. 24-1. Схемы асинхронной машины с заторможенным ротором при совпадении (а) и несовпадении (б) осей фаз обмоток статора и ротора

ности в действительности не существуют, и магнитное состояние машины и степень насыщения магнитной цепи определяются величиной результирующего потока Ф.

Как и у трансформатора, результирующий поток индуктирует в первичной и вторичной обмотках э. д. с. Е_г и Е₂, величины которых определяются равенством (20-19). Величина напряжения на сопротивлении нагрузки U₂ равна Е_% минус падение напряжения во вторичной обмотке.

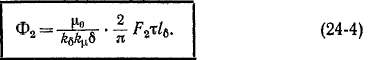
Приведение обмотки ротора к обмотке статора.

Согласно выражениям (24-5) и (24-6),

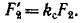
форматора для асинхронной машины в выражения для k,, и k_l входят также обмоточные коэффициенты.

При отсутствии взаимного скоса пазов в равенствах (24-8) и (24-10) необходимо положить k_z = 1.

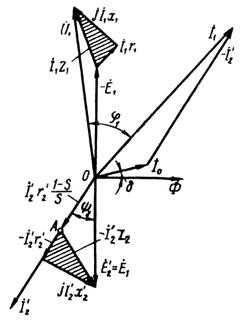
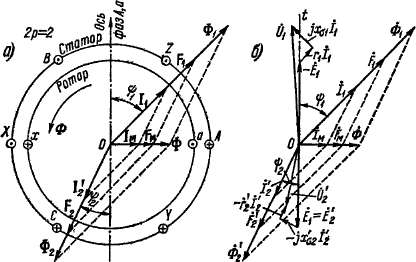
Рис 24-2 Пространственная (а) и временная (б) векторные

диаграммы асинхронной машины с заторможенным ротором

при совпадении осей фаз статора и ротора

Пространственные и временные векторные диаграммы. Рассмот рим пространственные и временные фазовые соотношения (сдвиги по фазе) первичных и вторичных электромагнитных величин и допустим сначала, что оси фаз обмоток статора и ротора совпадают (рис. 24-2). При этом, не нарушая общности выводов, будем иметь в виду для простоты двухполюсную машину с трехфазными обмотками на статоре и роторе и построим пространственную (рис. 24-2, а) и временную (рис. 24-2, б) векторные диаграммы токов, намагничивающих сил и потоков. На временной векторной диаграмме будем откладывать векторы э. д. с. и токов фаз Лий.

Пространственный вектор основной гармоники результирующей н. с. обмоток статора и ротора

аналогичное соотношению для пространственных векторов соответствующих н. с.

На основании выражений (24-1Х, (24-3) и (24-11) результирующая н. с.

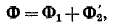
как и у трансформаторов, называют намагничивающим током. Согласно выражениям (24-12) и (24-13),

Систематическое изложение основ этой теории, однако, не укладывается в рамки данной книги.

Случай несовпадения осей фаз обмоток статора и ротора. Пред положим для определенности, что ось фазы а ротора сдвинута относительно оси фазы А статора на электрический угол Р в сторону вращения поля (рис. 24-1,6 и 24-3, а). При этом токи обмоток статора и ротора также создают общее вращающееся магнитное поле, однако результирующий вращающийся поток Ф будет набегать на фазу А раньше, чем на фазу а, и поэтому э. д. с. ротора Ё\ будет отставать во времени от э. д. с. статора Ё_г на угол р (рис. 24-3, б). Если сопротивление нагрузки Z_Hr остается неизменным, то ток Г_г будет отставать от э. д. с. Ё’% на такой же угол а|э₂, как и на рис. 24-2, б, однако по сравнению со схемой рис. 24-2 ток \’_% также будет отставать во времени на угол р. Поэтому на рис. 24-3, а пространственная сину’ соидальная волна или вектор вращающейся вторичной н. с. F£ достигнет оси фазы а и совпадет с ней по направлению на некоторый отрезок времени позднее, чем на рис. 24-2, а. Величина этого отрезка времени соответствует повороту вектора F’_% на угол р. Поскольку, однако, на рис. 24-3 ось фазы а сдвинута на угол р вперед, то отсюда следует, что вектор F£ и в этом случае займет по отношению к вектору Ф и другим векторам такое же положение, как и на рис. 24-2, а. Иными словами, перемещение обмотки ротора на угол р в сторону вращения поля вызывает отставание векторов тока 1^ и н. с. F^

§ 24-2. Приведение рабочего* процессу асинхронной машины при вращающемся роторе к рабочему процессу при неподвижном роторе

Общие положения. При неподвижном роторе, как было установлено в § 24-1, асинхронная машина работает как трансформатор., в котором электрическая энергия первичной цепи за вычетом потерь превращается в электрическую же энергию вторичной цепи. Во вращающейся же асинхронной машине в двигательном режиме, работы электрическая энергия, потребляемая первичной обмоткой из питающей сети, за вычетом потерь в машине превращается в механическую энергию на валу машины. В генераторном режиме, наоборот-, механическая энергия, подводимая к валу, превращается в электриче-сжую энергию в первичной обмотке и передается в сеть. Кроме того, режим работы асинхронной машины при вращающемся роторе более сложен в том отношении, что в этом случае частоты токов первичной и вторичной цепей не равны (см. § 19-2), По этой причине, в част-

Такое приведение оказывается возможным потому, что и при вращающемся роторе н. с. и магнитные поля обмотки статора и ротора вращаются синхронно и образуют общее вращающееся поле (см. § 19-2), точнее, потому, что

В связи с изложенным можно заключить, что при приведении режима работы ^вращающейся машины к эквивалентному режиму неподвижной машины необходимо, чтобы ее пространственная векторная диаграмма не изменилась, т. е. чтобы сохранились величины токов ив. с обмоток и их фазные сдвиги относительно друг друга. При этих условиях остаются неизменными величины результирующих н. с. и магнитных потоков, энергия магнитных полей, потребляемой из сети первичной мощности, магнитных и электрических потерь в статоре, передаваемой через магнитное поле со статора на ротор электромагнитной мощности и т. д. Единственным существенным отличием неподвижной машины будет то, что в ней не происходит преобразования механической энергии в электрическую и гэбратно. Поэтому при переходе к неподвижной машине механическая мощность должна быть представлена равной ей электрической мощностью.

Количественные соотношения. Величину э. д. с, индуктируемой результирующим магнитным потоком Ф в фазе вторичной

обмотки при неподвижном роторе, когда s == 1 и /₂ = /_ь будем по-прежнему обозначать буквой Е₂, а величину этой э. д. с. при той же величине потока Ф, но при любом скольжении s, когда /₂ = sf_ly обозначим £_2S. При этом

Здесь х_а% — индуктивное сопротивление рассеяния вторичной цепи при неподвижном роторе или при /_а = f_lt a x_ais — величина этого сопротивления при любом скольжении.

Величины полного сопротивления вторичной цепи при неподвижном и вращающемся роторе соответственно будут

Если к вторичной обмотке подключено некоторое внешнее сопротивление, то г₃ и х_а2 должны включать в себя также составляющие этого сопротивления.

Согласно выражениям (24-15) и (24-16), величина вторичного тока /₂ при вращающемся с любым скольжением роторе

Разделим числитель и знаменатель правой части (24-17) на s. Тогда

Левая часть равенств (24-17) и (24-18) представляет собой комплекс вторичного тока при вращающемся роторе, который при переходе машины к эквивалентному режиму с неподвижным ротором

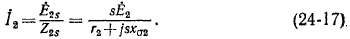
остается неизменным. В числителе правой части выражения (24-18) стоит величина вторичной э. д. с. при неподвижном роторе. Поэтому знаменатель правой части (24-18) указывает на то, что при переходе машины к режиму с неподвижным ротором для сохранения величины и фазы вторичного тока неизменными вторичная цепь должна обладать сопротивлением

Если, например, s = 0,05, то 1/s = 20 и сравнение равенств (24-17) и (24-18) показывает, что при переходе машины к режиму с неподвижным ротором э. д. с. вторичной цепи увеличивается в 20 раз и одновременно во столько же раз должны быть увеличены обе составляющие вторичного сопротивления. При этих условиях как величина тока /₂, так и величина его фазного угла сдвига

остаются, естественно, неизменными.

В двигательном режиме (0

Рис. 24-4. Векторная диаграмма вторичной цепи асинхронного двигателя при вращающемся (сплошные веьто-ры) и неподвижном (штриховые векторы) роторе

Величина электромагнитной мощности Р_8м, передаваемой посреди ством магнитного поля со статора на ротор, в обоих рассматриваемых режимах одинакова. Одинаковы также электрические потери во вторичной обмотке машины:

Разность мощностей Р_9м и р_ЭЛ2-в обоих режимах тоже одинакова. В реальном рабочем режиме с вращающимся ротором разность этих мощностей превращается в механическую мощность на роторе

В эквивалентном режиме механическая мощность равна нулю; так как ротор неподвижен, но при этом развивается электрическая мощность в добавочном сопротивлении г_гл. Очевидно, что эта щощ* ность должна быть равна механической мощности в режиме с вращающимся ротором:

Таким образом, мощность, выделяемая в трех фазах в сопротивлениях г_2д, равна механической мощности вращающейся машины.

В рассматриваемых выше выражениях были использованы не* приведенные значения вторичных величин. Вместо них, как будет выяснено ниже, можно пользоваться также приведенными величинами.

§ 24-3. Уравнения напряжений асинхронной машины и их преобразование

Уравнения напряжений неприведенной асинхронной машины.

Составим уравнения напряжения для одной фазы первичной обмотки и одной фазы вторичной обмотки асинхронной машины с вращающимся ротором. В соответствии с изложенным в § 24-1 и 24-2 эти уравнения можно написать для такого момента времени или положения ротора, когда оси рассматриваемых фаз двух обмоток совпадают. Предположим, что вторичная цепь замкнута накоротко и поэтому ее напряжение равно нулю. Допустим также, что магнитные потери в сердечниках статора и ротора равны нулю. Сначала напишем уравнения для неприведенной вторичной обмотки.

При перечисленных предположениях уравнения напряжения можно написать в следующей форме:

Здесь и_г — первичное фазное напряжение; 1_Х и /₂ — первичный и вторичный фазные токи: г_х, г₂ — первичное и вторичное активные сопротивления; x_n, x_a2 — первичное и вторичное индуктивные» сопротивления рассеяния, включающие пазовое, лобовое, дифференциальное рассеяния и рассеяние по коронкам зубцов (см. § 23-3): х_т1, х_п — первичное и вторичное главные собственные индуктивные сопротивления, учитывающие основные гармоники магнитного поля в воздушном зазоре (см. § 23-2); х_п1, х_пг — взаимные индуктивные сопротивления первичной и вторичной обмоток от основных гармоник поля в воздушном зазоре, причем в общем случае х_тП ф х_пг (см. § 23-2).

Все перечисленные сопротивления х соответствуют первичной частоте. Множители s в уравнении (24-26) учитывают то обстоятельство, что при вращающемся роторе вторичные частота,- э. д. с. и индуктивные сопротивления пропорциональны скольжению s. Э. д, с, взаимной индукции во вторичной обмотке

индуктированная первичным током и соответствующая последнему члену (24-26), также пропорциональна s, поскольку скорость вращения первичного поля относительно вторичной обмотки также пропорциональна скольжению.

Суммы носледних двух членов (24-25) и (24-26), взятые с обратным знаком, представляют собой э. д. с, индуктированные в первичной и вторичной обмотках результирующим магнитным потоком основных гармоник полей статора и ротора:

Преобразование уравнений напряжений и приведенные пара метры машины. Разделим, во-первых, все члены уравнения (24-26) на s, что, согласно изложенному в § 24-2, соответствует переходу

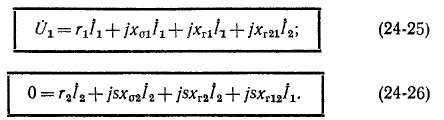
к машине с заторможенным ротором. Во-вторых, перейдем к приведенным вторичным величинам, для чего в соответствии с соотношением (24-9) сделаем в (24-25) и (24-26) подстановку

и умножим также уравнение (24-26) на k_u [см. равенство (24-8)1. Последняя операция, согласно выражению (24-7), соответствует приведению падений напряжения и э. д. с. реальной вторичной обмотки, представленных членами уравнения (24-26), к значениям этих величин для приведенной обмотки. В результате вместо (24-25) и (24-26) получим

коэффициентом приведения сопротивлений вторичной цепи к первичной. На основании выражений (24-8) и (24-10)

В равенство (24-30) можно ввести приведенные значения вторичных активного сопротивления и индуктивного сопротивления рассеяния:

Другие члены (24-29) и (24-30) преобразовываются следующим образом.

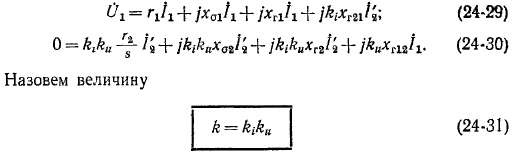
Приведенные величины индуктивных сопротивлений взаимной индукции, согласно выражениям (23-17), (23-18), (24-8) и (24-10),

Таким образом, приведенные взаимные индуктивные сопротивления оказываются равными главному индуктивному сопрб-тивлению первичной обмотки, обусловленному основной гармоникой поля этой обмотки.

Этот результат вполне естествен, так как после приведения первичная и вторичная обмотки становятся одинаковыми и поэтому их главные собственные и взаимные индуктивные сопротивления должны быть равны.

Далее, для третьего члена правой части (24-30) на основании выражений (23-14), (24-8) и (24-10) получим

Определение индуктивного сопротивления рассеяния скоса. При

отсутствии скоса (k_c = 1), согласно выражению (24-36), х/_% = х_гЪ т. е. главные индуктивные сопротивления первичной и приведенной вторичной обмоток равны, что также является естественным.

Однако при наличии скоса (k_c ^ 1) будет Хг₂ > х_1г, что указывает на то, что в этом случае возникает дополнительное электромагнитное рассеяние за счет основной гармоники поля вторичной обмотки. Физически это обусловлено тем, что при наличии скоса пазов э. д. с. взаимной индукции уменьшается.

Приведенное значение индуктивного сопротивления рассеяния вторичной обмотки от скоса пазов, таким образом, равно

Несмотря на то что k_c может мало отличаться от единицы, значение Хс₂ по сравнению с другими составляющими индуктивного сопротивления рассеяния достаточно велико, так как х_г1 является большой величиной. Если, например, k_c = 0,99 и х_гЫ — 4,0, то *с2* — 0.0813, что составляет весьма значительную величину..

Согласно (24-37), приведенное значение вторичного главного сопротивления

представляется в виде суммы главного индуктивного сопротивления приведенной вторичной обмотки и индуктивного сопротивления рассеяния скоса.

В выражении (24-40) сопротивление рассеяния Ха₂ включает в себя все составлдющие сопротивления рассеяния вторичной обмотки, в том числе сопротивление рассеяния скоса.

Последние члены уравнений (24-40), взятые

Нетрудно установить, что в результате приведения вторичной обмотки к первичной все энергетические соотношения сохраняются.

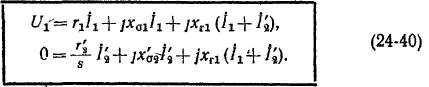
Например, согласно выражениям (24-28), (24-33), (24-32) и (24-10), электрические потери в приведенной вторичной обмотке

равны потерям в действительной вторичной обмотке.

Отметим также, что приведение вторичной обмотки к первичной можно в принципе выполнять также с коэффициентами k_a и k_h отличающимися от соотношений (24-8) и (24-10),

В частности, эти коэффициенты можно выбрать такими, что индуктивное сопротивление рассеяния скоса будет фигурировать в качестве составляющего, индуктивного сопротивления рассеяния первичной цепи, а не вторичной. Можно также распределить сопротивление рассеяния скоса между обеими цепями. Однако подобный подход нерационален, так как это без надобности усложняет расчеты. К тому же скос в асинхронных машинах обычно выполняется на роторе, т. е. на вторичной стороне машины. Поэтому и с физической точки зрения это сопротивление рассеяния целесообразно отнести к вторичной цепи.

О расчете индуктивного сопротивления рассеяния скоса. Относительную магнитную рроводимость рассеяния скоса к_с, входящую в (23-45), можно определить по формуле (23-42), заменив там к_х на %_z и х_д на *с2 из (24-38) и подставив значение х_п из (23-10), Тогда получим

Выражение (2442) в таком виде пригодно для вычисления значения сопротивления рассеяния скоса, приведенного к первичной обмотке, причем в множитель перед Х_с в выражениях вида (23-45) необходимо включить обмоточные данные первичной обмотки.

Исисшьзуя формулу (20-3), величину Vkl можно разложить в степенной ряд и при bjx

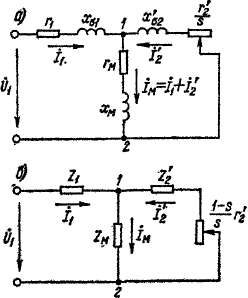
§ 24-4. Схемы замещения асинхронной машины

Т-образная схема замещения. Уравнениям (24-40), как нетрудно видеть, соответствует схема замещения рис. 24-5. Сопротивлением намагничивающей цепи является главное индуктивное сопротивление первичной обмотки, и по этой цепи протекает намагничивающий ток

Напряжение на зажимах 1 я 2 намагничивающей цепи

Схема замещения рис. 24-5 не учитывает магнитных потерь в сердечниках машины.

Потери в сердечнике статора (первичной цепи) могут быть учтены при f_x = const аналогично тому, как это было сделано для трансформатора, путем включения на зажимы / и 2 схемы рис. 24-5 параллельно сопротивлению х_л активного сопротивления г_мг такой величины, что потери в нем будут равны магнитным потерям в сердечнике статора на одну фазу:

Величину г_мг можно найти, если из опытных или расчетных данных известны потери в сердечнике статора р_мг1 при определенном Е_х или определенном магнитном потоке. Обычно г_мг ^> х_т1.

Параллельно включенные сопротивления г_мг и х_п можно объединить в одно общее сопротивление намагничивающей цепи

Рис. 24-5. Т-образная схема замещения асинхронной машины без-учета магнитных потерь

соответствующее механической мощности, развиваемой на роторе машины. Схема рис. 24-6, б аналогична схеме замещения трансформатора, к вторичным зажимам которой подключено нагрузочное сопротивление г’_л2.

Намагничивающий ток схем рис. 24-6 содержит, кроме реактивной составляющей 1_МГ, также активную составляющую /_мй, соответствующую магнитным потерям в статоре:

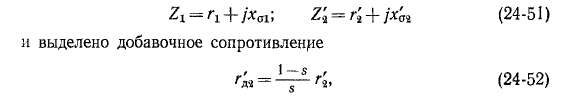
Из приведенных данных видно, что сопротивление намагни* чнвающей цепи схемы замещения асинхронных машин значительно/ меньше, чем у трансформаторов. Это объясняется наличием в маг« яйтной цепи асинхронных машин воздушного зазора между статором и ротором. В связи^с этим надайшчивающий ток Л ток хо-лостбго хода асинхронных машин значительно вышем‘_% *= 0,25-4—!>0,$0), чем у трансформаторов.

Из схем замещения рис, 24-6 можно сделать вывод, чтй ври ymf дичекии /i, т.-е. при увеличении нагрузки мацщны, велйчдаы JEj rsj ф при U = const будут уменьшаться. Однако » пределах’ нормальных рабочих нагрузок изменение потока машины цевеликЗ* я составляет лишь несколько дродентов.

Г-образная схема замещения. Сх«^ы замещения, изобр^жейные на рис. 24-5 и 24-6, хорошо отражают реальныефизически,€ процессы,

Рис 24-6* Т-образные схемы замещения асинхронной машины с учетом магнитных потерь

происходящие в машине, так как при отсутствии скоса пазов напряжение намагничивающей цепи и намагничивающий ток соответствуют реальному потоку основной гармоники поля. Однако для исследования некоторых вопросов эти схемы несколько неудобны, так как их цепи разветвлены и напряжение на зажимах параллельной цепи U_n при и_г — const непостоянно. Более удобной в этом отношении является схема замещения, в которой зажимы параллельной цепи вынесены на первичные зажимы, под напряжение U_x. Из рассмотрения рис. 24-6 и уравнений (24-40) видно, что в подобной схеме сопротивление, соответствующее на рис. 24-6 и в выражениях (24-40) сопротивлению Z_x = г_х + >х_аъ должно быть равно нулю. Для достижения этого равенства необходимо произвести соответствующее преобразование уравнений напряжения машины.

Составим по правилу контурных токов уравнения напряжений схемы рис. 24-6, б:

Уравнения (24-54) и ^24-55) можно получить также из уравнений (24-40), если ввести в них Z_x и Z’₄ из (24-51) и заменять jx_tl на Z_№,

Для преобразования уравнений (24-54) и (24-55) перейдем в них от переменной /£ к новой переменной /£’ по равенству

где С_х — некоторое^ неопределенное пока комплексное число. Эту операцию можно рассматривать как новое приведение вторичной цепи, причем С_х является коэффициентом приведения, а /«’ — новым приведенным током.

Подставим /^ из (24-56) в (24-54) и прибавим и вычтем в лравой части член CiZj_v Тогда^ получим

Очевидно, что последний член (24*57) соответствует намагничивающей, или параллельной, цепи новой схемы замещения. На основании изложенного для получения Г-образной схемы замещения в выражений (24-57) необходимо положить

Ток 1₀₀ представляет собой первичный ток идеального холостого хода асинхронной машины, когда ее ротор вращается с синхронной скоростью (s = 0).

Для этого режима сопротивления схем замещения

в результате чего в этих схемах /^ = /j = 0 и через намагничивающую цепь протекает ток

Так как сопротивление Z_x + Z_M от скольжения s не зависит, то при и_г = const и /_х = const также /₀₀ = const.

При s = О поток статора вращается синхронно с ротором, вследствие чего, естественно, /₂ = 0 и машина не развивает вращающего момента. Поэтому асинхронный двигатель мог бы достичь синхронной скорости (s = 0) на холостом ходу, без нагрузки на валу, только в идеальном случае; когда механические потери, магнитные потери в роторе и добавочные потери, обусловленные зубчатостью ротора, были бы равны нулю и движение ротора не испытывало бы сопротив-ления. Поэтому осуществить этот режим можно только путем приложения к валу постороннего, или внешнего, двигательного вращающего момента.

При реальном холостом ходе асинхронного двигателя скольжение, хотя и весьма мало (доли процента), но все же отлично от нуля.

В схемах замещения рис. 24-7 сопротивления С₁г₁ и С\г’^ уже не являются чисто активными, как и ■ сопротивления С_±х_а1 и С\х’с_ъ не являются чисто индуктивными.

Анализ коэффициента С_г. В соответствии с выражениями (24-50) и (24-51) Cx из (24-58) можно представить в следующем виде:

Мнимая часть С₁ отрицательна, так как обычно г_гх_я > х_а1г_и. Величину Ci можно представить также в показательном виде:

Поскольку мнимая часть С_г обычно отрицательна, то и ее аргумент тоже отрицателен, в связи с чем в показателе (24-64) введен минус. Тогда величина у положительна. В машинах мощностью 8—10 кет и выше у 0) вызывает уменьшение угла у.

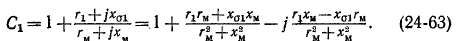
В связи с малостью у мнимая часть коэффициента С_х мала, и поэтому его модуль

Величина С_х имеет простую физическую интерпретацию.

Согласно схемам замещения рис. 24-6 и 24-7,, при идеальном холостом ходе

Рис. 24-8. Векторная диаграмма асинхронной машины при идеальном холостом ходе (s=0)

Таким образом, модуль С\ равен отношению первичного напряжения V_x к первичной з. д. с. Е_г при идеальном хо*; лостом ходе, а аргумент С_г — углу между векторами Oi-u —Ё_х (рис. 24-8).

§ 24-5. Режимы работы, энергетические соотношения и векторные диаграммы асинхронной машины

Двигательный режим (0

Асинхронный двигатель потребляет из сети активную мощность

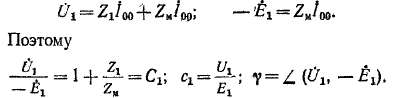
Соотношение (24-74) совпадает с (24-24).

Часть механической мощности Р_мх теряется внутри самой машины в виде механических потерь р_нх (на вентиляцию, на трение в подшипниках и на щетках машин с фазным ротором, если эти щетки при работе не поднимаются), магнитных потерь в сердечнике ротора р_жП и добавочных потерь р_д. Последние вызваны в основном

высшими гармониками магнитных полей, которые возникают ввиду наличия высших гармоник н. с. обмоток и зубчатого строения статора и’ ротора. Во-первых, высшие гармоники поля индуктируют э. д. с. и токи в обмотках, в связи с чем появляются добавочные электрические потери. Эти потери заметны по величине только в обмотках типа беличьей клетки. Во-вторых, эти гармоники поля обусловливают добавочные магнитные потери на поверхности (поверхностные потери) и в теле зубцов (пульсационные потери) статора и ротора. Вращение зубцов ротора относительно зубцов статора вызывает пульсации магнитного потока в зубцах, и поэтому соответствующая часть потерь называется пульсационны-ми потерями. Магнитные потери в сердечнике ротора при нормальных рабочах режимах обычно очень малы и отдельно не учитываются 1 ;

Добавочные потери трудно поддаются расчету и экспериментальному определению. Поэтому, согласно ГОСТ 183—66, их принимают равными 0,5% от подводимой мощности при номинальной нагрузке, а при других нагрузках эти потери пересчитывают пропорционально квадрату первичного тока. Отметим, что в обмотках возникают также добавочные потери от вихревых токов в связи с поверхностными эффектами. Однако эти потери в случае необходимости учитывают соответствующим увеличением сопротивлений г_х и г₂ и поэтому в величину р_д не включают.

Полезная механическая мощность на валу, или вторичная мощность,

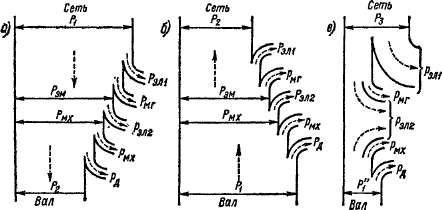
В соответствии с изложенным на рис. 24-9, а изображена энер* гетическая диаграмма асинхронного двигателя. Сумма потерь двигателя

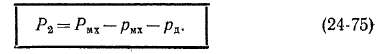
= 0,72 н- 0,95. Более высокие к. п. д. имеют двигатели большей мощности и с большей скоростью вращения.

В качестве иллюстрации приведем данные о потерях и к. п. д. трехфазного асинхронного двигателя с Р_я = 14 кет, и_я _н = = 220/380 в, /_1й = 27,2а (фазный), ^ = 50 гц, 2р = 4, s_H = 0^28, я_н = 1460 об/мин, cos ф_н = 0,877. Для этого двигателя в номинальном режиме работы Р₂ = р^ = 14 000 в/п, р_Эл1 = 770 вт, р_кГ = = 318 вт, р_Эл2 — 411 вт, р_их = 205 вт, р_Й = 79 вт, сумма потерь

Рис. 24-9. Энергетические диаграммы асинхронной машины при работе в режиме двигателя (а), генератора (б) и противовключения (в)

р_ъ = 770 + 318 + 411 + 205 + 79 = 1783 вт. Первичная мощность Р_х = 14 000 + 1783 = 15 783 вт. К- п. д., согласно равенству (24-77),

Рассмотрим еще некоторые вопросы, относящиеся к асинхронным двигателям.

Из выражений (24-71), (24-72) и (24-73) вытекают следующие важные соотношения:

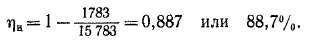
Очевидно, что требование малости s_H сопряжено с требованием, малости г_2:)..

Отметим, что электрическая мощность

развиваемая во вторичной цепи асинхронного двигателя, называется; также мощностью скольжения.

На основе схемы замещения рис. 24-6 можно рассмотреть также баланс реактивных мощностей асинхронного двигателя. Из первичной цепи потребляется реактивная мощность

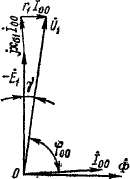
Векторная диаграмма асинхронного двигателя строится на основе схемы замещения рис. 24-6 и имеет вид, изображенный на рис. 24-11, а. Она аналогична векторной диаграмме трансформатора и отличается от нее относительно большей величиной намагничивающего тока /_м и тем, что электрическая нагрузка вторичной цепи, соответствующая механической мощности Р_яЖ, является чисто активной. Ввиду малости скольжения сопротивление r’Js 1 значительно больше х^, и угол ita поэтому мал.

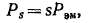
Генераторный режим (— оо

Рис. 24-11. Векторные диаграммы асинхронной машины при работе в режимах двигателя (в), генератора (б) и противовключения (в)

Теоретически скорость п в генераторном режиме может изменяться в пределах п_х s > — оо. В действительности высокие скорости вращения недопустимы по условиям механической прочности, а по условиям ограничения потерь и нагревания и сохранения высокого к. п. д. в генераторном режиме возможны абсолютные значения скольжения такого же порядка, как и в двигательном режиме.

Рассмотрим на основании соотношения (24-17) активные и реактивные относительно э. д. с. £₂ составляющие токи 1_%. Для этого положим в выражении (24-17) й»₂ = Е_г и умножим числитель и знаменатель на сопряженный комплекс знаменателя. Тогда получим

В двигательном режиме s > 0 и обе составляющие 1_га, /_2/. тока /₂ положительны. Множитель — / перед /_2г означает поворот вектора /_2Г относительно /_2О на комплексной плоскости в сторону вращения часовой стрелки на 90°. Это означает, что /_2Г отстает от /_2а на 90°, т. е. /_2г является индуктивным током.

В генераторном режиме s 0, а величина 1_Ы меняет знак, т. е. становится отрицательной и меняет свою фазу на 180°. Физически это объясняется тем, что поле вращается относительно ротора по сравнению с двигательным режимом в обратную сторону, вследствие чего изменяются знаки э. д. с. £_2S и активной составляющей тока /₂. В результате изменяется также знак вращающего момента, т. е. последний действует против направления вращения и становится’ тормозящим.

На основании изложенного на рис. 24-11, б построена векторная диаграмма асинхронного генератора. Вектор первичного тока,

вследствие поворота /^ почти на 180° также поворачивается в сторону вращения часовой стрелки. При этом ц>_х > 90° и

т. е. активные составляющие первичного тока и первичной мощности изменяют знак. Это означает, что машина уже не потребляет,, как в режиме двигателя, а отдает в сеть активную мощность и ак-

рицательно и поэтому величина—— положительна.

Из векторных диаграмм рис. 24-11, а и б следует также, что реактивные составляющие первичного тока

и первичной мощности

при переходе машины из двигательного режима в генераторный сохраняют свои знаки. Это означает, что асинхронный генератор также потребляет из сети реактивную мощность и индуктивный ток. Поэтому асинхронный генератор может работать только на сеть» к которой приключены такие электрические машины и устройства (например, синхронные генераторы или компенсаторы, конденсаторы), которые могут являться источниками реактивной мощности,

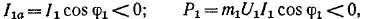
потребляемой асинхронным ренератором для создания в нем магнитного поля или магнитного потока (см. также § 29-2). Потребление асинхронными генераторами реактивной мощности является весьма существенным недостатком, вследствие чего эти генераторы применяются только в очень редких случаях.

Равенства (24-67)—(24-74), (24-78) и (24-79) справедливы также для генераторного режима, если иметь в виду, что в этом режиме s

В генераторном режиме работы сопротивления — и —— г’^

в схемах замещения рис. 24-6 изменяют знак, т. е. становятся отрицательными, что связано также с изменением знаков соответствующих мощностей. Хотя электрические проводники могут иметь только сопротивления г > 0, тем не менее, введение понятия об отрицательных активных сопротивлениях полезно. Если положительные сопротивления г являются потребителями электрической энергии Рг, то отрицательные г необходимо рассматривать как источники, или генераторы, электрической энергии Рг. В частности, генератор постоянного тока в целом можно рассматривать как отрицательное сопротивление

Для ненасыщенного генератора последовательного возбуждения U

I, и для него поэтому г = const. Для других генераторов г =f= const. Отрицательные при s

В соответствии с изложенным на рис. 24-9, б изображена энергетическая диаграмма асинхронного генератора.

Преобразование реактивной мощности в асинхронном генераторе происходит так же, как и в двигателе (рис. 24-10).

Режим противовключения (1 1. На практике в этом режиме обычно 1

Поскольку как в двигательном, так и в режиме противовключения s > 0, то в соответствии’С выражением (24-85) активные и реактивные составляющие вторичного тока имеют в» режиме противовключения такие же знаки, как и в двигательном. Это означает, что и в режиме противовключения машина потребляет из сети активную мощность и развивает положительный вращающий момент,

действующий в сторону вращения поля. Но, поскольку ротор вращается в обратном направлении, на него этот момент действует тормозящим образом.

В режиме лротивовключения машина потребляет также механическую мощность с вала или с ротора, поскольку внешний вращающий момент действует в сторону вращения ротора. Как мощ-н сть, потребляемая из сети, так и мощность, потребляемая с вала, расходуются на потери в машине. Полезной мощности машина поэтому не развивает, а в отношении нагрева рассматриваемый режим является тяжелым.

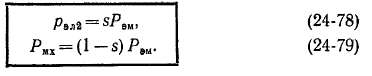
Соотношения (24-67)—(24-76) и (24-78),- (24-79) действительны также и для режима противовключения. При s> 1, согласно выражению (24-71), Р»д>0, а согласно выражению (24-78), р_Эл2 > >^ft,_M. Поэтому получаемая за счет энергии сети и передаваемая на ротор электромагнитная мощность покрывает только часть-потерь во вторичной обмотке. В соответствии с соотношением (24-74) механическая мощность Р_т

и в данном случае Р_вм > 0 и — Р_ях > 0.

На основании изложенного и в соответствии со схемами рис. 24-6; на ряе. 24-9, в, изображена энергетическая диаграмма, а на; рис. 24-11,^ —векторная диаграмма асинхронной машины в pej жиме противовключения. Преобразование реактивной мощносг^ э режиме противовключения происходит так же, как и в двигательном (рис. 24-1(3).

уменьшения скорости вращения. При п да 0 машину необходимо отключить от сети, так как иначе она придет во вращение в обратном направлении. Таким же образом может осуществляться быстрый реверс (изменение направления вращения) двигателя, причем в этом случае, естественно, при п да О отключать двигатель от сети не нужно. В начале процесса реверсирования также существует режим противовключения.

Режим противовключения называют также режимом электромагнитного тормоза. Следует, однако, иметь в виду, что существуют и другие способы электромагнитного торможения асинхронной машины.

Режим короткого замыкания. Режимом короткого замыкания асинхронной машины называется ее режим при s = 1, т. е. при неподвижном роторе. Этот режим соответствует начальному моменту пуска асинхронного двигателя из неподвижного состояния. Сопротивление асинхронной машины относительно ее первичных зажимов при s — 1 называется сопротивлением короткого замыкания Z_K. Согласно схемам замещения рис. 24-6,

Источник