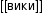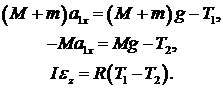Машина Атвуда
Машина Атвуда — лабораторное устройство для изучения поступательного движения с постоянным ускорением. Была изобретена в 1784 году английским физиком и математиком Джорджем Атвудом.
Содержание
Описание
Идеальная Машина Атвуда имеет конструкцию: через блок, укрепленный на некоторой высоте от стола, переброшена нить, к концам которой привязаны два тела с массами 
и 
.
Когда массы тел равны (
) система находится в состоянии безразличного равновесия вне зависимости от положения грузов.
Если 
, тогда вся система тел приходит в поступательное движение.
Формула для нахождения ускорения
Это движение описывается с помощью второго закона Ньютона, представленного в общем виде:
Применительно к нашей задаче для левого и правого тел уравнение движения запишется в виде двух уравнений в проекциях на ось 
:
Мы считаем, что нить идеальна (то есть невесома и нерастяжима) и блок невесом, значит 
и 
, получим:
Формула для нахождения ускорения свободного падения
Измерив время прохождения грузами определённого расстояния, можно вычислить их ускорение. Отсюда:
Формула для нахождения силы натяжения нити
Для нахождения натяжения нити в любое из уравнений подставляем выражение для ускорения, полученное выше. Например, подставляя в первое уравнение системы выражение для ускорения, получаем:
Литература
Ссылки
Полезное
Смотреть что такое «Машина Атвуда» в других словарях:
машина Атвуда — Atvudo mašina statusas T sritis Standartizacija ir metrologija apibrėžtis Tolygiai greitėjančio judesio dėsnių demonstravimo ir tikrinimo įtaisas. Juo nustatoma trinties jėga, patikrinamas antrasis Niutono dėsnis. atitikmenys: angl. Atwood’s… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
машина Атвуда — Atvudo mašina statusas T sritis fizika atitikmenys: angl. Atwood’s free fall apparatus; Atwood’s machine vok. Atwoodsche Maschine, f rus. машина Атвуда, f pranc. machine d’Atwood, f; machine de chute d’Atwood, f … Fizikos terminų žodynas
АТВУДОВА МАШИНА — (от собств. им. физика Атвуда; устроен. в 1784 г.). Прибор, объясняющий законы падения тел. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АТВУДОВА МАШИНА от собственного имени. Физический прибор для определения… … Словарь иностранных слов русского языка
Атвуд, Джордж — Джордж Атвуд George Atwood Род деятельности: физик, математик, изобретатель, шахматист Дата рождения: 1745 год(1745) … Википедия
Лагранжева механика — Классическая механика … Википедия
Суточное вращение Земли — Наклон земной оси по отношению к плоскости эклиптики (плоскости орбиты Земли). Суточное вращение Земли вращение … Википедия
Atvudo mašina — statusas T sritis Standartizacija ir metrologija apibrėžtis Tolygiai greitėjančio judesio dėsnių demonstravimo ir tikrinimo įtaisas. Juo nustatoma trinties jėga, patikrinamas antrasis Niutono dėsnis. atitikmenys: angl. Atwood’s machine vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Atwoodsche Maschine — Atvudo mašina statusas T sritis Standartizacija ir metrologija apibrėžtis Tolygiai greitėjančio judesio dėsnių demonstravimo ir tikrinimo įtaisas. Juo nustatoma trinties jėga, patikrinamas antrasis Niutono dėsnis. atitikmenys: angl. Atwood’s… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Atwood’s machine — Atvudo mašina statusas T sritis Standartizacija ir metrologija apibrėžtis Tolygiai greitėjančio judesio dėsnių demonstravimo ir tikrinimo įtaisas. Juo nustatoma trinties jėga, patikrinamas antrasis Niutono dėsnis. atitikmenys: angl. Atwood’s… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Fallmaschine — Atvudo mašina statusas T sritis Standartizacija ir metrologija apibrėžtis Tolygiai greitėjančio judesio dėsnių demonstravimo ir tikrinimo įtaisas. Juo nustatoma trinties jėga, patikrinamas antrasis Niutono dėsnis. atitikmenys: angl. Atwood’s… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Изучение законов поступательного движения на машине Атвуда: формулы и пояснения
Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Что такое машина Атвуда?
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.
Вам будет интересно: Пространственная экономика: описание специальностей и структура
Вам будет интересно: Что такое подполье? Подпольная организация «Молодая гвардия». Антифашистское движение
Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
Где m – инерционная масса тела, a – ускорение.
Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.
Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
Проверка решения уравнений динамики
Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
Откуда ускорение определяется однозначно:
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
T = (m2*F1 + m1*F2)/(m1 + m2).
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
Механическая конструкция машины Атвуда
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Тверской государственный университет»
Кафедра общей физики
Лабораторная работа №12
Изучение законов движения тел в поле силы тяжести на машине Атвуда
Цель работы: изучение динамики поступательного движения связанной системы тел;
Приборы и принадлежности: машина Атвуда, набор грузов и перегрузков.
Введение
Принцип работы машины Атвуда основан на использовании законов свободного падения тела в воздухе.
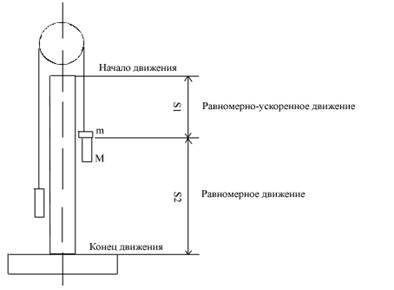
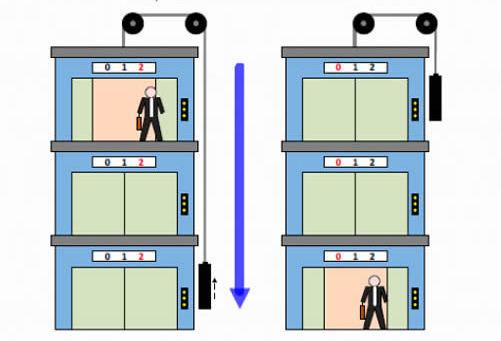
Через ролик, монтированный на подшипнике таким образом, чтобы он мог вращаться с возможно малым сопротивлением, проходит нитка с двумя одинаковыми грузами массой 
каждый. Следовательно, система находиться в равновесии (масса М=60 гр.).
Если на одну сторону блока прибавим небольшой перегрузок массой 
, тогда система – два груза и небольшой перегрузок – получат ускорение под действием перегрузка, и, передвигаясь с ускорением, пройдёт путь 
.
На кольце перегрузок будет отцеплен, и грузы пройдут, теперь уже в равномерном движении, путь 
.
Механическая конструкция машины Атвуда
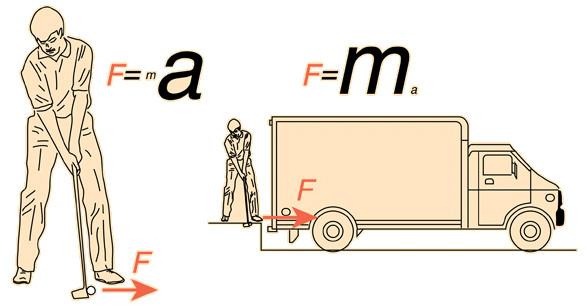
Общий вид машины Атвуда показан на рис.1. На вертикальной колонне /1/, закреплённой в основании, закреплены три кронштейна: неподвижный кронштейн и два подвижных кронштейна – средний /4/ и верхний /5/, а также верхняя втулка /6/.
Основание оснащено регулируемыми ножками, которые позволяют провести выравнивание положения машины.
На верхней втулке, при помощи верхнего диска закреплён узел подшипника ролика, ролик /10/ и электромагнит.
Через ролик проходит нить /12/ с привязанными на её концах грузами /13/ и /14/
Электромагнит, после подведения к нему питающего напряжения, при помощи фрикционной муфты, удерживает систему ролика с грузами в состоянии покоя.
Верхний и средний кронштейны можно перемещать вдоль колонки, фиксировать в любом положении, устанавливая, таким образом, длину пути равномерно-ускоренного и равномерного движения. Для облегчения определения их путей на колонке имеется миллиметровая шкала /15/. Все кронштейны имеют указатель положения, а верхний кронштейн дополнительную черту, облегчающую точное согласование нижней грани верхнего, большего груза с определённым началом пути движения.
На среднем кронштейне закреплён кронштейн /кольцо/ и фотоэлектрический датчик /17/. Кронштейн /кольцо/ снимает с падающего вниз груза дополнительный перегрузок, а фотоэлектрический датчик в это время образует электрический импульс, сигнализирующий начало равномерного движения грузов. Оптическая ось фотоэлектрического датчика /черта на его корпусе/ находится на уровне указателя положения среднего кронштейна.
Нижний кронштейн оснащён двумя кронштейнами с резиновыми амортизаторами, в которые ударяет завершающий своё движение груз, а также фотоэлектрическим датчиком /19/ с оптической осью на уровне указателя кронштейна, после пересечения которого нижней гранью падающего груза образуется электрический сигнал, сигнализирующий прохождение грузами определённого пути.
У основания прибора находиться жёстко прикреплённый к нему миллисекундомер /20/.
 |
| Рис. 2 |
Теоретическая часть
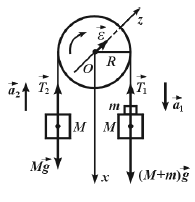
Рассмотрим два груза одинаковой массы М, связанные тонкой нерастяжимой и невесомой нитью, перекинутой через блок радиуса R (рис.2). Если на правый груз поместить перегрузок массой m, то вся система начнёт двигаться равноускоренно. На каждый груз при этом будут действовать две силы – сила тяжести и сила натяжения нити. Запишем второй закон Ньютона для правого груза массы 
и левого груза массы :
(1)
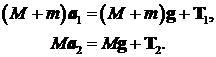
Блок не движется поступательно, а только вращается. Уравнение вращательного движения блока массы 
имеет вид:
. (2)
Здесь 
– момент сил, действующих на блок, 
– момент инерции блока относительно его оси симметрии, 
– угловая скорость вращения блока. На блок действуют сила тяжести, сила реакции, сила трения и две силы натяжения нити 
и 
. Если считать, что сила трения пренебрежимо мала, то из всех сил только силы натяжения нити создают отличный от нуля момент вращения блока относительно его оси симметрии. Вектор угловой скорости и вектор углового ускорения 
направлены вдоль оси 
, совпадающей с осью симметрии блока. Движение же грузов происходит вдоль оси 
. Спроецируем (1) и (2) на эти оси:
(3)
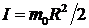
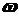
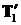
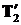
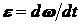
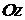
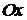
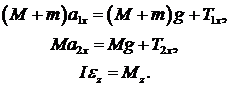
Здесь мы для общности рассмотрения не указываем направление ускорений, хотя из постановки задачи ясно, что правый груз будет двигаться вниз, т.е. проекция его ускорения положительна.
Задание 1. Покажите, что
1. Т.к. нить невесома, то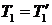 
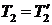
и 
.
2. Момент силы 
относительно оси симметрии блока равен 
, а момент силы 
равен 
.
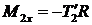
Т.к. нить нерастяжима, то её длина не изменяется. Поэтому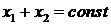 
. Дифференцируя последнее равенство по времени, получим связь скоростей и ускорений грузов
Т.е. ускорения грузов одинаковы по величине. В связи с выше изложенным, уравнения (3) примут следующий вид:
Т.к. нить не проскальзывает по блоку, то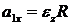 
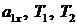
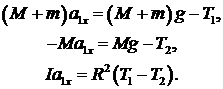
(почему?). В итоге имеем следующую систему из трёх уравнений относительно трёх неизвестных 
:
(4)
Решая систему (4), найдём ускорение грузов (решите систему самостоятельно!):
. (5)
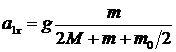
Если массой блока пренебречь, то, во-первых придём к равенству сил натяжения нитей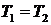 
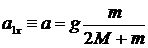
, а во-вторых ускорение грузов станет равным
. (6)
Если нет перегрузка, то, как следует из (5), ускорения грузов равны нулю, т.е. грузы движутся равномерно (и проходят путь ).
Ускорение (6) может быть найдено также из кинематических соображений. Пусть – расстояние, которое проходит груз при равноускоренном движении (до снятия перегрузка, т.е. от белой линии до фотодатчика). К моменту достижения перегрузком среднего кронштейна скорость груза будет удовлетворять следующему соотношению:
. (7)
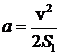
После снятия перегрузка движение груза станет равномерным, поэтому
. (8)
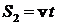
Здесь – это расстояние между средним и нижним кронштейнами; (от фотодатчика среднего кронштейна до фотодатчика нижнего кронштейна), 
– время, регистрируемое миллисекундомером. Из (7) и (8) находим
. (9)
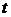
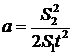
Сравнивая экспериментальное значение для ускорения, найденное по формуле (9), со значением, рассчитанным согласно (6), можно приблизительно проверить выполняемость второго закона Ньютона при движении тел в поле сил земного тяготения.