тренажер для изучения универсального исполнителя
Что это такое?
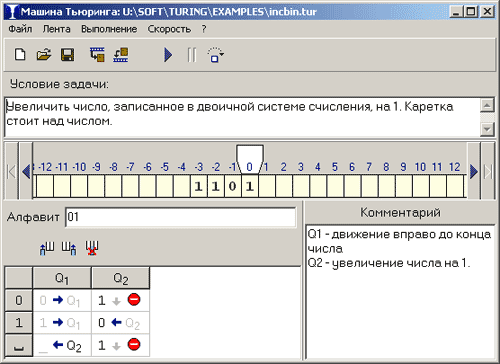
Тренажёр «Машина Тьюринга» — это учебная модель универсального исполнителя (абстрактной вычислительной машины), предложенного в 1936 году А. Тьюрингом для уточнения понятия алгоритма. Согласно тезису Тьюринга, любой алгоритм может быть записан в виде программы для машины Тьюринга. Доказано, что машина Тьюринга по своим возможностям эквивалентна машине Поста и нормальным алгорифмам Маркова.
Машина Тьюринга — это автомат, который управляется таблицей. Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q=
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей:
Использование и скачивание материалов означает, что вы приняли условия этого лицензионного соглашения.
Скачать
Пароль к архиву — kpolyakov.spb.ru
В архив включены следующие файлы:
| turing.exe | основная программа — учебная модель «Машины Тьюринга» |
| EXAMPLES | подкаталог с примерами программ для тренажера «Машина Тьюринга« |
После распаковки архива программа находится в работоспособном состоянии и не требует никаких дополнительных установок.
тренажер для изучения универсального исполнителя
Что это такое?
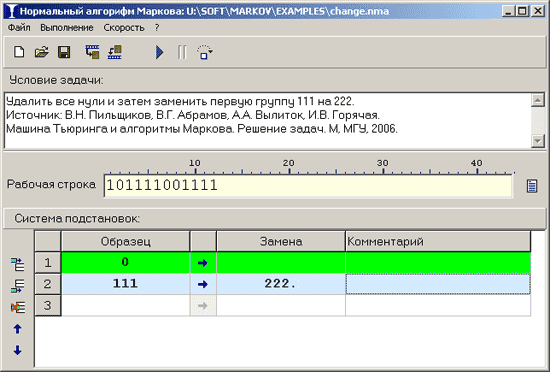
Тренажёр «Нормальные алгорифмы Маркова» — это учебная модель универсального исполнителя, предложенного в 1940-х годах А.А. Марковым для уточнения понятия алгоритма. Марков предположил, что любой алгоритм может быть записан в виде нормального «алгорифма» (учёный считал, что правильно произносить это иностранное слово именно так). Позднее было доказано, что нормальные алгорифмы Маркова эквивалентны по своим возможностям другим универсальным исполнителям: машине Тьюринга и машине Поста.
Нормальный алгорифм задает метод преобразования строк с помощью системы подстановок. Каждая подстановка состоит из слова-образца и слова-замены, разделенных цепочкой символов «->». На каждом шаге замены подстановки просматриваются по порядку сверху вниз, и выполняется первая из них, которая подошла: первое найденное слово-образец рабочей строки заменяется на слово-замену.
Левая часть (слово-образец) может отсутствовать, в этом случае слово-замена ставится в самое начало рабочего слова. Обычно такая замена должна стоять последней в списке подстановок (иначе происходит зацикливание).
Правая часть подстановки тоже может отсутствовать (при стирании образца).
Где почитать ещё?
Что с этим делать?
В верхней части программы находится поле редактора, в которое можно ввести условие задачи в свободной форме.
Система подстановок, задающая нормальный алгорифм Маркова, набирается в виде таблице в нижней части окна программы.
Программа может выполняться непрерывно (F9) или по шагам (F8). Команда, которая сейчас будет выполняться, подсвечивается зеленым фоном. Скорость выполнения регулируется с помощью меню Скорость.
Задачи можно сохранять в файлах и загружать из файлов. Сохраняется условие задачи, исходное слово и система подстановок.
Протокол работы алгоритма, в котором показаны все последовательные замены, вызывается при нажатии клавиш Ctrl+P.
Если вы заметили ошибку или у вас есть предложения, замечания, жалобы, просьбы и заявления, пишите.
Технические требования
Программа работает под управлением операционных систем линейки Windows на любых современных компьютерах.
Лицензия
Программа является бесплатной для некоммерческого использования. Исходные тексты программы не распространяются.
Программа поставляется «as is», то есть, автор не несет никакой ответственности за всевозможные последствия ее использования, включая моральные и материальные потери, вывод оборудования из строя, физические и душевные травмы.
При размещении программы на других веб-сайтах ссылка на первоисточник обязательна.
Использование и скачивание материалов означает, что вы приняли условия этого лицензионного соглашения.
Скачать
Пароль к архиву — kpolyakov.spb.ru
В архив включены следующие файлы:
| markov.exe | основная программа — учебная модель «Нормальные алгорифмы Маркова» |
| EXAMPLES | подкаталог с примерами программ для тренажера «Нормальные алгорифмы Маркова« |
После распаковки архива программа находится в работоспособном состоянии и не требует никаких дополнительных установок.
Эмулятор машины Тьюринга
Как пользоваться эмулятором
Что такое машина Тьюринга?
Машина Тьюринга — абстрактная вычислительная машина, предложенная Аланом Тьюрингом для формализации понятия алгоритма. Устройство МТ состоит из следующий частей:
Бесконечная лента
Обычно на ленту в начале работы помещают входное слово. В процессе работы машины Тьюринга содержимое ленты модифицируется устройством управления и в результате на ленте остаётся выходное слово.
Считывающая/записывающая головка
В каждой машине Тьюринга есть специальная головка, указывающая на одну определённую ячейку на ленте. Данное устройство позволяет считывать символ с ячейки, над которой находится, или записывать символ в эту ячейку. Также головка может перемещаться влево и вправо на одну ячейку, или оставаться на месте.
Устройство управления
Допускаются краткие записи для правил:
Примеры машин Тьюринга
Пример 1 (загрузить в эмулятор). К двоичному числу прибавить 1. В начальный и конечный момент головка должна находиться на самом старшем бите слова (слева).
Так как изначально по условию головка МТ находится на самом старшем бите, а увеличивать надо младший, необходимо сначала переместить головку на младший бит, что выполняется в состоянии q0: как только лента увидит символ λ, она сдвинется влево (на младший бит) и перейдёт в состояние икремента (q1).
В состоянии q1 возможны следующие ситуации:
Состояние q2 нужно лишь для выполнения условия остановки головки на старшем бите. Оно полностью аналогично начальному состоянию, только движение происходит в левюу сторону и при достижении пустого символа головка сдвигается вправо и выполняется останов.
Пример 2 (загрузить в эмулятор). В слове из алфавита
| Q \ A | a | b | λ |
|---|---|---|---|
| q0 | b R q0 | a R q0 | ! |
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.
Навигация
Календарь
Машина Тьюринга. Задачи и решения
Один из важнейших вопросов современной информатики — существует ли формальный исполнитель, с помощью которого можно имитировать любого формального исполнителя. ответ на этот вопрос был получен почти одновременно двумя выдающимися учеными — А. Тьюрингом и Э. Постом. Предложенные ими исполнители отличались друг от друга, но оказалось, что они могут имитировать друг друга, а главное — имитировать работу любого формального исполнителя.
Что такое формальный исполнитель? Что значит — один формальный исполнитель имитирует работу другого формального исполнителя? Если Вы играли в компьютерные игры — на экране объекты беспрекословно подчиняются командам играющего. Каждый объект обладает набором допустимых команд. В то же время компьютер сам является исполнителем, причем не виртуальным, а реальным. Вот и получается, что один формальный исполнитель имитирует работу другого формального исполнителя.
Рассмотрим работу Машины Тьюринга.
Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.
Таким образом Машина Тьюринга формально описывается набором двух алфавитов:
A=
Q=
Каждая ячейка ленты может содержать символ из внешнего алфавита A =
Допустимые действия Машины Тьюринга таковы:
1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)
2) сместиться в соседнюю ячейку
3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q
Машина Тьюринга — это автомат, который управляется таблицей.
Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q =
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· направление перемещения: «>» (вправо), «
Поляков информатика машина тьюринга
Один из важнейших вопросов современной информатики — существует ли формальный исполнитель, с помощью которого можно имитировать любого формального исполнителя. ответ на этот вопрос был получен почти одновременно двумя выдающимися учеными — А. Тьюрингом и Э. Постом. Предложенные ими исполнители отличались друг от друга, но оказалось, что они могут имитировать друг друга, а главное — имитировать работу любого формального исполнителя.
Что такое формальный исполнитель? Что значит — один формальный исполнитель имитирует работу другого формального исполнителя? Если Вы играли в компьютерные игры — на экране объекты беспрекословно подчиняются командам играющего. Каждый объект обладает набором допустимых команд. В то же время компьютер сам является исполнителем, причем не виртуальным, а реальным. Вот и получается, что один формальный исполнитель имитирует работу другого формального исполнителя.
Рассмотрим работу Машины Тьюринга.
Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.
Таким образом Машина Тьюринга формально описывается набором двух алфавитов:
A=
Q=
Каждая ячейка ленты может содержать символ из внешнего алфавита A =
Допустимые действия Машины Тьюринга таковы:
1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)
2) сместиться в соседнюю ячейку
3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q
Машина Тьюринга — это автомат, который управляется таблицей.
Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q =
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· направление перемещения: «>» (вправо), «