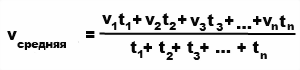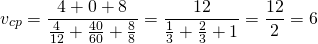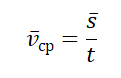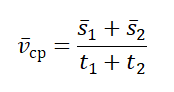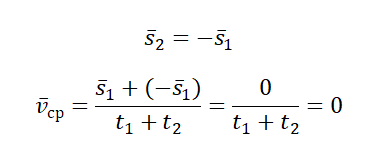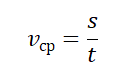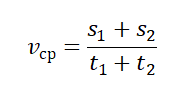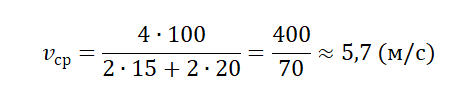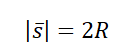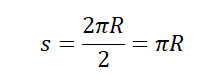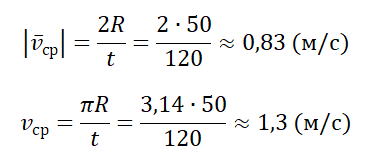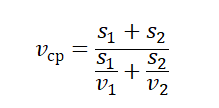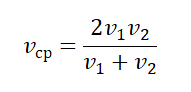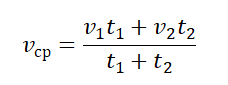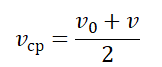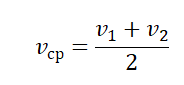Формула нахождения значений скорости, времени и расстояния
С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.
Как же рассчитать скорость?
На самом деле, рассчитать ее можно несколькими способами:
Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.
Теперь нужно подставить имеющиеся значения вместо буквенных символов:
v=100 км/1,5 ч=66,66 км/ч
Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.
Таким нехитрым способом можно найти скорость через время и расстояние.
А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:
Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:
Можно записать использовать и такой вид вычислений:
Но можно записать эту же формулу и в более точном варианте:
Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.
Другие способы вычисления
Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Видео
В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.
Как находить среднюю скорость
Повторим, как находить среднюю скорость, и рассмотрим конкретные примеры.
Чтобы найти среднюю скорость, надо:
1) найти весь пройденный путь;
2) найти все время движения;
3) весь пройденный путь разделить на все время движения:
На примерах посмотрим, как находить среднюю скорость.
1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.
Находим весь пройденный путь: 2∙7 + 3∙5 = 29 км.
Находим все время движения: 2+3=5 часов.
Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.
2) Автомобиль проехал 2 часа по шоссе со скоростью 100 км/ч, 1,5 часа по грунтовой дороге со скоростью 40 км/ч и 30 минут по проселочной дороге со скоростью 26 км/ч. Найти среднюю скорость автомобиля на всем пути.
Переведем минуты в часы: 30 минут = 0,5 часа.
Найдем весь пройденный автомобилем путь:
2∙100 + 1,5∙40 + 0,5∙26 = 200 + 60 + 13= 273 км.
Находим все время движения:
Чтобы найти среднюю скорость движения автомобиля, разделим весь пройденный путь на все время движения:
3) Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.
Найдем весь путь велосипедиста:
3∙12 + 1∙0 + 2∙9 = 54 км.
Найдем все время движения:
Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:
195 Comments
самый лучший сайт по математике спасибо огромное
Илья, спасибо за теплые слова!
Велосипедист проехал со скоростью 12 км/ч 4 км,остановился на 40 мин и продолжил движение со скоростью 8 км/ч и проехал 8 км. Найдите скорость велосипедиста на протяжении всей дороги? Пожалуйста,помогите,очень важно
Валерий, эта задача — на движение по водному пути. Но ее можно решить логически.
Поскольку известно, что скорость катера по течению реки в два раза больше скорости против течения, при этом расстояние туда и обратно — одинаковое, то время, затраченное катером на путь по течению, в два раза меньше времени против течения (скорость и время — обратно пропорциональные величины. Если скорость увеличить в несколько раз, то при том же расстоянии время уменьшится во столько же раз).
Таким образом, все время можно разделить на 3 части, одну часть которого катер потратил на путь по течению, две — на путь против течения. Так как на весь путь было потрачено 2 часа=120 минут, то из них на путь по течению — 1/3 от 120 — это 40 минут=2/3 часа. Чтобы найти скорость, надо расстояние разделить на время: 20:(2/3)=30 км/ч — это скорость катера по течению. Она в два раза больше скорости против течения, следовательно, скорость против течения 30:2=15 км/ч.
Девушка ехала на работу со средней скоростью 40 миль в час, обратно домой ехала со средней скоростью 30 миль в час, весь путь от дома до работы и обратно занял 1 час, сколько миль проехала девушка?
Это — задача на движение. Пусть на работу девушка ехала х часов,тогда обратный путь занял у нее (1-х) часов. По формуле пути путь на работу равен 40х миль, обратный путь — 30(1-х) миль. Так как туда и обратно девушка проехала одинаковое расстояние, составляем уравнение: 40х=30(1-х). Отсюда х=3/7, путь на работу 40∙(3/7)=120/7 миль, туда и обратно — 2∙(120/7)=240/7=38 2/7 мили.
Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Среднее арифметическое
Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.
Обозначим среднее арифметическое буквой « m ». По определению выше найдем сумму всех чисел.
Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.
В итоге мы получаем формулу среднего арифметического:

Для чего нужно среднее арифметическое?
Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.
Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой цене вам продавать мячи.
Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены в магазинах и составим таблицу.
| Магазин | Цена футбольного мяча |
|---|---|
| «Спорт-товары» | 290 руб. |
| «Adidas» | 360 руб. |
| «Все для футбола» | 310 руб. |
Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?
Если выбрать самую низкую ( 290 руб.), то мы будем продавать товар себе в убыток. Если выбрать самую высокую ( 360 руб.), то покупатели не будут приобретать футбольные мячи у нас.
Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.
Вычислим среднее арифметическое цен на футбольные мячи:
Таким образом, мы получили среднюю цену ( 320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не слишком дорого.
Средняя скорость движения
Со средним арифметическим тесно связано понятие средней скорости движения.
Наблюдая за движением транспорта в городе, можно заметить, что машины, то разгоняются и едут с большой скоростью, то замедляются и едут с маленькой скоростью.
Таких участков на пути следования автотранспорта бывает много. Поэтому для удобства расчётов, используют понятие средней скорости движения.
Средняя скорость движения — это весь пройденный путь разделить на всё время движения.
Рассмотрим задачу на среднюю скорость.
Задача № 1503 из учебника «Виленкин 5 класс»
Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец 0,3 ч по просёлочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всём пути.
Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем, и всё время, которое автомобиль двигался.
S1 = 90 · 3,2 = 288 (км) — шоссе.
S2 = 45 · 1,5 = 67,5 (км) — грунтовая дорога.
S3 = 30 · 0,3 = 9 (км) — просёлочная дорога.
S = 288 + 67,5 + 9 = 364,5 (км) — весь путь, пройденный автомобилем.
t = 3,2 + 1,5 + 0,3 = 5 (ч) — всё время.
Vср = 364,5 : 5 = 72,9 (км/ч) — средняя скорость движения автомобиля.
Ответ: Vср = 72,9 (км/ч) — средняя скорость движения автомобиля.
Способы нахождения средней скорости в физике
Основные понятия и законы кинематики
Кинематика — раздел механики, описывающий механическое движение тел без рассмотрения причин, из-за которых происходит движение.
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Для описания движения нужна система отсчета, относительно которой мы будем описывать движение.
Система отсчета — это система координат, связанная с телом отсчета и прибор для измерения времени.
Тело отсчета — это тело, относительно которого рассматривают положение других тел.
Материальная точка — это тело, размеры которого можно не учитывать при решении задачи.
Траектория — это мысленная линия в пространстве, которую при движении описывает материальная точка.
Траектория движения делится на два типа:
Путь — это длина траектории, которую описывает тело или материальная точка за данный промежуток времени.
Перемещение S → — это вектор, соединяющий начальное положение тела или материальной точки с ее конечным положением.
Скорость — это векторная физическая величина, характеризующаяся направлением и быстротой перемещения материальной точки.
Определение средней скорости
Рассчитать среднюю скорость можно по следующей формуле:
Определение средней путевой скорости
Средняя путевая скорость — это отношение пути или длины траектории, пройденного телом, к интервалу времени, за которое этот путь был пройден.
Формула средней путевой скорости выглядит так:
Примеры решения задач
Автомобиль первый час ехал со скоростью 100 км/ч, после чего сделал остановку. Следующие два часа автомобиль ехал со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость на протяжении всего пути автомобиля.
В условии сказано о трех участках пути.
ϑ с р → = S 1 → + S 2 → + S 3 → t 1 + t 2 + t 3
Участки пути мы можем вычислить и посчитать следующим образом:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
ϑ с р = 100 + 180 + 160 1 + 2 + 2 = 440 5 = 88 к м ч
Ответ: средняя скорость составляет 88 км/ч.
Автомобиль проехал по дороге расстояние 140 км за время, равное 2 часам, затем сделал остановку. После остановки автомобиль проехал 60 км за 3 часа. Какова средняя скорость автомобиля за весь путь?
ϑ с р → = ∆ S → ∆ t ϑ с р → = S 1 → + S 2 → t 1 + t 2 ϑ с р → = 140 + 60 2 + 3 = 40 к м ч
Ответ: средняя скорость автомобиля составляет 40 км/ч.
Человек занимается бегом и за 2 часа пробежал 5 км, а за следующий час пробежал 3 км. Определите среднюю скорость бегуна.
Искать среднюю скорость будем как во второй задаче.