Радиус качения шины, скорость и КПП
Данный пост посвящён рациональному выбору ряда КПП и размера шин для достижения максимально возможной скорости на примере ЛГЛ со штатным мотором и фильтром нулевого сопротивления.
Справочная информация
Штатная КПП Лады имеет следующие передаточные числа:
● ГП n0 = 63/17 = 3.706 или = 63/16 = 3.938 (на АМТ 1.0 только 3.7, на АМТ 2.0 поставили 3.9, на МКПП бывает 3.9)
● передачи n1 = 40/11 = 3.636, n2 = 39/20 = 1.950, n3 = 38/28 = 1.357, n4 = 32/34 = 0.941, n5 = 29/37 = 0.784
1. Взаимосвязь скорости автомобиля и частоты вращения коленвала
Тут всё просто, и я уверен, что многим хорошо известно. Приведу это в качестве напоминания.
Скорость v автомобиля вычисляется по формуле:
v = ω∙R/(n0∙ni), (1)
где
v — скорость, м/c;
ω — круговая частота вращения коленвала, рад/с;
R — эффективный радиус качения колеса, м;
n0 — ГП, ni — i-ая передача.
Что такое радиус качения колеса и чем он отличается от внешнего радиуса R0 шины?
Допустим, шины имеют размер 195/55-15″ (у моих шин именно такой размер). Тогда внешний радиус шины можно приблизительно вычислить по формуле:
R0 = 195мм∙55%+15″/2 = 297.75 мм.
Почему приблизительно?
Да потому, что профиль шины не абсолютно точно равен 55% её ширины. Имеется определённый допуск, а отклонение может составлять 1%. Например, Nankang NS-2 и Toyo CF2 имеют R0 = 297.5 мм, что почти не отличается от теоретического значения, а вот у Toyo T1-R R0 = 296.5 мм (хотя и тут различие относительно мало).
Почему мы не можем подставить R0 в формулу (1) для скорости?
Дело в том, что шина под нагрузкой деформируется. Общая деформация шины складывается из деформации боковины и деформации протектора. Это приводит к уменьшению её радиуса R качения.
Как определить радиус качения?
Всё просто, достаточно выразить R из формулы (1):
Пример 1.
Я провёл эксперимент и выяснил, что если ехать на 5-ой передаче и установить на круиз-контроле скорость v = 76 км/ч (по GPS), то обороты двигателя составят ω = 2020 об/мин (при этом давление в шинах 2.1 атм). Используя формулу (2), для моих достаточно подстёртых передних шин Continental CPC5 получаем:
Относительная разница с теоретическим значением составляет:
Это показательный пример, и полученной величиной δR можно пользоваться при практических расчётах.
2. Оценка максимально возможной скорости автомобиля
При больших скоростях движения технически исправного автомобиля с правильно накачанными шинами основная сила сопротивления является силой Fx лобового сопротивления. Она вычисляется по формуле:
Fx(v) = Cx∙½ρ∙v²∙S, (3)
где
Cx — безразмерный коэффициент лобового сопротивления,
ρ — плотность воздуха (зависит от температуры), кг/м³,
S — характерная площадь (площадь миделя), м².
Что происходит с автомобилем во время движения?
Двигатель совершает работу. Работа, совершаемая двигателем за единицу времени, характеризуется его мощностью N(ω), которая есть непостоянная величина и зависит от оборотов коленвала.
На что расходуется мощность двигателя?
С одной стороны, она идёт на увеличение кинетической энергии автомобиля. С другой стороны, часть мощности расходуется на преодоление сил сопротивления. Как известно, мощность — это произведение силы на скорость, поэтому мощность сил лобового сопротивления вычисляется по формуле:
Здесь самое важное, что мощность сил лобового сопротивления пропорциональна кубу (!) скорости:
До каких пор автомобиль может разгоняться?
До тех пор, пока мощность двигателя не сравняется с мощностью всех сил сопротивления, ведь в этом случае у мотора не остаётся резервов для изменения кинетической энергии автомобиля, т.е. для изменения его скорости.
Пример 2.
Ещё один эксперимент, который я провёл, заключался в определении максимальной скорости моего автомобиля (у меня мотор штатный, кроме ФНС). Её величина составила V = 201 км/ч.
Что мы можем из этого выяснить?
Во-первых, при этой скорости достигается баланс мощностей:
Во-вторых, этот баланс достигается на оборотах:
Есть ли у мотора резервы для увеличения максимальной скорости?
Да, есть, ведь максимальная мощность моторов 21127 и 21129 достигается при частоте ωmax = 5800 об/мин.
На сколько можно увеличить максимальную скорость?
Чтобы это вычислить, нужно, используя (5), составить пропорцию:
Из ПТС известно, что максимальная мощность Гранты составляет N(ωmax) = 78 кВт. Судя по ВСХ моторов 21127 и 21129 их мощность при частоте ω = 5340 об/мин составляет N(ω) = 73 кВт. Конечно, это приблизительная величина, для более точных значений можно было бы воспользоваться каким-нибудь Android-приложением измерения мощности автомобиля (например, Torque или PerfExpert). При этом надо пользоваться не абсолютными значениями мощности, а составлять пропорцию подобно (7).
В результате можно сказать, что для ЛГЛ со штатным мотором максимально достижимая скорость равна:
3. Подбор ряда КПП и размера шин
Задача состоит в том, чтобы при частоте коленвала ωmax = 5800 об/мин скорость автомобиля составляла Vmax = 205 км/ч.
Снова преобразуем формулу (1):
и введём обозначение
В случае максимальной скорости:
На текущих шинах и КПП это значение равно:
что очень много, т.е. мы имеем «длинную» трансмиссию и «высокие» шины.
Что будет, если уменьшить размер шин, не меняя при этом ряд КПП?
Изменим только профиль шин на более низкий, т.е. возьмём шины 195/50-15″. Вычислим их радиус качения с учётом поправки δR:
Тогда на штатной КПП
т.е. мы стали ближе к rmax, а, следовательно, максимальная скорость стала ближе к максимально достижимой скорости.
Что будет, если изменить ряд КПП, не меняя при этом размера шин?
Заменим только ГП с 3.7 на более короткую 3.9. Тогда на текущих высоких шинах 195/55-15″ получим
т.е. мы попали в точку, и ЛГЛ с такой ГП будет разгоняться до 205 км/ч.
Поговорим о шинах. Часть 1. Геометрия.
Сегодня я хотел бы поговорить о шинах. Да именно так «о шинах» в очень общем смысле.
Причиной написания этой статьи стал тот факт, что очень часто в последнее время я сталкиваюсь с непониманием автолюбителями того как работает шина и какие параметры на что влияют. Я не претендую на звание очень большого эксперта в шинных вопросах (да я не работаю в шинном НИИ), но все свои выводы в данной статье я постараюсь основывать на каких-то серьезных исследования, школьной физике, информации предоставляемой производителями шин и других источниках и методах анализа, которые не требуют обширного опыта в исследованиях шин или каких-нибудь сложных и специфичных методов анализа. Некоторые примеры, используемые в данной статье, покажутся читателю слишком утрированными и гипертрофированными, но выбраны они не случайно, а для того, чтобы обращаться к ярким воспоминаниям и ощущениям, встречающимся в повседневном опыте большинства читателей.
Данная статья постарается охватить большинство параметров современных шин: от геометрии до свойств материала. Будут показаны некоторые принципы работы тех или иных частей шины. На основе этих принципов будут приведены качественные зависимости параметров поведения автомобиля (разгон, торможение, критическая скорость аквапланирования). Количественные же зависимости зависят от многих параметров и их взаимного влияния, а также от конкретной модели шины, модели авто и его настроек, поэтому выявление конкретного численного эффекта от изменения того или иного параметра возлагается уже на читателя.
Давайте же начнем. И начнем с самого верхнего уровня детализации шины – с ее геометрических параметров.
1. Влияние геометрических параметров на характеристики движения.
1.1 Внешний радиус шины.
Внешний радиус шины, а точнее я бы сказал колеса имеет сильное влияние на разгон, максимальную скорость и комфорт движения. Каким же образом.
Чем меньше диаметр колеса, тем меньше рычаг у силы трения колеса о дорогу, а, следовательно, момент этой силы, противодействующий крутящему моменту, приходящему от двигателя, будет меньше, и значит автомобиль будет разгоняться быстрее. Также на разгон положительно влияет и уменьшающийся с радиусом угловой момент инерции колеса, т.е. колесо меньшего радиуса меньше сопротивляется разгону само по себе, так как его масса сосредоточена ближе к оси вращения. Но за разгон надо платить, и платить приходится максимальной скоростью – при том же количестве оборотов колеса, автомобиль с колесами меньшего диаметра пройдет меньшее расстояние из-за меньшей длины окружности такого колеса, а, значит, и скорость его на тех же оборотах будет ниже. Две эти зависимости довольно очевидны и очень ощутимы.
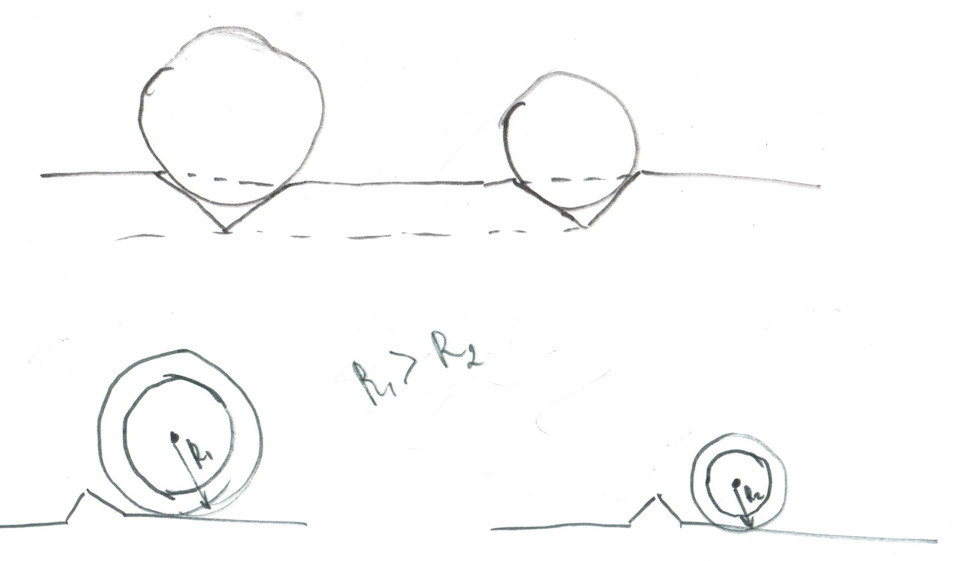
А вот для разговора о комфорте потребуется картинка. На рисунке 1 показаны две шины разного внешнего диаметра. На верхнем рисунке показано поведение шин во время проезда углубления. Видно, что шина большего диаметра провалится меньше в углубление за счет своей меньшей кривизны, а значит ход подвески при отработке этой неровности колесом большего диаметра будет меньше.
На нижнем рисунке показан момент наезда на выступающее препятствие. Поверхность шины большего диаметра будет соприкасаться с неровностью под меньшим углом, в силу того, что точка соприкосновения с препятствием в большом колесе расположена значительно ниже центра колеса чем в маленьком. Это приводит к тому, что горизонтальная составляющая силы взаимодействия колеса и препятствия будет меньше, а, следовательно, и толчок при наезде будет меньше. Вертикальное перемещение в обоих случаях будет одинаковым, так как определяется высотой неровности. Схожий с описанным эффект возникает при сравнении наезда на неровность с крутым краем и с пологим – толчок (точнее клевок) при наезде на неровность с угловатым краем значительно сильнее, правда, в этом примере разность углов соприкосновения поверхностей неровности и колеса достигается не за счет радиуса, а за счет геометрии неровности.
Из фактов, приведенных выше, получаем, что шина большего внешнего радиуса имеет тенденцию быть более комфортной.
1.2 Высота профиля резины. (В этом пункте я буду использовать АБСОЛЮТНУЮ высоту профиля резины, а не относительную, так как так удобнее сравнивать ее с какими-то характерными высотами)
1.3 Ширины шины.
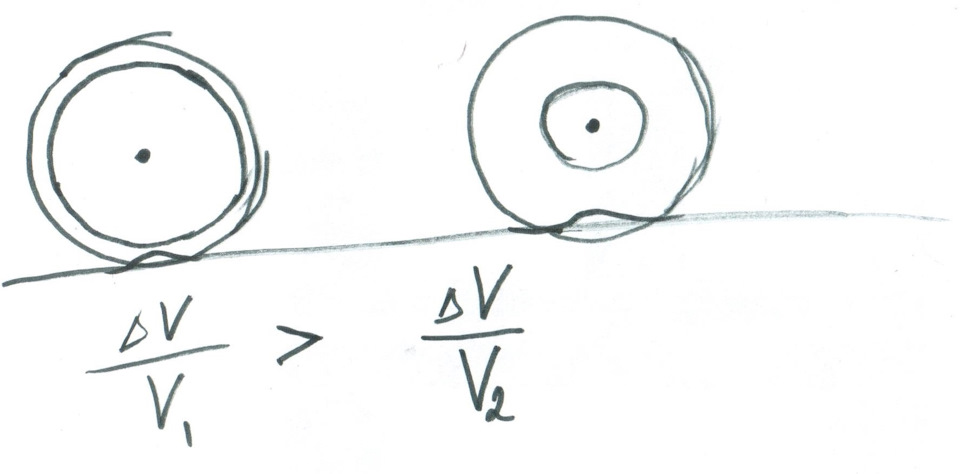
Да, действительно, более широкая шина имеет большее сопротивление качению, как раз таки из-за того, что она имеет изначально внутри больший объем воздуха, чем узкая и, из-за эффекта меньшей относительной деформации при одинаковой неровности, будет мягче более узкой резины. Что, казалось бы, должно положительно сказаться на комфорте, но вот в чем проблема – широкая шина может собрать больше неровностей, чем узкая, просто потому что она захватывает больше дорожного полотна, но это уже очень скользкая зависимость, и определяется она скорее состоянием дороги, а не параметрами шины.
Вот на что ширина сильно влияет, так это на «зацеп» большинству очевидно, что чем шире шина, тем лучше она держится за дорогу, как при разгоне/торможении, так и в поворотах, поэтому шины спортивных автомобилей значительно шире шин гражданских авто. (О природе этого необычного, с точки зрения школьной физики явления, я буду говорить значительно позже – когда буду рассматривать свойства самого материала шины).
Что такое коэффициент сопротивления качению
Чтобы колесо автомобиля катилось, ему надо преодолевать четыре силы: силу тяжести, трение о дорожное полотно, сопротивление воздуху и качению. На преодоление этих сил может приходиться до 30% мощности двигателя грузового автомобиля. У легковых авто такие потери меньше, но даже относительно небольшое снижение этого показателя приводит к уменьшению расхода топлива и увеличению пробега на одном баке.
Что такое сопротивление шин качению
При вращении шина деформируется в пятне контакта с дорожным покрытием, а это приводит к следующим последствиям:
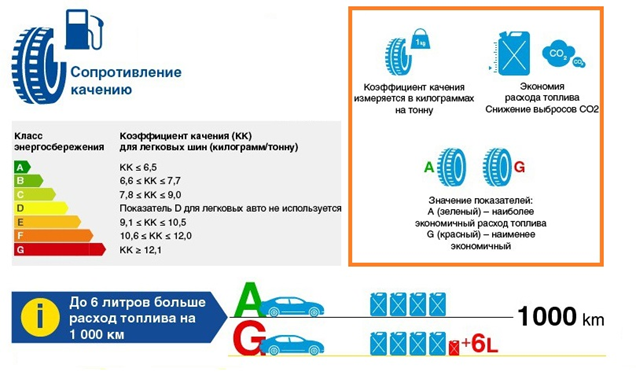
С 2012 г. все шины, продаваемые на территории Евросоюза, обязаны были иметь стикер, на котором цветовой шкалой и буквенной символикой от A (зеленый цвет) до G (красный цвет) указывалась маркировка топливной экономичности. А топливная экономичность каждого класса измерялась коэффициентом сопротивления качению: у шин с маркировкой A он минимальный (RR6.5), у шин с маркировкой G – максимальный (RR12.1).
С мая 2021 года стикер немного изменился, и теперь он содержит не 7, а 5 классов от A до E. И расход топлива между соседними классами по сравнению с предыдущей версией увеличился приблизительно на 0.1 л/100 км.
От чего зависит сопротивление качению
На качение влияют разные факторы. Значительная часть относится к особенностям самой шины и ее состоянию:
На качение влияют и внешние факторы. К ним относятся:
Расчет коэффициента сопротивления качению
Сопротивление качению зависит от массы транспортного средства и коэффициента трения с дорожным покрытием. Силу сопротивления в общем виде рассчитывают по простой формуле:
P = Q*f,
где f – коэффициент трения.
Естественно, что коэффициент трения зависит от типа дорожного покрытия и вида движителя. И у машин с эластичными шинами он ниже, чем у тракторов и вездеходов на гусеничном ходу, но выше, чем у рельсового транспорта.
Размерность этого коэффициента выражается как enkg/t (кг/т). И если RR=12, то это означает, что на каждую тонну автомобиля надо приложить усилие в 12 кг (приблизительно 120 Н), чтобы преодолеть сопротивление качению.
Особенности шин с пониженным сопротивлением качению
Для повышения топливной эффективности производители применяют следующие решения:
Но снижение сопротивления качению не является самоцелью — тестовые испытания «зеленых» шин показывают, что путь торможения у них, как правило, больше, чем у «красных» покрышек. Поэтому важна сбалансированность топливной эффективности и сцепных свойств, экономичности и функциональности.
Рулевые шины имеют четкие реакции при проведении маневра, ведущие — отвечают за сцепление с дорогой и тормозной путь, свободного качения — имеют минимальный коэффициент сопротивления качению и отвечают за экономию топлива.
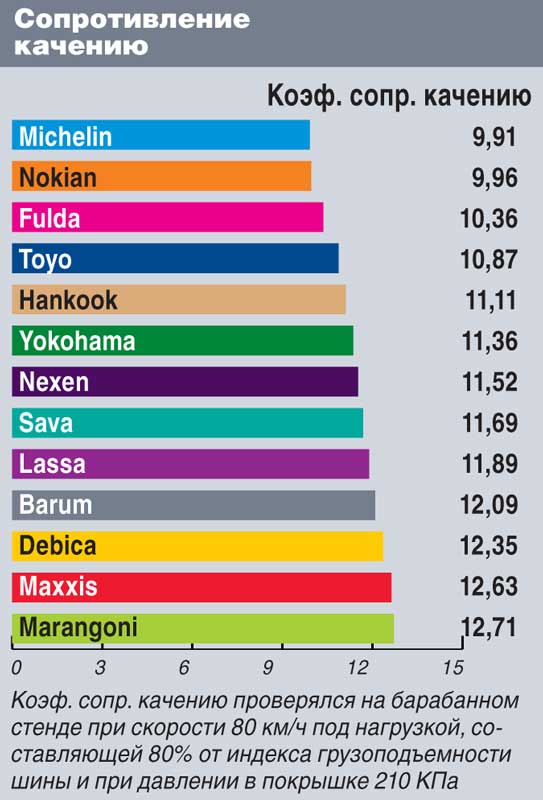
Таблица сопротивления качению разных видов шин:
Заключение
Шины с низким коэффициентом сопротивления качению не только экономят для владельца топливо, они имеют больший пробег и уменьшают выброс выхлопных газов. А это в итоге снижает вредное влияние на экологию.
Полезное видео
Качение шины
Радиус качения
При качении шина подвергается действию центробежных сил. Величина центробежных сил зависит от скорости качения, массы и размеров шины. Под действием центробежных сит шина несколько увеличивается по диаметру. Испытания показали, что при качении шины со скоростью 180—220 км/ч высота профиля увеличивается на 10—13% (результаты испытаний шин на шоссейно-кольцевых мотоциклетных гонках).
Одновременно действие центробежных сил вызывает (за счет увеличения радиальной жесткости шины) некоторое увеличение расстояния от оси колеса до опорной поверхности (плоскости дороги) с одновременным уменьшением площади контакта шины с дорогой. Это расстояние называется динамическим радиусом шины Rо, который больше, чем статический радиус Rс, т. е. Rо>Rc.
Однако при эксплуатационных скоростях движения Rо, практически равен Rс.
Радиусом качения называется отношение линейной скорости движения колеса к угловой скорости вращения колеса:
где Rк — радиус качения, м;
V — линейная скорость, м/с;
w — угловая скорость, рад/с.
Сопротивление качению
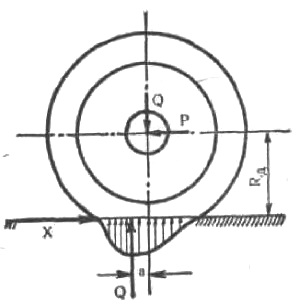
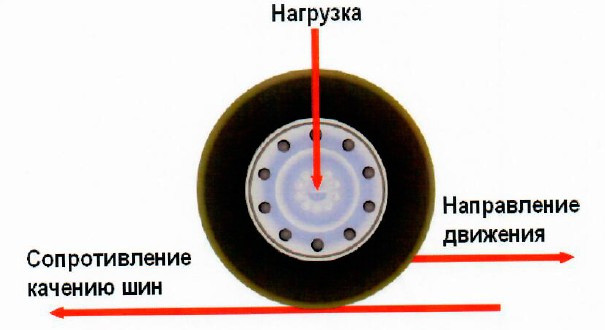
Рис. Качение шины по твердой поверхности
При качении колеса по твердой поверхности каркас шины подвержен циклическим деформациям. При входе в контакт шина деформируется и прогибается, а при выходе из контакта — восстанавливает свою первоначальную форму. Энергия деформации шины, образующаяся при входе элементов в контакт с поверхностью, расходуется на внутреннее трение между слоями каркаса и проскальзывание в зоне контакта. Часть этой энергии превращается в тепло и передается окружающей среде. Вследствие потерь механической энергии скорость восстановления первоначальной формы шины при выходе элементов шины из контакта меньше скорости деформации шины при входе элементов в контакт. В силу этого нормальные реакции в зоне контакта несколько перераспределяются (по сравнению с неподвижным колесом) и эпюра распределения нормальных сил принимает вид, как показано на рисунке. Равнодействующая нормальных реакций, равная по величине радиальной нагрузке на шину, перемещается вперед по отношению к вертикали, прохооящей через ось колеса, на некоторую величину а («снос» радиальной реакции).
Момент, создаваемый радиальной реакцией относительно оси колеса, называется моментом сопротивления качению:
При условии установившегося движения (при постоянной скорости качения) ведомого колеса действует момент, уравновешивающий момент сопротивления качению. Этот момент создается двумя силами — толкающей
силой Р и горизонтальной реакцией дороги X:
М = XRд = PRд,
где Р — толкающая сила;
X — горизонтальная реакция дороги;
Rд — динамический радиус.
PRд = Qa — условие установившегося движения.
Отношение толкаюшей силы Р к радиальной реакции Q называется коэффициентом сопротивления качению k.
На коэффициент сопротивления качению кроме шины значительное влияние оказывает качество дорожного покрытия.
Мощность Nк, затрачиваемая на качение ведомого колеса, равна произведению силы сопротивления качению Рс на линейную скорость качения V:
Раскрывая это уравнение, можно написать:
Nк = N1 + N2 + N3 — N4,
где N1 — мощность, затрачиваемая на деформацию шины;
N2 — мощность, затрачиваемая на проскальзывание шины в зоне контакта;
N3 — мощность, затрачиваемая на трение в подшипниках колеса и сопротивление воздуха;
N4— мощность, развиваемая шиной при восстановлении формы шины в момент выхода элементов из контакта.
Потери мощности на качение колеса значительно возрастают с увеличением скорости качения, так как в этом случае возрастает энергия деформации и, следовательно, большая часть энергии превращается в тепло.
При увеличении прогиба резко возрастает деформация каркаса и протектора шины, т. е. потери энергии на гистерезис.
Одновременно увеличивается теплообразование. Все это, в конечном итоге, ведет к увеличению мощности, затрачиваемой на качение шины.
Испытания показали, что на качение мотоциклетной шины в условиях ведомого колеса (по гладкому барабану) затрачивается мощность от 1,2 до 3 л. с. (в зависимости от размера шины и скорости качения).
Таким образом, общие потери от шин весьма значительны и соизмеримы с мощностью двигателя мотоцикла.
Совершенно очевидно, что решение вопроса снижения мощности, затрачиваемой на качение мотоциклетных шин, имеет исключительное значение. Уменьшение этих потерь не только увеличит долговечность шин, но значительно увеличит моторесурс двигателя и агрегатов мотоцикла, а также положительно скажется на топливной экономичности двигателей.
Исследования, проведенные при создании шин типа Р, показали, что потери мощности при качении шин этого типа значительно меньше (на 30—40%), чем у шин стандартной конструкции.
Кроме того, снижаются потери при переводе шин на двухслойный каркас из корда 232 КТ.
Особенно важно максимально снизить потери мощности при качении шин для гоночных мотоциклов, так как при их движении на высоких скоростях потери в шинах составляют до 30% по отношению к общим затратам мощности на движение. Один из методов снижения этих потерь — применение в каркасе гоночных шин капронового корда 0,40 К. Применив такой корд, уменьшили толщину каркаса, снизили вес шины, она стала более эластичной, менее подверженной нагреву.
Большое влияние на коэффициент сопротивления качению шины оказывает характер рисунка протектора.
Для уменьшения энергии, образующейся при входе элементов в контакт с дорогой, максимально снижена масса протектора гоночных шин. Если у дорожных шин глубина рисунка протектора находится в пределах 7—9 мм, то у гоночных шин она составляет 5 мм.
Кроме того, рисунок протектора гоночных шин выполняют таким образом, чтобы его элементы оказывали наименьшее сопротивление при качении шины.
Как правило, рисунок протектора шин переднего (ведомого) и заднего (ведущего) колес мотоцикла различен. Это объясняется тем, что назначение шины переднего колеса — обеспечение надежной управляемости, а заднего колеса — передача крутящего момента.
Наличие кольцевых выступов на шинах передних колес способствует снижению потерь при качении и улучшает управляемость и устойчивость, особенно на поворотах.
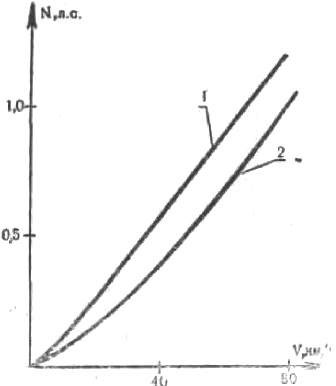
Рис. Кривые зависимости потерь мощности от скорости качения: 1 — шина размера 80-484 (3,25-19), модели Л-130 (дорожная); 2 — шина размера 85-484 (3,25-19) модели Л-179 (для заднего колеса шоссейно-кольцевых мотоциклов)
Зигзагообразный рисунок протектора заднего колеса обеспечивает надежную передачу крутящего момента и также снижает потери на качение. Все вышеизложенные меры позволяют в общем существенно снизить потери мощности при качении шин. На графике показаны кривые изменения потерь мощности при различных скоростях для дорожных и гоночных шин. Как видно из рисунка, гоночные шины по сравнению с дорожными имеют меньшие потери.
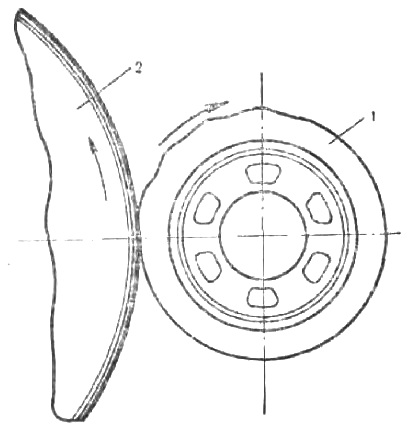
Рис. Появление «волны» при качении шины на критической скорости: 1 — шина; 2 — барабан испытательного стенда
Критическая скорость качения шины
Когда скорость качения шины достигает некоторого предельного значения, потери мощности на качение резко возрастают. Коэффициент сопротивления качению увеличивается примерно в 10 раз.
На поверхности беговой дорожки шины появляется «волна». Эта «волна», оставаясь неподвижной в пространстве, перемещается по каркасу шины со скоростью ее вращения.
Образование «волны» приводит к быстрому разрушению шины. В зоне протектора-каркаса резко увеличивается температура, так как внутреннее трение в шине становится более интенсивным, и уменьшается прочность связи между протектором и каркасом.
Под действием центробежных сил, значительных по величине при высоких скоростях качения, происходит отрыв участков протектора или элементов рисунка.
Скорость качения, при которой появляется «волна», считается критической скоростью качения шины.
Как правило, при качении на критической скорости шина разрушается после пробега 5—15 км.
При увеличении давления в шине критическая скорость увеличивается.
Однако практика показывает, что во время ШКХ скорость движения мотоциклов на некоторых участках на 20—25% превышает критическую скорость шин, определенную на стенде (при качении шины по барабану). При этом шины не разрушаются. Это объясняется тем, что при качении по плоскости деформация шины меньше (при одинаковом режиме), чем при качении по барабану, а следовательно, критическая скорость выше. Кроме того время движения мотоцикла со скоростью, превышающей критическую скорость шин, незначительно. При этом шина хорошо охлаждается встречным потоком воздуха. В связи с этим технические характеристики шин спортивных мотоциклов, предназначенных для ШКГ, допускают кратковременное превышение скорости в определенных пределах.
Качение шины в условиях ведущего и тормозного колеса. Качение шины в условиях ведущего колеса происходит при приложении к колесу крутящего момента Мкр.
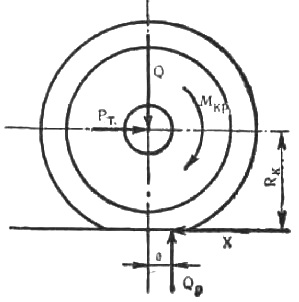
Схема сил, действующих на ведущее колесо, приведена на рисунке.
Рис. Схема сил, действующих на шину ведущего колеса при качении
К колесу, нагруженному вертикальной силой Q, приложен крутящий момент Мкр.
Реакция дороги Qp, равная по величине нагрузке Q, смещена относительно оси колеса на некоторое расстояние а. Сила Qp создает момент сопротивления качению Мс:
Крутящий момент Мкр создает тяговую ситу Рт:
где Rк— радиус качения.
При качении шины в условиях ведущего колеса под действием крутящего момента происходит перераспределение касательных сил в контакте.
В передней по направлению движения части контакта касательные силы увеличиваются, в задней — уменьшаются. При этом равнодействующая касательных сил X равна тяговой силе Рт.
Мощность, затрачиваемая на качение ведущего колеса, равна произведению крутящего момента Мкр на угловую скорость Wк вращения колеса:
Это уравнение справедливо только в том случае, когда в контакте отсутствует проскальзывание.
Однако касательные силы вызывают проскальзывание элементов рисунка протектора относительно дороги.
В силу этого действительная величина скорости поступательного движения колеса Уд несколько ниже теоретической Vт.
Отношение действительной скорости поступательного движения Vд к теоретической Vт называется коэффициентом полезного действия колеса, учитывающим потери скорости на проскальзывание шины относительно дороги.
Величину проскальзывания а можно оценить по следующей формуле:
Очевидно, значение действительной скорости Vд может меняться в пределах от Vт до 0, т. е.:
Интенсивность проскальзывания зависит от величины касательных сил, определяемых в свою очередь величиной крутящего момента.
Ранее было показано:
Mкр = XRк;
Х = Рт = Qv,
где v — коэффициент сцепления шины с дорогой.
При увеличении крутящего момента до некоторого значения, превышающего критическое, величина равнодействующей касательных сил X становится выше допустимой и шина полностью проскальзывает относительно дороги.
Cуществующие мотоциклетные шины в диапазоне рабочих нагрузок могут передавать без полного проскальзывания крутящий момент 55—75 кгс*м (в зависимости от размера шины, величины нагрузки, давления и т. д.).
При торможении мотоцикла силы, действующие на шину, по характеру аналогичны силам, возникающим при работе шины в условиях ведущего колеса.
При приложении к колесу тормозного момента Мт в зоне контакта происходит перераспределение касательных сил. Наибольшие касательные силы возникают в задней части контакта. Равнодействующая касательных сил по величине и направлению совпадает с тормозной силой Т:
При увеличении тормозного момента Мт выше некоторого критического значения тормозная сила Т становится больше силы сцепления шины с дорогой (T>Qv) и в контакте начинается полное проскальзывание, наступает явление юза.
При торможении на юз в зоне контакта повышается температура протектора, падает коэффициент сцепления, резко увеличивается износ рисунка протектора. Эффективность торможения уменьшается (увеличивается тормозной путь).
Наиболее эффективное торможение происходит при значениях тормозной силы Т, близкой по величине силе сцепления шины с дорогой.
Следовательно, при использовании водителем динамических качеств мотоцикла в целях уменьшения износа шин к ведущему колесу должен подводиться крутящий момент, обеспечивающий наименьшее проскальзывание шины относительно дороги.