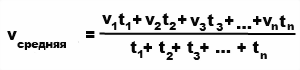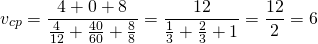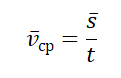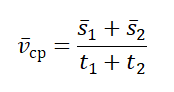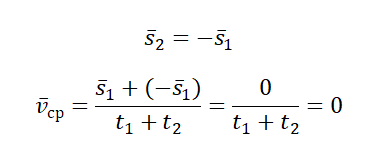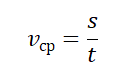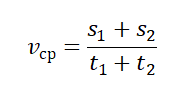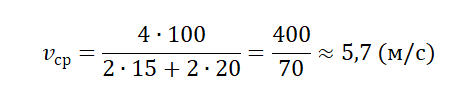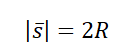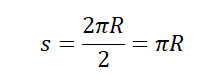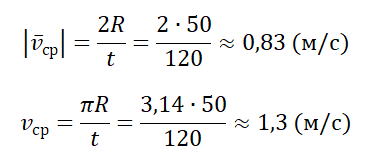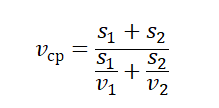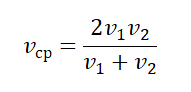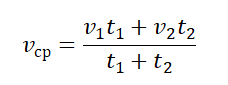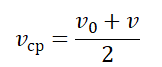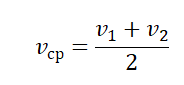Как находить среднюю скорость
Повторим, как находить среднюю скорость, и рассмотрим конкретные примеры.
Чтобы найти среднюю скорость, надо:
1) найти весь пройденный путь;
2) найти все время движения;
3) весь пройденный путь разделить на все время движения:
На примерах посмотрим, как находить среднюю скорость.
1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.
Находим весь пройденный путь: 2∙7 + 3∙5 = 29 км.
Находим все время движения: 2+3=5 часов.
Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.
2) Автомобиль проехал 2 часа по шоссе со скоростью 100 км/ч, 1,5 часа по грунтовой дороге со скоростью 40 км/ч и 30 минут по проселочной дороге со скоростью 26 км/ч. Найти среднюю скорость автомобиля на всем пути.
Переведем минуты в часы: 30 минут = 0,5 часа.
Найдем весь пройденный автомобилем путь:
2∙100 + 1,5∙40 + 0,5∙26 = 200 + 60 + 13= 273 км.
Находим все время движения:
Чтобы найти среднюю скорость движения автомобиля, разделим весь пройденный путь на все время движения:
3) Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.
Найдем весь путь велосипедиста:
3∙12 + 1∙0 + 2∙9 = 54 км.
Найдем все время движения:
Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:
195 Comments
самый лучший сайт по математике спасибо огромное
Илья, спасибо за теплые слова!
Велосипедист проехал со скоростью 12 км/ч 4 км,остановился на 40 мин и продолжил движение со скоростью 8 км/ч и проехал 8 км. Найдите скорость велосипедиста на протяжении всей дороги? Пожалуйста,помогите,очень важно
Валерий, эта задача — на движение по водному пути. Но ее можно решить логически.
Поскольку известно, что скорость катера по течению реки в два раза больше скорости против течения, при этом расстояние туда и обратно — одинаковое, то время, затраченное катером на путь по течению, в два раза меньше времени против течения (скорость и время — обратно пропорциональные величины. Если скорость увеличить в несколько раз, то при том же расстоянии время уменьшится во столько же раз).
Таким образом, все время можно разделить на 3 части, одну часть которого катер потратил на путь по течению, две — на путь против течения. Так как на весь путь было потрачено 2 часа=120 минут, то из них на путь по течению — 1/3 от 120 — это 40 минут=2/3 часа. Чтобы найти скорость, надо расстояние разделить на время: 20:(2/3)=30 км/ч — это скорость катера по течению. Она в два раза больше скорости против течения, следовательно, скорость против течения 30:2=15 км/ч.
Девушка ехала на работу со средней скоростью 40 миль в час, обратно домой ехала со средней скоростью 30 миль в час, весь путь от дома до работы и обратно занял 1 час, сколько миль проехала девушка?
Это — задача на движение. Пусть на работу девушка ехала х часов,тогда обратный путь занял у нее (1-х) часов. По формуле пути путь на работу равен 40х миль, обратный путь — 30(1-х) миль. Так как туда и обратно девушка проехала одинаковое расстояние, составляем уравнение: 40х=30(1-х). Отсюда х=3/7, путь на работу 40∙(3/7)=120/7 миль, туда и обратно — 2∙(120/7)=240/7=38 2/7 мили.
Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Текстовые задачи на среднюю скорость.
Чтобы найти среднюю скорость движения, необходимо все расстояние разделить на все время движения.
Задача 1. Первые 105 км автомобиль ехал со скоростью 35 км/ч, следующие 120 км – со скоростью 60 км/ч, а последние 500 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение:
Найдём время движения автомобиля:
1. 105:35=3(ч) — время, за которое автомобиль проехал 105 км со скоростью 35 км/ч.
2. 120:60=2(ч) — время, за которое автомобиль проехал 120 км со скоростью 60 км/ч.
3. 500:100=5(ч) — время, за которое автомобиль проехал 500 км со скоростью 100 км/ч.
4. 3+2+5=10(ч) — время движения автомобиля.
Найдём расстояние, которое проехал автомобиль:
Найдём среднюю скорость автомобиля:
Ответ: средняя скорость автомобиля равна 72,5 км/ч.
Задача 2. Первую половину трассы автомобиль проехал со скоростью 55 км/ч, а вторую – со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение:
Пусть автомобиль проехал Х км.
Найдём время движения автомобиля:
1. Х/110(ч) — время, за которое автомобиль проехал Х/2 км со скоростью 55 км/ч.
2. Х/140(ч) — время, за которое автомобиль проехал Х/2 км со скоростью 70 км/ч.
Найдем среднюю скорость:
Ответ: 61,6 км/ч.
Задачи для самостоятельного решения:
1. Первые 200 км автомобиль ехал со скоростью 50 км/ч, следующие 320 км – со скоростью 80 км/ч, а последние 140 км – со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
2. Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 180 км – со скоростью 60 км/ч, а последние 225 км – со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
3. Первую половину трассы автомобиль проехал со скоростью 65 км/ч, а вторую половину трассы со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Способы нахождения средней скорости в физике
Основные понятия и законы кинематики
Кинематика — раздел механики, описывающий механическое движение тел без рассмотрения причин, из-за которых происходит движение.
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Для описания движения нужна система отсчета, относительно которой мы будем описывать движение.
Система отсчета — это система координат, связанная с телом отсчета и прибор для измерения времени.
Тело отсчета — это тело, относительно которого рассматривают положение других тел.
Материальная точка — это тело, размеры которого можно не учитывать при решении задачи.
Траектория — это мысленная линия в пространстве, которую при движении описывает материальная точка.
Траектория движения делится на два типа:
Путь — это длина траектории, которую описывает тело или материальная точка за данный промежуток времени.
Перемещение S → — это вектор, соединяющий начальное положение тела или материальной точки с ее конечным положением.
Скорость — это векторная физическая величина, характеризующаяся направлением и быстротой перемещения материальной точки.
Определение средней скорости
Рассчитать среднюю скорость можно по следующей формуле:
Определение средней путевой скорости
Средняя путевая скорость — это отношение пути или длины траектории, пройденного телом, к интервалу времени, за которое этот путь был пройден.
Формула средней путевой скорости выглядит так:
Примеры решения задач
Автомобиль первый час ехал со скоростью 100 км/ч, после чего сделал остановку. Следующие два часа автомобиль ехал со скоростью 90 км/ч, а затем два часа — со скоростью 80 км/ч. Найдите среднюю скорость на протяжении всего пути автомобиля.
В условии сказано о трех участках пути.
ϑ с р → = S 1 → + S 2 → + S 3 → t 1 + t 2 + t 3
Участки пути мы можем вычислить и посчитать следующим образом:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
ϑ с р = 100 + 180 + 160 1 + 2 + 2 = 440 5 = 88 к м ч
Ответ: средняя скорость составляет 88 км/ч.
Автомобиль проехал по дороге расстояние 140 км за время, равное 2 часам, затем сделал остановку. После остановки автомобиль проехал 60 км за 3 часа. Какова средняя скорость автомобиля за весь путь?
ϑ с р → = ∆ S → ∆ t ϑ с р → = S 1 → + S 2 → t 1 + t 2 ϑ с р → = 140 + 60 2 + 3 = 40 к м ч
Ответ: средняя скорость автомобиля составляет 40 км/ч.
Человек занимается бегом и за 2 часа пробежал 5 км, а за следующий час пробежал 3 км. Определите среднюю скорость бегуна.
Искать среднюю скорость будем как во второй задаче.
Как найти среднюю скорость автомобиля после поездки в разных режимах?
Автор: Дмитрий Сапко
Для вычисления средней скорости поездки на современной машине достаточно подготовиться заранее, сбросив показатели суточного пробега на нуль, а также обнулив средние данные расхода и скорости. После этого вы сможете не засекать никакого времени, а также не продумывать формулы по расчету средней скорости поездки. Тем не менее, такой вариант не всегда подходит, да и не все автомобили оснащены хорошим бортовым компьютером. Потому следует разобраться с тем, как определять среднюю скорость и прочие параметры.
Находим среднюю скорость и средний расход поездки по факту
Если замеры средней скорости поездки важны для вас в коммерческих целях или в качестве отчетности для фирмы, в которой вы работаете, то проще всего купить GPS-навигатор, который обладает функцией учета скорости и времени, проведенного в дороге. Этот прибор полностью заменит бортовой компьютер и сможет без применения различных формул показать вам среднюю скорость поездки.
В иных случаях можно пользоваться более грубыми методами определения. Для замеров вам потребуется секундомер, который будет определять рабочее время поездки. То есть, для нас важна каждая секунда, которую автомобиль проводит в дороге. Время, проведенное на заправках или в придорожных кафе зачастую в расчет не входит. Задачи для точного замера следующие:
Предположим, на поездку у вас ушло ровно 5 часов, а пройденное по спидометру расстояние оказалось 300 километров. Это значит, что средняя скорость вашего автомобиля во время движения составила 60 км/ч. Если вы будете практиковать определение средней скорости для каждой дальней поездки, то будете удивлены низкими показателями.
Часто создается впечатление, что средняя скорость должна быть около 120 километров в час, но на деле оказывается меньше 60. Подобным образом вы сможете просчитать средний расход топлива. Нужно затраченные литры поделить на сотни километров пройденного расстояния. К примеру, если вы проехали 300 километров, то делать сумму литров нужно на 3.
Какой должна быть средняя скорость машины в поездке?
Многие задаются вопросом, а какой же на самом деле должна быть средняя скорость автомобиля. Просчитав удивительный факт того, что средняя скорость авто в трассовом режиме составила всего 80 километров в час, водитель начинает сомневаться в том, что он эффективно использует ресурс транспортного средства. На самом деле, такая скорость вполне допустима.
Оптимальной скоростью при движении по трассе является 90 км/ч, но далеко не всегда получает держать крейсерскую скорость постоянно. Иногда происходят ситуации, которые заставляют в течение нескольких минут ехать медленно. К примеру, можно тянуться за фурой, ожидая возможности обгона. Оптимальная средняя скорость на трассе будет зависеть от таких факторов:
Это лишь базовые факторы, которые влияют на среднюю скорость машины при трассовой поездке. На практике при отсутствии нарушений ПДД средняя скорость автомобиля на трассе составляет 75-80 километров в час. Достичь средней скорости в 90 км/ч можно только на определенном отрезке трассы. Потому не огорчайтесь, увидев небольшие значения на экране бортового компьютера.
Первым фактором, который нужно оценивать при выборе скоростного режима на трассе, является безопасность. Именно этот важный критерий иногда становится жертвой нехватки времени или желания показать достойные цифры средней скорости. На деле такие цели никогда не приводят к хорошим последствиям, потому всегда выбирайте безопасные режимы поездки.
Главным критерием выбора скоростного режима являются далеко не возможности машины, а ваши соображения о безопасности и уверенности поездки. Если вы считаете, что ехать со скоростью 90 км/ч при данных условиях опасно, то лучше выбрать более комфортный и уверенный режим. Тем не менее, существуют определенные рекомендации от производителей.
Первое, о чем стоит вспомнить в таком контексте разговора, является средний расход. Если вы будете поддерживать скорость машины на уровне 90 километров в час, то расход будет максимально близким к паспортным показателям расхода на трассе. Многие водители переживают по поводу того, что их машина на трассе расходует больше топлива, чем указано в документах. Происходит это по таким причинам:
Именно по этим причинам средние показатели расхода часто оказываются на порядок больше паспортных замеров. При определении расхода в трассовом режиме для технических характеристик машины производитель выполняет тестирование транспорта не треке, где машина едет с постоянной одной рекомендованной скоростью. Именно это позволяет достичь столь занимательных цифр расхода топлива.
Для получения максимальных выгод в расходе топлива и прочих характеристиках вашего автомобиля экспериментируйте и пробуйте разные режимы поездки. Не лишни будет и почитать отзывы о том, как люди эксплуатируют ваш тип транспорта. Это поможет максимально упростить эксплуатацию машины, сделать меньшим расход топлива и предсказать любые особенности поведения транспортного средства. Помните, что скорость должна быть оправданной. Предлагаем подборку видео ДТП, случившихся в частности из-за высокой скорости:
Подводим итоги
Если вы решили учитывать особенности вашей эксплуатации транспорта, следует начать с учета средней скорости при движении, а также средних показателей расхода. Если вы сможете учитывать эти показатели постоянно, вы также сможете улучшать средний расход, ведь в данном случае проснется спортивный интерес. Занимаетесь ли вы учетом средних показателей эксплуатации вашего авто?