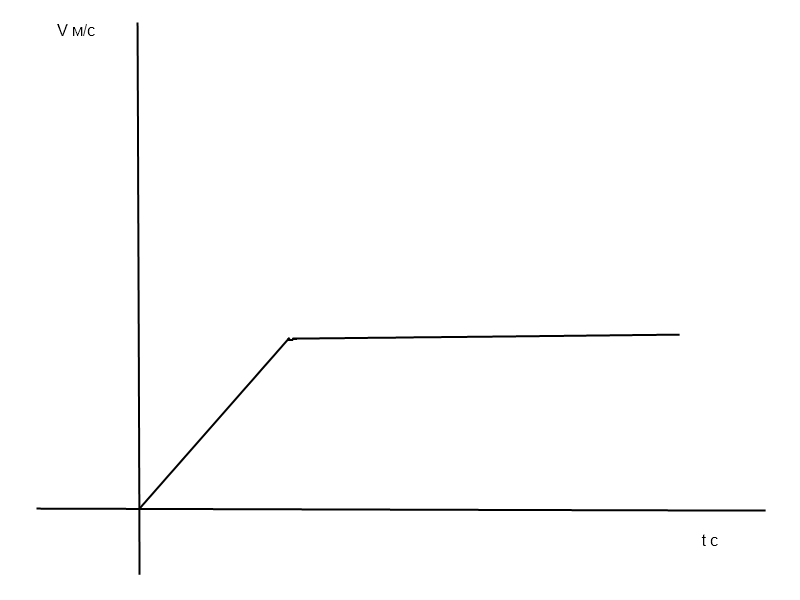
V = 30м/мин = 0,5 м/сек,
t = 2S/V = 2*0,18/0,5 = 0,72 сек
a = V/t = 0,5/0,72 = 25/36 = 0,7 м/с²
Проверка:
S = at²/2 = 0,7*0,72²/2 = 0,18 м
V = at = 0,7*0,72 = 0,5 м/с
1)
Находим период колебаний волны:
T = λ / V = 6/25 = 0,24 с
2)
Находим циклическую частоту:
ω = 2π / T = 2π / 0,24 ≈ 8,3·π с⁻1
3)
Перемещение частицы среды за период равно:
S = 0
5)
Максимальную скорость найдем из уравнения колебаний, взяв первую производную:
x(t) = Xmax*sin (ω*t+φ₀)
v(t) = x’ (t) = ω*Xmax*cos(ω*t+φ₀)
Vmax = ω*Xmax = 8,3·π·0,5 ≈ 8,3·3,14*0,5 ≈ 13 м/с
Запишем уравнение волны:
По условию:
Xmax/2 = Xmax*sin (φ₀)
1/2 = sin (φ₀)
φ₀ = π/6
Имеем:
x(t) = Xmax*sin (ω*t+φ₀) = 0,5*sin (8,3π*t + π/6)
1. Вещества в каком состоянии могут легко менять свою форму и объем?
В. В газообразном;
2. Автомобиль за 5 мин прошел путь 6км 600м. Какова скорость автомобиля?
Г. 22 м/с.
v = s/t = 6600 м/5*60 сек = 22 м/с
3. Каким явлением можно объяснить фразу: «Вода в реке становилась мутной»?
Не очень корректный вопрос. Если понимать диффузию, как смешивание, то диффузия.
А. Диффузией;
4. Мотоцикл «ИжП5» имеет массу 195кг. Каким станет его вес, если на него сядет человек массой 80кг?
Вес это сила, с которой давит на опору или растягивает нить подвеса тело. Тогда Р= (195+80)кг*10 м/c^2 = 2750 Н
В. 2750 Н;
5. Два человека несут бревно весом 800Н. С какой силой бревно давит на каждого их них?
На каждого из них по 800/2 = 400Н. Каждый из них давит на бревно по направлению вверх с силой 400 Н (реакция опоры) и сумма этих сил должны быть равна силе тяжести.
Б. 400Н;
6. При действии на опору силой 20 Н давление на нее оказывается в 200 Па. Во сколько раз изменится давление, если площадь опоры уменьшить в два раза?
Давление обратно пропорционально площади опоры. Уменьшение площади в 2 раза вызовет увеличение давления в 2 раза.
А. Увеличится в 2 раза;
7. При поднятии груза весом 140 Н с помощью подвижного блока на веревку действовали с силой 76 Н. Каков вес блока?
Г. 6 Н
8. Определите вес воды в бассейне размерами 25м х 4м х 2м. Плотность воды 1000 кг/м3.
Объем воды V = 25*4*2 = 200 м^3, тогда вес воды равен
Сначала равноускорено, потом равномерно.
На рисунке показано, как меняется с течением времени проекция вектора скорости тела?
На рисунке показано, как меняется с течением времени проекция вектора скорости тела.
Пользуясь графиком, определите проекцию \ ах \ и модуль |а| вектора ускорения, с которым движется это тело.
Автомобиль движется по прямой улице?
Автомобиль движется по прямой улице.
лена зависимость проекции скорости автомобиля от времени.
Определите проекцию максимального ускорения автомобиля.
Вопрос : на рисунке изображён график скорости равномерного движения?
Вопрос : на рисунке изображён график скорости равномерного движения.
Определите путь пройденный телом за 3 с.
Автомобиль движется по прямой улице?
Автомобиль движется по прямой улице.
На графике представлена проекция зависимости автомобиля от времени.
Определите проекцию максимального ускорения автомобиля.
Физика 10 скорость На рисунке приведен график зависимости проекции скорости некоторого тела от времени?
Физика 10 скорость На рисунке приведен график зависимости проекции скорости некоторого тела от времени.
Определите проекцию перемещения этого тела за 5с после начала движения.
СРОЧНО?
На рисунке представлен график зависимости проекции скорости движения тела от времени.
Добавить правильную зависимость проекции ускорения от времени, соответствующий этому движению.
На рисунке изображены графики зависимости проекции скорости тел от времени?
На рисунке изображены графики зависимости проекции скорости тел от времени.
Опишите движение тел.
Тело движется вдоль оси ОХ?
Тело движется вдоль оси ОХ.
На рисунке представлен график зависимости проекции скорости движения этого тела от времени.
Опишите движение тела (укажите скорость его движения в момент начала наблюдения, укажите направление и характер движения тела).
Определите ускорение движения тела.
Запишите уравнение зависимости проекции скорости и координаты тела от времени.
Тело движется вдоль оси ОХ?
Тело движется вдоль оси ОХ.
На рисунке представлен график зависимости проекции скорости движения этого тела от времени.
Опишите движение тела (укажите скорость его движения в момент начала наблюдения, укажите направление и характер движения тела).
Определите ускорение движения тела.
Запишите уравнение зависимости проекции скорости и координаты тела от времени.
ПОМОГИТЕ?
На рисунке изображен график зависимости проекции скорости гоночного автомобиля от времени.
Выполните задания, опираясь на данные рисунка.
А) Определите начальную скорость автомобиля и вычислите ускорение его движения.
Б) Опишите движение автомобиля.
В) Составьте уравнения зависимостей проекции скорости и координаты от времени, считая, что начальная координата равна 200 м.
Графики прямолинейного движения
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: \(\vec =0\).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: \(\vec =const\). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
Для каждого вида движения получим три графика. Графики будем называть так:
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой \(x_<0>\) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
\[x=x_<0>\]
Скорость и ускорение неподвижного тела равны нулю:
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка \(x_<0>\), а конечная координата — точка \(x\) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
Ускорение есть (рис. 4г) и оно не меняется:
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов \(\vec
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
Вычисление перемещения по графику проекции скорости
Из кодификатора по физике, 2020.
«1.1.3. Вычисление перемещения по графику зависимости υ(t).»
Теория
Пусть задан график зависимости проекции скорости от времени t (рис. 1).
Проекцию перемещения на ось 0Х будем считать:
— положительной, если проекция скорости на данную ось будет положительной (тело движется по направлению оси) (см. рис. 1);
— отрицательной, если проекция скорости на данную ось будет отрицательной (тело движется против оси) (рис. 2).
Путь s может быть только положительным:
Напоминаем формулы для расчета площадей фигур:
Задачи
Задача 1. По графику проекции скорости тела (рис. 3) определите проекцию его перемещения между 1 и 5 с.
где DC = Δt = 4 c, AD = 3 м/c, BC = 5 м/c. Тогда S = 16 м.
Проекция перемещения 0′ alt=’< s >_< x >>0′/>, т.к. проекция скорости 0′ alt=’< v >_< x >>0′/>.
м.
Задача 2. Автомобиль движется по прямой улице вдоль оси X. На рисунке 5 представлен график зависимости проекции скорости автомобиля от времени. Определите путь, пройденный автомобилем в течение указанных интервалов времени.
| Интервал времени | Путь |
| от 0 до 10 с | Ответ: м. |
| от 30 до 40 с | Ответ: м. |
В бланк ответов перенесите только числа, не разделяя их пробелом или другим знаком.
На интервале [0 с, 10 с] ищем площадь треугольника (рис. 6).
Путь равен значению площади (путь всегда положительный, т.е. s > 0).
На интервале [30 с, 40 с] ищем площадь трапеции (см. рис. 6).
где a = 10 м/c, b = 15 м/c, h = Δt = 40 c – 30 с = 10 с. Тогда м.
Задача 3. Определите за первые 4 с (рис. 7):
а) проекцию перемещения тела;
Ответ: а) ____ м; б) ____ м.
Так как при с проекция скорости поменяла знак, то получили две фигуры, два треугольника, площади которых равны:
, s = 45 м + 5 м = 50 м.
Задача 4. График зависимости проекции скорости материальной точки, движущейся вдоль оси 0Х, от времени изображен на рисунке 9. Определите перемещение точки, которое она совершила за первые 6 с.
Так как при и проекция скорости меняет знак, то получили три фигуры, три треугольника, площади которых равны:
Проекция перемещения 0′ alt=’< s >_< 1x >>0′/>, т.к. проекция скорости 0′ alt=’< v >_< 1x >>0′/>.