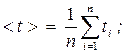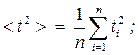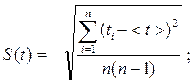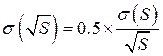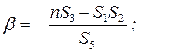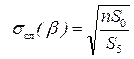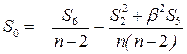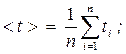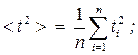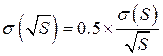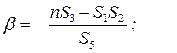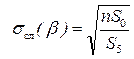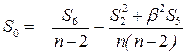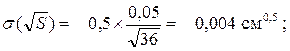Изучение прямолинейного движения с помощью машины атвуда

Лабораторная работа: Изучения прямолинейного движения на машине атвуда

Федеральное Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Лабораторная работа по курсу «Общая физика»

ИЗУЧЕНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ

Преподаватель Студент группы 220201

___________ /____________. / Стороженко Сергей Валерьевич

___________2011 г. 2011 г.

Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Название: Изучения прямолинейного движения на машине атвуда Раздел: Рефераты по физике Тип: лабораторная работа Добавлен 12:55:38 22 июня 2011 Похожие работы Просмотров: 3892 Комментариев: 18 Оценило: 5 человек Средний балл: 4.8 Оценка: неизвестно Скачать

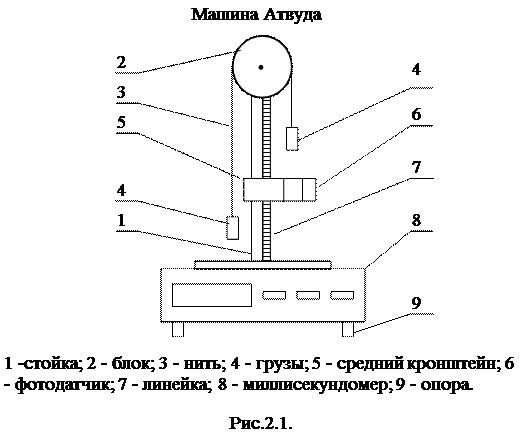Схема экспериментальной установки на основе машины Атвуда приведена на рис.2.1.

Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе.

Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Средние значения времени и квадрата времени 2 > прохождения грузом с перегрузом пути S:

Абсолютная суммарная погрешность измерения времени прохождения пути S:

(3.3)

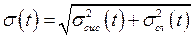
Абсолютная случайная погрешность измерения времени прохождения пути S:

стандартная абсолютная погрешность измерения времени:

Абсолютная суммарная погрешность косвенного измерения квадрата времени прохождения пути S:

Абсолютная погрешность косвенного измерения корня квадратного из расстояния:

Угловой коэффициент экспериментальной прямой:

b =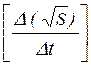 (3.8)

Величина ускорения, определяемого из линеаризованного графика:

Абсолютную случайную погрешность ускорения s_сл (a ) рассчитываем методом наименьших квадратов.

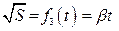
Рассчитываем параметры линеаризованного графика

(y = f(x) = Ax + B) и случайные абсолютные погрешности параметров.

Расчет производится по формулам: (3.10)

куда входят следующие величины:

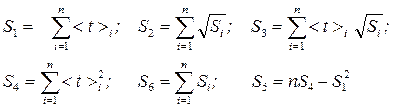
где n – число экспериментальных точек.

Абсолютная случайная погрешность определения углового коэффициента: s_сл (β ):

где вспомогательная величина:

Абсолютная случайная погрешность ускорения:

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.

Измеренные значения и результаты их обработки приведены в таблице 4.1.

Результаты прямых и косвенных измерений Таблица 4.1

=3,16 см 1/2

= 4,47 см 1/2

= 5,48 см 1/2

= 5,92 см 1/2

=6,48 см 1/2

Источник

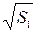
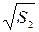
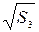
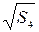
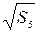
Лабораторная работа: Изучение прямолинейного движения тела на машине Атвуда

Федеральное Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Лабораторная работа по курсу «Общая физика»

ИЗУЧЕНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ

Преподаватель Студент группы 645-1

___________ /____________. / __________ / ____________ /

___________20__ г. __________ 20__ г.

Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Название: Изучение прямолинейного движения тела на машине Атвуда Раздел: Рефераты по физике Тип: лабораторная работа Добавлен 16:48:52 30 августа 2011 Похожие работы Просмотров: 113 Комментариев: 18 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать

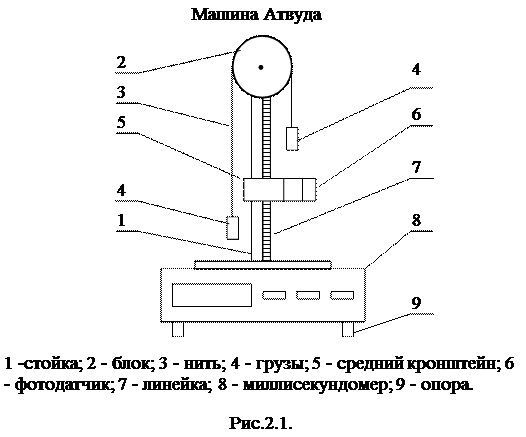Схема экспериментальной установки на основе машины Атвуда приведена на рис.2.1.

Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе.

Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Средние значения времени и квадрата времени 2 > прохождения грузом с перегрузом пути S:

Абсолютная суммарная погрешность измерения времени прохождения пути S:

(3.3)

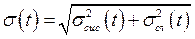
Абсолютная случайная погрешность измерения времени прохождения пути S:

Стандартная абсолютная погрешность измерения времени:

Абсолютная суммарная погрешность косвенного измерения квадрата времени прохождения пути S:

Абсолютная погрешность косвенного измерения корня квадратного из расстояния:

Угловой коэффициент экспериментальной прямой:

b =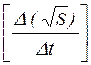 (3.8)

Величина ускорения, определяемого из линеаризованного графика:

Абсолютную случайную погрешность ускорения s_сл (a ) рассчитываем методом наименьших квадратов.

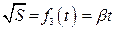
Рассчитываем параметры линеаризованного графика

(y = f(x) = Ax + B) и случайные абсолютные погрешности параметров.

Расчет производится по формулам: (3.10)

куда входят следующие величины:

где n – число экспериментальных точек.

Абсолютная случайная погрешность определения углового коэффициента: s_сл (β ):

где вспомогательная величина:

Абсолютная случайная погрешность ускорения:

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.

Измеренные значения и результаты их обработки приведены в таблице 4.1.

=

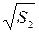
Средние значения времени и квадрата времени 2 > прохождения пути S, приведенные в таблице 4.1, рассчитаны по выражениям 3.1 и 3.2 (число точек измерения n=5 ).

Для первой точки измерения (S ₁ = 36 см):

Стандартную абсолютную погрешность измерения времени рассчитываем по формуле 3.5 для числа измерений n=5:

Δt₃ = t₃ − ₁ = 5,184−5,036 = 0,148 с; Δt₃ 2 = (0,148) 2 = 0,022 с 2 ;

Δt₄ = t₄ − ₁ = 5,066−5,036 = 0,030 с; Δt₄ 2 = (0,030) 2 = 0,001 с 2 ;

Δt₅ = t₅ − ₁ = 5,084−5,036 = 0,048 с; Δt₅ 2 = (0,048) 2 = 0,002 с 2 ;

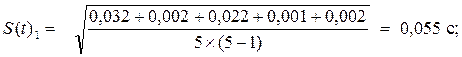
Абсолютная случайная погрешность измерения времени прохождения пути определяется по формуле 3.4. При доверительной вероятности a=0,9 и числе измерений n =5 коэффициент Стьюдента t(a, n ) = 2,1:

Результаты расчетов погрешностей

прямых и косвенных измерений времени и квадрата времени.

Абсолютную систематическую приборную погрешность измерения времени определяем как половину цены наименьшего деления секундомера :

Абсолютная суммарная погрешность измерения времени прохождения пути по формуле 3.3 :

Так как величина σ_сис (t) много меньше величины σ_сл (t )₁ (σ_сис (t) = 0,0005 с 2 )₁ = 2×5,036×0,116 = 1,168 с 2 ;

Результаты измерений записываем в виде ± σ(t) :

Результаты расчетов случайной, приборной и общей погрешности измерений времени и квадрата времени приведены в таблице 4.2.

Абсолютную погрешность измерения расстояния определяем как половину цены деления линейки:

Абсолютная погрешность косвенного измерения корня квадратного из расстояния по формуле 3.7 :

Для остальных точек измерений (при других значениях S) расчет проводится аналогично.

Результаты расчетов приведены в таблицах 4.2 и 4.3.

, см 0,5

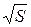
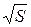
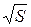
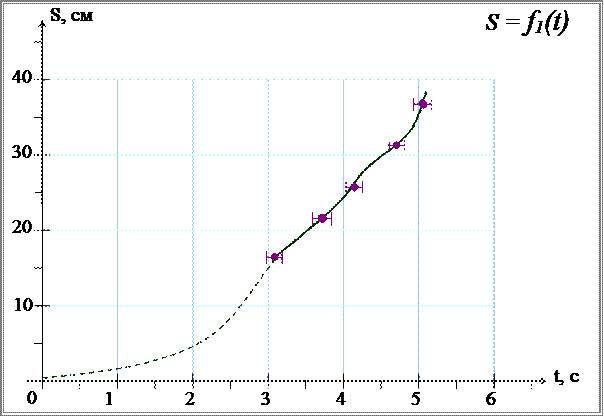
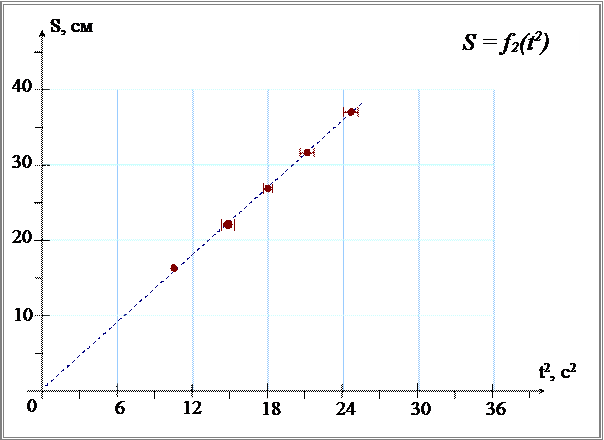
σ(). см 0,5

( )× , c× см 0,5

На основании данных, приведенных в таблицах 4.2, 4.3 строим графики зависимостей S = f ₁ ( t ) ( рис. 4.1.) и S = f ₂ ( t 2 ) ( рис. 4.2.), на графиках наносим доверительные интервалы.

Рисунок 4.1. Зависимость пройденного пути S от времени t .

Рисунок 4.2. Зависимость пройденного пути S от квадрата времени t 2 .

Рисунок 4.3. Зависимость 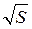от времени t .

На графике (рис. 4.3) видно, что прямая пересекает доверительные интервалы для всех экспериментальных точек.

Определим из графика угловой коэффициент прямой по формуле 3.8:

Величину ускорения определим по формуле 3.9:

По методу наименьших квадратов (МНК) рассчитаем параметр b линеаризованного графика 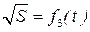= b t и случайную абсолютную погрешность параметра s_сл (b ).

По формулам 3.11, используя данные таблицы 4.3, определяем значение величин S ₁ − S ₆ для расчета по МНК (число точек n =5):

По формуле 3.10 определим параметр b линеаризованного графика:

b = (5×108,6 − 21,08 ×25,25) / 9,4 = 1,14 см 1/2 /c.

Угловой коэффициент прямой b = 1,14 см 1/2 /c.

Значение вспомогательной величины S ₀ по формуле 3.13:

S ₀ = 130/ 3 – (25,25 2 + 1,14 2 ×9,4 ) / 15 = 0,01 см.

По формуле 3.12 определим погрешность вычисления углового коэффициента прямой:

Величина ускорения по формуле 3.9 :

Абсолютная случайная погрешность ускорения по формуле 3.14 :

В результате проделанной работы мы смогли в пределах погрешностей измерений построить линеаризованный график зависимости 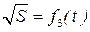. Все точки в этой зависимости укладываются на прямую в пределах их погрешностей.

Подтвердили справедливость закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда:

где S – путь пройденный телом за время движения t,

a – ускорение движения.

В ходе работы определена величина ускорения и сделана оценка ее погрешности:

6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ

6.1.Какие силы действуют на груз с перегрузом во время движения? Сила тяжести и сила натяжения нити.

6.4.Каким образом из линеаризованного графика можно оценить систематическую погрешность измерения времени. Систематическая погрешность приводит к тому, что прямая не будет проходить из начала координат. Величина отклонения от начала координат – систематическая погрешность.
6.5. Укажите физические допущения, используемые при теоретическом анализе движения грузов.
Блок и нить невесомы, нить нерастяжима, сила трения отсутствует.

Источник

Изучение прямолинейного движения на машине Атвуда

Автор работы: Пользователь скрыл имя, 05 Ноября 2011 в 12:29, лабораторная работа

Краткое описание

Целью работы является изучение основных законов динамики поступательного и вращательного движений тел, экспериментальное определение момента инерции блока и сравнение его с расчетным значением.

Отчет по ЛР№1.doc

Федеральное Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Лабораторная работа по курсу «Общая физика»

ИЗУЧЕНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ

Преподаватель Студент группы

___________2009 г. 2009 г.

Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Схема экспериментальной установки на основе машины Атвуда приведена на рис.2.1.

Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе.

Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Средние значения времени и квадрата времени 2 > прохождения грузом с перегрузом пути S:

Абсолютная суммарная погрешность измерения времени прохождения пути S:

Абсолютная случайная погрешность измерения времени прохождения пути S:

стандартная абсолютная погрешность измерения времени:

Абсолютная суммарная погрешность косвенного измерения квадрата времени прохождения пути S:

Абсолютная погрешность косвенного измерения корня квадратного из расстояния:

Угловой коэффициент экспериментальной прямой:

Величина ускорения, определяемого из линеаризованного графика:

Абсолютную случайную погрешность ускорения s _сл(a) рассчитываем методом наименьших квадратов.

Рассчитываем параметры линеаризованного графика

(y = f(x) = Ax + B) и случайные абсолютные погрешности параметров.

Расчет производится по формулам: (3.10)

куда входят следующие величины:

где n – число экспериментальных точек.

Абсолютная случайная погрешность определения углового коэффициента: s _сл( β ):

где вспомогательная величина:

Абсолютная случайная погрешность ускорения:

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.

Измеренные значения и результаты их обработки приведены в таблице 4.1.

Результаты прямых и косвенных измерений Таблица 4.1

Средние значения времени и квадрата времени 2 > прохождения пути S, приведенные в таблице 4.1, рассчитаны по выражениям 3.1 и 3.2 (число точек измерения n=5 ).

Для первой точки измерения (S₁ = 7 см):

Стандартную абсолютную погрешность измерения времени рассчитываем по формуле 3.5 для числа измерений n=5:

Δt₂= t₂ − ₁ = 2,603 − 2,450 = 0,153 с; Δt₁ 2 = (0,153) 2 = 0,023409 с 2 ;

Δt₄= t₄ − ₁ = 2,562 − 2,450 = 0,112 с; Δt₁ 2 = (0,112) 2 = 0,012544 с 2 ;

Результаты расчетов погрешностей

прямых и косвенных измерений времени и квадрата времени.

Источник

Исследование прямолинейного движения тел на машине Атвуда (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2

ГЛАВА II. МЕХАНИКА МАТЕРИАЛЬНОЙ ТОЧКИ

Лабораторная работа №1

ИССЛЕДОВАНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ
НА МАШИНЕ АТВУДА

Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Предварительно изучите теоретические основы работы №8.

Механическим движением называется происходящее со временем перемещение тел или их частей относительно других тел (тел отсчета). Любое механическое движение рассматривается в определенной системе отсчета, состоящей из тела отсчета, связанной с ним системы пространственных координат и часов.

, (1)

называют основным уравнением динамики.

, (2)

а для другого груза:

. (3)

Основное уравнение динамики вращательного движения неподвижного блока имеет вид:

, (4)

Если вращение по часовой стрелке считать положительным, то, согласно рис.2, получим

, (4¢)

Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:

, т. е. ; . (5)

Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:

. (6)

Наконец, в отсутствие скольжения нити по блоку ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:

или . (7)

Проецируя уравнения (2) и (3) на ось У, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4¢):

(8)

. (9)

В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство

6. Устранив возможные колебания грузов, нажмите кнопку «ПУСК» до ее фиксирования.

7. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло «ВРЕМЯ, С».

8. Нажмите кнопку «СБРОС».

9. Повторите пункты 2¸8 не менее четырех раз, меняя расстояние L2 между средним и нижним кронштейнами.

Если формула справедлива, то экспериментальные точки лежат на прямой, тангенс угла наклона которой определяет величину ускорения а грузов с перегрузком.

11. Найдите величину ускорения а по методу наименьших квадратов:

; ;

;

; ,

где — коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы .

Результат измерения а: а ± D а.

Используя найденные значения а и с, постройте на графике с экспериментальными точками прямую линию у = ах + с.

Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ
СВОБОДНОГО ПАДЕНИЯ

12. Определите величину ускорения свободного падения g по формуле

.

Полуширину доверительного интервала Dg найдите с помощью формулы:

.

2. Что называется системой отсчета?

3. Дайте определение материальной точки.

4. Сравните понятия пути и перемещения.

5. Дайте определения средней и мгновенной скоростей.

6. Дайте определения среднего и мгновенного ускорений.

7. Как зависит траектория движения от направления ускорения?

8. Укажите формулы, связывающие кинематические величины при равноускоренном прямолинейном движении.

9. Дайте определение силы.

10. Что характеризует масса тела?

12. Какая система тел называется изолированной?

13. Сформулируйте законы сохранения импульса и механической энергии.

14. Какое движение тела называется свободным падением?

15. Как записать 2-ой закон Ньютона для свободного падения?

16. Как ускорение свободного падения зависит от широты точки наблюдения?

17. Почему величина ускорения свободного падения на уровне моря различна на полюсе и экваторе?

18. Как уменьшится ускорение свободного падения при подъеме с уровня моря на высоту h = 10 км? Радиус Земли R3=6370 км.

19. Нарисуйте эскиз машины Атвуда.

20. При каком условии ускорения тел, используемых в машине Атвуда, одинаковы по модулю?

21. При каких условиях одинаковы силы натяжения нитей по обе стороны неподвижного блока?

22. Как движется система тел в машине Атвуда?

23. Какое время измеряет секундомер машины Атвуда?

24. Укажите зависимость квадрата скорости равноускоренного движения системы тел от величины перемещения.

25. Какие величины определяют с помощью прямых измерений в данной лабораторной работе?

26. Какие сделаны допущения при выводе формулы ускорения системы тел?

27. По какой формуле определяют величину ускорения свободного падения g?

28. Найдите ускорение свободного падения, если масса
перегрузка в 4 раза меньше массы одного груза, а ускорение системы грузов с перегрузком равно а = 1,1 м/с2.

29. По какой формуле можно найти полуширину доверительного интервала Dg ускорения свободного падения?

30. Можно ли использовать закон сохранения механической энергии для описания движения системы тел в машине Атвуда?

Лабораторная работа №2

ИЗУЧЕНИЕ АБСОЛЮТНО НЕУПРУГОГО УДАРА
НА МОДЕЛИ КОПРА

Изучение абсолютно неупругого удара. Оценка действующих сил и величины необратимых потерь механической энергии при абсолютно неупругом ударе.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Материальной точкой называется тело, размеры которого много меньше масштаба движения. В дальнейшем в этом пункте под словом «тело» следует подразумевать материальную точку.

Силы, действующие на тела механической системы, можно разделить на две группы:

1) внешние силы , с которыми на тело с номером i действуют тела, не вошедшие в систему;

2) внутренние силы взаимодействия тел системы с номерами i и k. По третьему закону Ньютона :

или . (1)

Система тел называется изолированной или замкнутой, если на тела системы не действуют внешние силы, т. е. .

Если ускорение записать в виде ,
где — малое изменение скорости тела за малый промежуток времени Dt, то второй закон Ньютона принимает вид

или , (2)

где — начальная скорость тела; — конечная скорость спустя малый промежуток времени Dt. Величина — импульс тела, а — импульс силы.

Рассмотрим систему двух тел с массами m1 и m2. Пусть тела системы взаимодействуют с силами и и на тела действуют внешние силы и . Запишем уравнение (2) для каждого тела системы:

; (3)

. (4)

Складывая уравнения (3) и (4) и учитывая равенство (1), получим

. (5)

Из уравнения (5) следует закон сохранения импульса: если система является изолированной (;), то суммарный импульс тел такой системы сохраняется, т. е.

. (6)

Изменение скорости соударяющихся тел может быть достаточно большим, а время удара Dt очень мало (с). Поэтому ускорения тел и внутренние или ударные силы во время удара могут быть очень большими. Эти силы значительно превосходят внешние силы: . Мерой механического воздействия на тело за время удара является импульс ударной силы :

,

где — средняя ударная сила за время Dt.

Импульсами внешних сил, например, сил тяжести, а также перемещениями тел за малое время удара Dt можно пренебречь. В этом случае уравнения (3) и (4) принимают вид:

; (3¢)

. (4¢)

Складывая уравнения (3¢) и (4¢) с учетом (1), получим уравнение (6), т. е. при кратковременных взаимодействиях даже в неизолированных системах закон сохранения импульса приближенно выполняется.

Удар называется абсолютно неупругим, если после удара скорости тел одинаковы: . Для такого удара уравнение (6) принимает вид

.

Изменение кинетической энергии тел при абсолютно неупругом ударе равно

. (7)

Для кратковременного удара изменениями положения тел и их потенциальной энергии Ер можно пренебречь: DЕр = 0.

Полуширина доверит. инт.
Dх

Результаты вычислений занесите в таблицу 1. Сравните силу трения F для разных значений L длины рычага, т. е. для разных величин силы нормального давления.

Источник