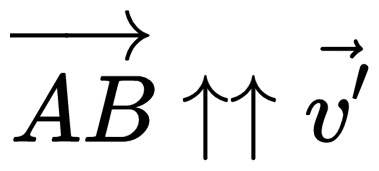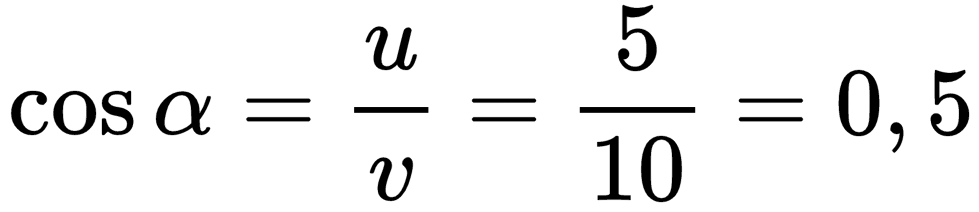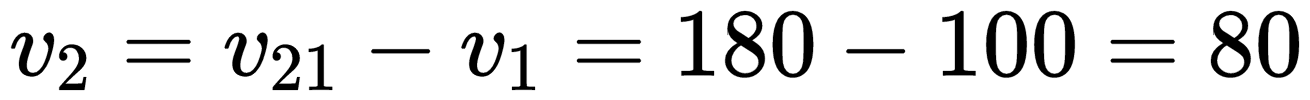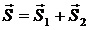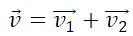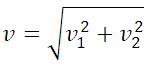§ 9. Относительность движения
В курсе физики 7 класса упоминалось об относительности механического движения. Рассмотрим этот вопрос более подробно на примерах и сформулируем, в чём конкретно заключается относительность движения.
Человек идёт по вагону против движения поезда (рис. 16). Скорость поезда относительно поверхности земли равна 20 м/с, а скорость человека относительно вагона равна 1 м/с. Определим, с какой скоростью и в каком направлении движется человек относительно поверхности земли.
Будем рассуждать так. Если бы человек не шёл по вагону, то за 1 с он переместился бы вместе с поездом на расстояние, равное 20 м. Но за это же время он прошёл расстояние, равное 1 м, против хода поезда. Поэтому за время, равное 1 с, он сместился относительно поверхности земли только на 19 м в направлении движения поезда. Значит, скорость человека относительно поверхности земли равна 19 м/с и направлена в ту же сторону, что и скорость поезда. Таким образом, в системе отсчёта, связанной с поездом, человек движется со скоростью 1 м/с, а в системе отсчёта, связанной с каким-либо телом на поверхности земли, — со скоростью 19 м/с, причём направлены эти скорости в противоположные стороны. Отсюда следует, что скорость относительна, т. е. скорость одного и того же тела в разных системах отсчёта может быть различной как по числовому значению, так и по направлению.
Теперь обратимся к другому примеру. Представьте вертолёт, вертикально опускающийся на землю. Относительно вертолёта любая точка винта, например точка А (рис. 17), будет всё время двигаться по окружности, которая на рисунке изображена сплошной линией. Для наблюдателя, находящегося на земле, та же самая точка будет двигаться по винтовой траектории (штриховая линия). Из этого примера ясно, что траектория движения тоже относительна, т. е. траектория движения одного и того же тела может быть различной в разных системах отсчёта.
Следовательно, путь является величиной относительной, так как он равен сумме длин всех участков траектории, пройденных телом за рассматриваемый промежуток времени. Это особенно наглядно проявляется в тех случаях, когда физическое тело движется в одной системе отсчёта и покоится в другой. Например, человек, сидящий в движущемся поезде, проходит определённый путь s в системе, связанной с землёй, а в системе отсчёта, связанной с поездом, его путь равен нулю.
Таким образом, относительность движения проявляется в том, что скорость, траектория, путь и некоторые другие характеристики движения относительны, т. е. они могут быть различны в разных системах отсчёта.
Понимание того, что движение одного и того же тела можно рассматривать в разных системах отсчёта, сыграло огромную роль в развитии взглядов на строение Вселенной.
С давних пор люди замечали, что звёзды в течение ночи, так же как и Солнце днём, перемещаются по небу с востока на запад, двигаясь по дугам и делая за сутки полный оборот вокруг Земли. Поэтому в течение многих столетий считалось, что в центре мира находится неподвижная Земля, а вокруг неё обращаются все небесные тела. Такая система мира была названа геоцентрической (греческое слово «гео» означает «земля»).
Во II в. александрийский учёный Клавдий Птолемей обобщил имеющиеся сведения о движении светил и планет в геоцентрической системе и сумел составить довольно точные таблицы, позволяющие определять положение небесных тел в прошлом и будущем, предсказывать наступление затмений и т. д.
Однако со временем, когда точность астрономических наблюдений возросла, стали обнаруживаться расхождения между вычисленными и наблюдаемыми положениями планет. Вносимые при этом исправления делали теорию Птолемея очень сложной и запутанной. Появилась необходимость замены геоцентрической системы мира.
Новые взгляды на строение Вселенной были подробно изложены в XVI в. польским учёным Николаем Коперником. Он считал, что Земля и другие планеты движутся вокруг Солнца, одновременно вращаясь вокруг своих осей. Такая система мира называется гелиоцентрической, поскольку в ней за центр Вселенной принимается Солнце (по-гречески «гелиос»).
Таким образом, в гелиоцентрической системе отсчёта движение небесных тел рассматривается относительно Солнца, а в геоцентрической — относительно Земли.
Как же с помощью системы мира Коперника можно объяснить видимое нами суточное обращение Солнца вокруг Земли? На рисунке 18 схематично изображён земной шар, освещаемый с одной стороны солнечными лучами, и человек (наблюдатель), который в течение суток находится в одном и том же месте Земли. Вращаясь вместе с Землёй, он наблюдает за перемещением светил.
Воображаемая ось, вокруг которой вращается Земля, как бы пронзает земной шар, проходя через Северный (N) и Южный (S) географические полюсы. Стрелочка указывает направление вращения Земли — с запада на восток.
1 Скорость вращения точек поверхности Земли относительно оси зависит от широты местности: она возрастает от нуля (на полюсах) до 465 м/с (на экваторе).
Итак, по системе мира Коперника видимое вращение Солнца и звёзд, т. е. смена дня и ночи, объясняется вращением Земли вокруг своей оси. Время, за которое земной шар делает полный оборот, называется сутками.
Гелиоцентрическая система мира оказалась гораздо более удачной, чем геоцентрическая, при решении многих научных и практических задач.
Таким образом, применение знаний об относительности движения позволило по-новому взглянуть на строение Вселенной. А это, в свою очередь, помогло впоследствии открыть физические законы, описывающие движение тел в Солнечной системе и объясняющие причины такого движения.
Вопросы
1. В чём проявляется относительность движения? Ответ проиллюстрируйте примерами.
2. В чём основное отличие гелиоцентрической системы мира от геоцентрической?
3. Объясните смену дня и ночи на Земле в гелиоцентрической системе (см. рис. 18).
Упражнение 9
1. Вода в реке движется со скоростью 2 м/с относительно берега. По реке плывёт плот. Какова скорость плота относительно берега; относительно воды в реке?
2. В некоторых случаях скорость тела может быть одинаковой в разных системах отсчёта. Например, поезд движется с одной и той же скоростью в системе отсчёта, связанной со зданием вокзала, и в системе отсчёта, связанной с растущим у дороги деревом. Не противоречит ли это утверждению о том, что скорость относительна? Ответ поясните.
3. При каком условии скорость движущегося тела будет одинакова относительно двух систем отсчёта?
4. Благодаря суточному вращению Земли человек, сидящий на стуле в своём доме в Москве, движется относительно земной оси со скоростью примерно 900 км/ч. Сравните эту скорость с начальной скоростью пули относительно пистолета, которая равна 250 м/с.
5*. Торпедный катер идёт вдоль шестидесятой параллели южной широты со скоростью 90 км/ч по отношению к суше. Скорость суточного вращения Земли на этой широте равна 223 м/с. Чему равна (в СИ) и куда направлена скорость катера относительно земной оси, если он движется на восток; на запад?
Относительность механического движения
теория по физике 🧲 кинематика
Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.
Относительность перемещения
Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.
Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.
Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:
Относительность скорости в ПСО и НСО
Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.
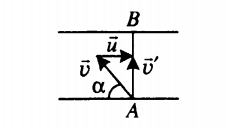
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.
Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:
Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):
Косинусу 0,5 соответствует угол, равный 60 градусам.
Относительная скорость двух тел
Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.
Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:
v отн — относительная скорость, или скорость первого тела относительно второго, v 1 и v 2 — скорость первого и второго тела относительно СО.
Варианты обозначения относительной скорости и их проекций:
Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.
Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.
Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:
Скорость второго автомобиля относительно дороги равна 80 км/час.
Правила сложения векторов
| Сложение двух сонаправленных векторов | |
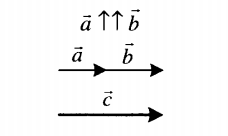 | Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b. |
| Сложение двух противоположно направленных векторов | |
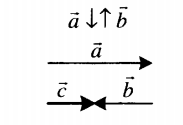 | Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|. |
| Сложение двух векторов, расположенных друг к другу под углом | |
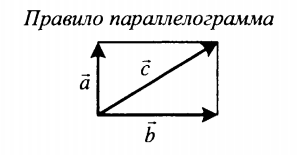
| Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
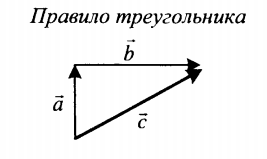 | Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: 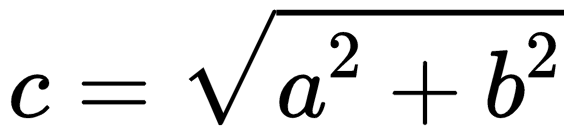 . . |
 | |
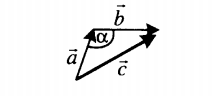 | Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: 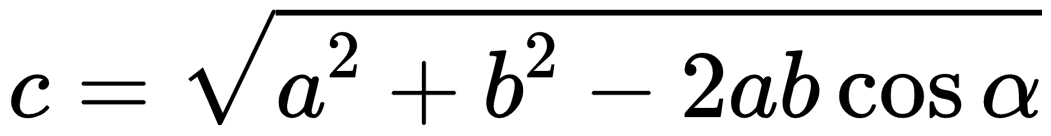 . . |
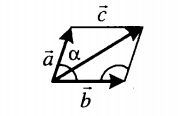 | Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: 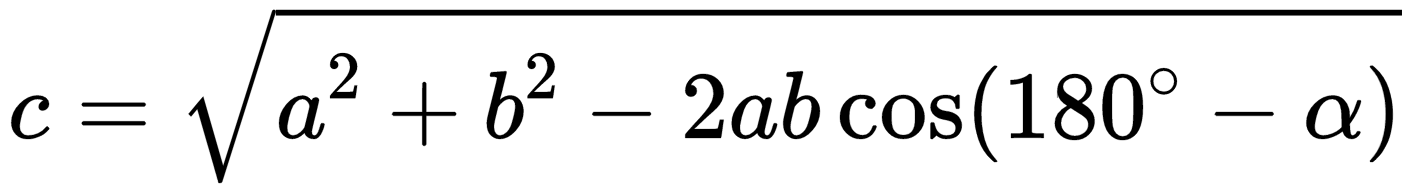 . . |
Правила вычитания векторов
Эта таблица иллюстрирует правила вычитания векторов на примере векторов 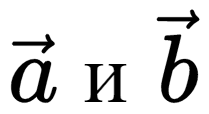
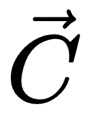
Алгоритм решения
Решение
Записываем данные относительно Земли:
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость второго автомобиля относительно оси ОХ ( v 2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v 1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость автомобиля относительно земли ( v 1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v 2). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
pазбирался: Алиса Никитина | обсудить разбор | оценить
Как сказал.
Информация в чистом виде ‒ это не знание. Настоящий источник знания ‒ это опыт.
Альберт Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля

Я учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Урок 02. (дополнительный материал). Относительность механического движения
Относительность механического движения.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным.
Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляетсяотносительность механического движения.
Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Покой тоже относителен. Например, пассажир в покоящемся поезде смотрит на проходящий мимо поезд и не понимает, какой поезд движется, пока не посмотрит на небо или землю.
Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое. По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.
Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.
Движение одного и того же тела может выглядеть по-разному с точки зрения различных наблюдателей. Скорость, направление движения и вид траектории тела будут различными для различных наблюдателей. Без указания тела отсчета разговор о движении является бессмысленным. Например, сидящий пассажир в поезде покоится относительно вагона, но движется вместе с вагоном относительно платформы вокзала.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.
Галилей показал, что в условиях Земли практически справедлив закон инерции. Согласно этому закону действие на тело сил проявляется в изменениях скорости; для поддержания же движения с неизменной по величине и направлению скоростью не требуется присутствия сил. Системы отсчета, в которых выполняется закон инерции, стали называть инерциальные системы отсчета (ИСО).
Системы, которые вращаются или ускоряются, неинерциальные.
Землю нельзя считать вполне ИСО: она вращается, но для большинства наших целей системы отсчета, связанные с Землей, в достаточно хорошем приближении можно принять за инерциальные. Система отсчета, движущаяся равномерно и прямолинейно относительно ИСО, также инерциальная.
Г. Галилей и И. Ньютон глубоко осознавали то, что мы сегодня называем принципом относительности, согласно которому механические законы физики должны быть одинаковыми во всех ИСО при одинаковых начальных условиях.
Из этого следует: ни одна ИСО ничем не отличается от другой системы отсчета. Все ИСО эквивалентны с точки зрения механических явлений.
Принцип относительности Галилея исходит из некоторых допущений, которые опираются на наш повседневный опыт. В классической механике пространство и время считаются абсолютными. Предполагается, что длина тел одинакова в любой системе отсчета и что время в различных системах отсчета течет одинаково. Предполагается, что масса тела, а также все силы остаются неизменными при переходе из одной ИСО в другую.
В справедливости принципа относительности нас убеждает повседневный опыт, например в равномерно движущемся поезде или самолете тела движутся так же, как и на Земле.
Не существует эксперимента, с помощью которого можно было бы установить, какая система отсчета действительно покоится, а какая движется. Нет систем отсчета в состоянии абсолютного покоя.
Если на движущейся тележке подбросить монету вертикально вверх, то в системе отсчета, связанной с тележкой, будет изменяться только координата ОУ.
В системе отсчета, связанной с Землей, изменяются координаты ОУ и ОХ.
Следовательно, положение тел и их скорости в разных системах отсчета различны.
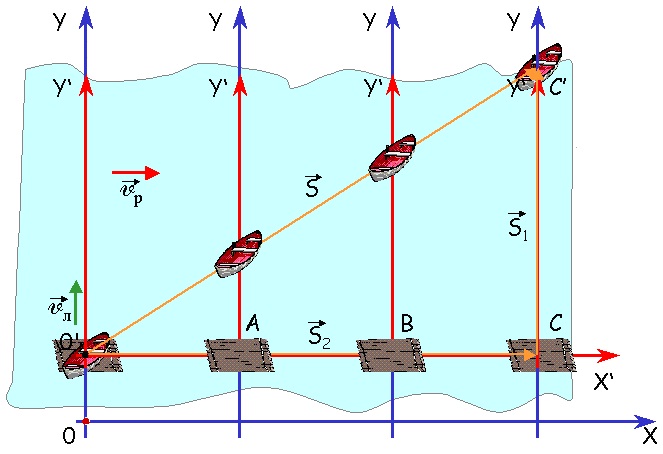
Рассмотрим движение одного и того же тела относительно двух разных систем отсчета: неподвижной и движущейся.
Лодка пересекает реку перпендикулярно течению реки двигаясь с некоторой скоростью относительно воды. За движением лодки следят 2 наблюдателя: один неподвижный на берегу, другой на плоту, плывущем по течению. Относительно воды плот неподвижен, а по отношению к берегу он движется со скоростью течения.
С каждым наблюдателем свяжем систему координат.
X0Y – неподвижная система координат.
X’0’Y’ – подвижная система координат.
S – перемещение лодки относительно неподвижной СО.
S1 – перемещение лодки относительно подвижной СО
S2 – перемещение подвижной системы отсчета относительно неподвижной СО.
По закону сложения векторов
Скорость получим разделив S на t:
v – скорость тела относительно неподвижной СО
v1 – скорость тела относительно подвижной СО
v2 – скорость подвижной системы отсчета относительно неподвижной СО
Эта формула выражает классический закон сложения скоростей: скорость тела относительно неподвижной СО равна геометрической сумме скорости тела относительно подвижной СО и скорости подвижной СО относительно неподвижной СО.
В скалярном виде формула будет иметь вид:
Впервые эту формулу получил Галилей.
Принцип относительности Галилея: все инерциальные системы отсчета равноправны; ход времени, масса, ускорение и сила в них записываются одинаково.
Скачать презентацию с Яндекса
Изобразите линейку ускорений с которыми могут двигаться различные автомобили
1. В чем состоит относительность положения тела?
Положение тела (его координаты) относительно, т.к. координаты тела могут быть различны в разных системах отсчета.
Например:
— автомобиль стоит в 20 метрах относительно остановки автобуса,
— этот же автомобиль находится в 10 метрах от ближайшего дома.
2. В чём проявляется относительность движения?
Относительность движения проявляется в том, что скорость, траектория, путь и некоторые другие характеристики движения относительны, т. е. они могут быть различны в разных системах отсчёта.
а) Скорость относительна, т. е. скорость одного и того же тела в разных системах отсчёта может быть различной как по числовому значению, так и по направлению.
б) Траектория движения относительна, т. е. траектория движения одного и того же тела может быть различной в разных системах отсчёта.
в) Путь является величиной относительной, так как он равен сумме длин всех участков траектории, пройденных телом за рассматриваемый промежуток времени.
Например:
Летчик в летящем самолете за время полета самолета:
в системе отсчета, связанной с какой-либо точкой на земле, преодолевает огромный путь,
в системе отсчета, связанной с самолетом, летчик находится в состоянии покоя и его путь, пройденный относительно самолета, равен нулю.
3. В чём основное отличие гелиоцентрической системы мира от геоцентрической?
В гелиоцентрической системе отсчёта движение небесных тел рассматривается относительно Солнца, а в геоцентрической — относительно Земли.
В гелиоцентрической системе мира по Копернику за центр Вселенной принимается Солнце, а Земля и другие планеты движутся вокруг него, одновременно вращаясь вокруг своих осей.
4. Как объяснить смену дня и ночи на Земле в гелиоцентрической системе?
В гелиоцентрической системе мира (по системе мира Коперника) видимое движение по небу Солнца днём и звёзд ночью, т. е. смена дня и ночи, объясняется вращением Земли вокруг своей оси
Время, за которое земной шар делает полный оборот, называется сутками.