Проверка гипотезы о виде распределения
Характеристики распределений
Равномерное распределение
Графическое представление 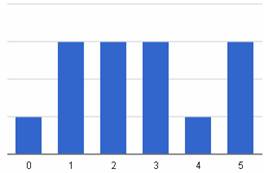 Функция плотности равномерного распределения 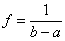 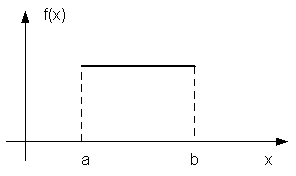 | Математическое ожидание: M[X] = (a+b)/2 Дисперсия: 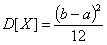 |
Нормальное распределение
Графическое представление 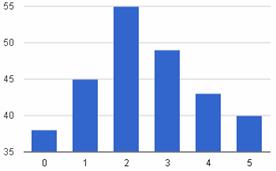 Плотность распределения 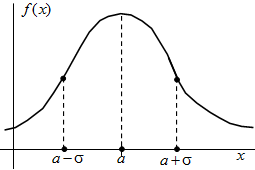 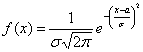 | Математическое ожидание: M[X]=a 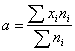 Дисперсия: D[X] = σ 2 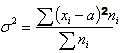 Запись Х |
N( a ; σ) означает, что случайная величина Х распределена по нормальному закону с параметрами a и σ.
Показательное распределение
Графическое представление 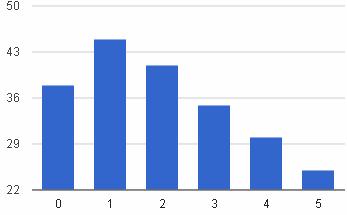 Плотность распределения 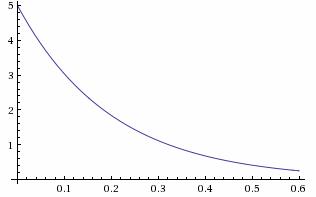 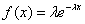 | Математическое ожидание: M[X] = 1/λ Дисперсия: D[X] = 1/λ 2 |
Распределение Пуассона
Биномиальное распределение
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
Пример 1. Нормальным или гауссовым распределением называется непрерывное распределение, плотность которого имеет вид
φ(x)– функция Гаусса (таблица),
Параметры a и σ имеют смысл математического ожидания и среднего квадратичного отклонения.
2. Справедливы формулы:
Ф(x)– интеграл вероятностей, таблица.
Обратим внимание, что Ф(-x)=–Ф(x), Ф(x)=0.5 при x>5.
3. Правило трех сигм: P(|X-a|>3ε)=0.0027 – т.е. вероятность отклонения нормально распределенной величины от математического ожидания более чем на 3σ практически равна нулю.
Главная особенность, выделяющая нормальный закон среди других законов распределения, состоит в том, что он является предельным, к которому приближаются другие законы при весьма часто встречающихся условиях.
Выбираем в качестве начала интервала 6.07, так как именно на этот интервал приходится наибольшее количество
Наиболее часто встречающееся значение ряда – 6.16
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше
Таким образом, что 25% единиц совокупности будут меньше по величине 5.86
Q2 совпадает с медианой, Q2 = 6.1
Остальные 25% превосходят 6.26
Децили (децентили)
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9
Таким образом, что 10% единиц совокупности будут меньше по величине 5.76
Каждое значение ряда отличается от другого не более, чем на 0.22
Дисперсия
Среднее квадратическое отклонение
Каждое значение ряда отличается от среднего значения 6.08 не более, чем на 0.25
Коэффициент вариации
ИДЗ-12. Статистическое распределение случайной величины и его числовые характеристики
Представлены статистические данные. Требуется: 1) составить дискретный вариационный ряд, при необходимости упорядочив его; 2) определить основные числовые характеристики ряда; 3) дать графическое представление ряда в виде полигона (гистограммы) распределения; 4) сформулировать содержательные выводы.
Прим. 1) При проверке статистической гипотезы о виде распределения принять уровень значимости a = 0,05; 2) Для числовой обработки данных рекомендуется использовать подходящий математический пакет, например, электронную таблицу MS Excel.
1.Увлеченный статистической наукой студент путем опроса получил исходные («сырые») статистические данные по росту и весу 20 своих одногруппников:
| № п/п |
| Рост, см |
| Вес, кг |
| № п/п |
| Рост, см |
| Вес, кг |
После упорядочения вариационного ряда требуется изучить распределение студентов по росту.
2.Результаты контрольных измерений веса пирожных в кафе приведены в таблице:
| Вес, г | 20,0 | 20,2 | 20,4 | 20,6 | 20,8 | 21,0 | 21,2 | 21,4 | 21,6 | 21,8 | 22,0 |
| Кол-во пирожных |
Помимо основного задания требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
3.Имеются следующие данные о размере семьи работников цеха (число человек в семье):
3 4 5 2 3 6 4 2 5 3 4 2 7 3 3 6
2 3 8 5 6 7 3 4 5 4 3 3 4.
4.Хронометраж операций пайки радиаторов на ремонтном предприятии дал следующие результаты:
| Время пайки, мин. | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | Итого |
| Кол-во радиаторов |
5.Имеются следующие данные о возрастном составе группы студентов вечернего отделения:
18 38 28 29 26 38 34 22 28 30
22 23 35 33 27 24 30 32 28 25
29 26 31 24 29 27 32 25 29 20.
6.По предприятию получены данные о расстоянии перевозки партий груза в международном сообщении (км) за некоторый период:
560 1060 420 1410 1500 400 3800 700 1780 450
449 285 1850 2200 800 1200 1540 1150 180 452
452 2500 300 400 900 1800 452 1850 1225 220
1800 300 920 1400 1400 480 850 200 400 1440
420 1700 1615 3500 300 320 600 965 450 245.
7.Имеются следующие данные о распределении продовольственных магазинов региона по размеру товарооборота за месяц:
| Группы магазинов по товарообороту, млн. руб. | 40– 50 | 50– 60 | 60– 70 | 70– 80 | 80– 90 | 90– 100 | 100– 110 | 110– 120 | 120– 130 | 130– 140 |
| Число магазинов |
8.На телефонной станции проводились наблюдения над числом Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1;4; 3; 3; 1; 4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3; 2; 7; 2; 0; 0; 1; 3; 3; 1; 2; 4; 2; 0; 2; 3; 1; 2; 5; 1; 1; 0; 1; 1; 2; 2; 1; 1; 5.
9.По автотранспортному предприятию, осуществляющему перевозку грузов автомобилями КамАЗ-5320 грузоподъемностью 16 т, имеются следующие данные о весе партий груза (т):
8 11 14 6 10 13 12 16 15 16
16 10 16 13 14 16 16 4 16 14
5 13 11 2 16 8 16 7 14 16.
10.В результате метеонаблюдений получено статистическое распределение дневных температур в июне месяце:
| Температура, °С | 20º | 23º | 24º | 26º | 27º | 30º |
| Число дней |
11.Получены данные об урожайности ржи на различных участках поля:
| Урожайность ржи, ц/га | 9 – 12 | 12 – 15 | 15 – 18 | 18 – 21 | 21 – 24 | 24 – 27 |
| Доля участка в общей площади, % |
12.Имеются следующие данные о часовой интенсивности движения автомобилей на автомагистрали (авт./час):
140 99 80 140 218 218 340 92 152 120 130
50 110 130 96 48 48 36 60 30 86 102
90 210 220 261 261 282 312 68 80 131 190.
13.Известно распределение золотых медалистов, окончивших в 2001 году школы Ярославской области, по районам:
| Кол-во золотых медалистов |
| Кол-во районов |
14.Имеются следующие данные о количестве заявок на автомобили технической помощи по дням:

11 2 5 14 7 2 8 10 2 6
10 8 3 13 11 8 8 2 9 8
5 14 4 10 12 6 8 2 8 7
9 2 8 4 6 13 5 3 12 2
2 7 9 8 5 8 6 10 11 5.
Помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
15.Обработка детали №37 производится в цехе на токарном полуавтомате. На 25 января получены следующие данные о размере обработанных деталей (в отклонениях от номинала):
| Отклонения от номинала (в сотых долях мм) | 0 – 2 | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | 10 – 12 | 12 – 14 |
| Число деталей |
Для характеристики технологического процесса, помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
16.Имеются следующие данные о величине межремонтного пробега автомобилей ЗИЛ-133:
Для организации технологического процесса ремонта автомобилей, помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
17.Распределение рабочих предприятия по размеру месячного дохода следующее:
Помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
18.Имеются данные наблюдения над числом посетителей сайта академии в течение 40 дней: 72, 76, 101, 123, 74, 64, 111, 122, 74, 68, 65, 107, 65, 119, 71, 77, 67, 104, 108, 128, 72, 85, 80, 123, 65, 90, 76, 84, 105, 104, 122, 128, 107, 86, 79, 80, 87, 109, 107, 94.
19.Распределение промышленных предприятий города по численности работников следующее:
Требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
20.Измерение роста 100 студентов – первокурсников университета дало следующие результаты:
| Рост, см | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |
| Число студентов |
Требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
21.В опытах по рассеянию a-частиц на мишени получены данные по числу a-частиц, достигших счетчика в указанном секторе:
| № сектора |
| Кол-во a-частиц |
22.Распределение рабочих цеха по проценту выполнения норм выработки выглядит следующим образом:
| % выполнения норм | 50-70 | 70-90 | 90-110 | 110-130 | 130-150 | 150-170 |
| Число рабочих |
Выполняет ли производственный план цех в целом?
23.Для определения «общего интеллекта» школьникам предлагалось раскрыть геометрические закономерности. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:
| Кол-во баллов |
| Кол-во школьников |
24.Тренер по легкой атлетике должен решить, кого из двух спортсменов выбрать для стометровой дистанции в предстоящих соревнованиях. Тренер свое решение должен принять на основании пяти забегов между атлетами:
| Анна (сек.) | 12,1 | 12,0 | 12,0 | 16,8 | 12,1 |
| Ирина (сек.) | 12,3 | 12,4 | 12,4 | 12,5 | 12,4 |
а) Основываясь на этих данных, кого из атлетов следует выбрать тренеру и почему? б) Если тренер знал о падении Анны на старте в четвертом забеге, то следует ли учесть это?
25.Предположим, что вследствие ошибки данные, содержащие сведения о среднемесячной заработной плате продавцов (тыс. руб.) в девяти торговых компаниях, имеют вид:
13, 15, 14, 17, 13, 16, 15, 16, 61.
Показать, как эта ошибка влияет на числовые характеристики вариационного ряда. Каковы истинные (скорректированные) характеристики ряда?
26.Увлеченный статистической наукой студент путем опроса получил исходные («сырые») статистические данные по росту и весу 20 своих одногруппников:
| № п/п |
| Рост, см |
| Вес, кг |
| № п/п |
| Рост, см |
| Вес, кг |
После упорядочения вариационного ряда требуется изучить распределение студентов по весу.
27.На основе данных анализа эффективности работы 50-и предприятий города по изменению реальной заработной платы на них в отчетном году (в % к предыдущему году), получен следующий статистический ряд:
| № | Эр[%] | № | Эр[%] | № | Эр[%] | № | Эр[%] | № | Эр[%] |
28.Имеются опытные данные о числе звонков в службу аварийной помощи в течение рабочего дня:
| Интервалы (часы смены) |
| Число звонков |
Требуется построить теоретическую кривую равномерного распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
29.Имеются результаты опроса группы молодёжи, состоящей из 200 человек, о возрасте первого употреблении наркотиков. Результаты представлены в виде интервального вариационного ряда:
Требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
30.Результаты исследования длительности оборота (в днях) оборотных средств торговых фирм города Ярославля представлены в сгруппированном виде:
Требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Литература
1. Андерсон Дж.А. Дискретная математика и комбинаторика.: Пер. с англ. М.: Изд. Дом «Вильямс», 2004. – 960 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшее образование, 2006. – 404 с.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшее образование, 2006. – 404 с.
4. Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистики: учеб. пособие. М.: Финансы и статистики, 2004. – 336 с.
Контрольная работа по «Статистике»
Автор работы: Пользователь скрыл имя, 18 Ноября 2013 в 19:01, контрольная работа
Описание работы
Задание 1 Имеются следующие данные по 20 малым предприятиям.
С целью изучения зависимости между оборачиваемостью оборотных средств и полученной прибылью на малых предприятиях произвести группировку предприятий по оборачиваемости оборотных средств образовав, пять групп с равными интервалами. По каждой группе и всей совокупности подсчитайте: 1. число заводов; 2. среднюю оборачиваемость оборотных средств; 3. размер прибыли – всего и в среднем на одно предприятие. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Содержание работы
Файлы: 1 файл
статистика1.docx
Муниципальное образовательное учреждение
Высшего профессионального образования
По дисциплине «Статистика»
Имеются следующие данные по 20 малым предприятиям:
Продолжительность оборота в днях
Прибыль предприятия, млн. руб.
С целью изучения зависимости между оборачиваемостью оборотных средств и полученной прибылью на малых предприятиях произвести группировку предприятий по оборачиваемости оборотных средств образовав, пять групп с равными интервалами. По каждой группе и всей совокупности подсчитайте: 1. число заводов; 2. среднюю оборачиваемость оборотных средств; 3. размер прибыли – всего и в среднем на одно предприятие. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Группировку предприятий на пять равных групп произвели по оборачиваемости оборотных средств. В каждую группу попало по 5 предприятий. Для каждой группы была подсчитана средняя оборачиваемость оборотных средств, размер прибыли: всего и в среднем на одно предприятие (см. табл.).
Подсчет средней оборачиваемости оборотных средств и среднего размера прибыли вели по простейшей формуле средней:
Распределение автомобилей автотранспортного предприятия по величине суточного пробега за 25 сентября следующее:
Суточный пробег автомобиля, км.
Определите средний суточный пробег одного автомобиля.
1. (150*12+170*36+190*28+210*25) /(12+36+28+25)=183 км.
2) размах вариации = 210-150=60 км
Для вычисления других показателей составьте расчетную таблицу.
По предприятию имеются следующие данные за два месяца:
Фонд заработной платы, руб.
Средняя месячная заработная плата, руб.
Фонд заработной платы, руб.
Определите изменение (в %) среднего уровня месячной заработной платы рабочих и служащих, а также средней заработной платы работников предприятия в феврале по сравнению с январем.
Средний уровень заработной платы рабочих в январе месяце составлял 1867 рублей. Изменение заработной платы рабочих равно 94 %.
Средний уровень заработной платы служащих в январе месяце составлял 487 рублей 50 копеек. Изменение заработной платы служащих в феврале месяце по сравнению с январем составило 164 %.
Имеются следующие данные о величине межремонтного пробега автомобилей:
Величина межремонтного пробега, тыс.км.
По приведенным данным определить среднюю величину межремонтного пробега, показатели моды и медианы, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию, коэффициент осцилляции, коэффициент вариации, относительное линейное отклонение. Дать графическое изображение ряда в виде гистограммы и кумуляты.
Величина межремонтного пробега, тыс. км
Число автомобилей (f)
Число автомобилей в % к итогу
Середина интервала (Х)
Средняя величина межремонтного пробега рассчитывается по формуле:
Средняя величина межремонтного пробега автомобилей равна 127,52 тыс. км.
Мода рассчитывается по формуле:
Имеются следующие данные о ежеквартальной выплавке чугуна по заводу в текущем году:
Выплавка чугуна, тыс. т
Определить: 1. абсолютный прирост цепной и базисный; 2. средний абсолютный прирост; 3. средний уровень ряда; 4. темп роста; 5. темп прироста; 6. средние темпы роста и средние темпы прироста; 7. абсолютное значение одного процента прироста. Сделать прогноз для первого квартала следующего года, применив метод аналитического выравнивания по прямой. Сделать выводы.
1. Абсолютную величину прироста уровня механизации относительно предшествующего года.
2. Темпы роста и прироста (цепные и базисные) уровня механизации за указанный период.
3. Абсолютные значения одного процента прироста.
4. Средний за период уровень механизации.
5.Среднегодовой темп роста уровня механизации за период.
6. Построить графическое изображение динамического ряда.
7. Результаты вычислений оформить итоговые статистические таблицы.
Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для отображения динамики строят ряды динамики (хронологические, временные), которые представляют собой ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. В нем процесс экономического развития изображается в виде совокупности перерывов непрерывного, позволяющих детально проанализировать особенности развития при помощи характеристик, отражающих изменение параметров экономической системы во времени.
Составными элементами ряда динамики являются показатели уровней ряда и периоды времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени.
Существуют различные виды рядов динамики. Их можно классифицировать по следующим признакам.
1. В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.
Примером рядов динамики указанных выше видов являются данные табл. 2.1.
2. В зависимости от того, как выражают уровни ряда состояние явления на определенные моменты времени (на начало месяца, квартала, года и т. п.) или его величину за определенные интервалы времени (например, за сутки» месяц, год и т. п.), различают соответственно моментные интервальные ряды динамики.
Примером интервального ряда динамики являются данные, приведенные в табл. 2.1.
Из различного характера интервальных и моментных рядов динамики вытекают некоторые особенности уровней соответствующих рядов.
Уровни интервального ряда динамики абсолютных величин характеризуют собой суммарный итог какого-либо явления за определенный отрезок времени. Они зависят от продолжительности этого периода времени, и поэтому их можно суммировать к не содержащие повторного счета.
Отдельные же уровни моментного ряда динамики абсолютных величин содержат элементы повторного счета, например, число вкладов населения, учитываемых за январь, существует и в настоящее время, являясь единицами совокупности и в июне. Что это делает бессмысленным суммирование уровней моментах рядов динамики
Методические указания для студентов по проведению практических занятий по дисциплине «Статистика» (стр. 20 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
I Для построения кривой Лоренца необходимо выполнить следующие дополнительные расчеты: абсолютные показатели числа единиц в группах и размерах признака (общая сумма активов) выражаются в относительных величинах (в долях или процентах к итогу) и определяются их накопленные значения. Результаты этих преобразований представлены в таблице
Распределение коммерческих банков по размеру капитала
Группы банков по размеру активов,
Общая сумма активов
Кривая Лоренца представлена на рис. 3.7. На график нанесены накопленные значения двух рядов (таблица графы 4 и 7). При соединении всех точек получена кривая, отражающая процесс Концентрации капитала.
3.1 Имеются следующие данные о размере семьи работников цеха (число человек в семье):
1) составить дискретный вариационный ряд;
2) определить показатели центра распределения, показатели вариации;
3) дать графическое изображение ряда в виде полигона распределения.
Сформулировать краткие выводы.
3.2 Хронометраж операций пайки радиаторов на ремонтном предприятии дал следующие результаты
а) среднее время пайки радиатора; б) медиану и моду; в) относительный показатель вариации.
Дать графическое изображение ряда в виде гистограммы и полигона частот.
3.3 Имеются следующие данные о возрастном составе группы студентов вечернего отделения:
1) построить интервальный ряд распределения;
2) дать его графическое изображение в виде гистограммы и кумуляты;
3) определить численное значение моды и медианы, используя графическое изображение.
3.4 По предприятию получены данные о расстоянии перевозки партий груза в междугородном сообщении (км):
Для анализа работы предприятия требуется:
1) построить интервальный ряд распределения партий груза по дальности перевозки, определив величину интервала по формуле Стерджесса;
2) дать графическое изображение ряда;
3) исчислить показатели центра распределения и показатели вариации.
3.5 Имеются следующие данные о распределении продовольственных магазинов региона по размеру товарооборота за месяц (табл. 3.28).
Требуется вычислить средний месячный размер товарооборота магазинов региона, дисперсию и коэффициент вариации.
Группы магазинов по товарообороту, млн. руб.
3.6 По автотранспортному предприятию, осуществляющем перевозку грузов автомобилями КамАЗ-5320 грузоподъемностью 16 т, имеются следующие данные о весе партий груза (т):
1) построить интервальный ряд распределения партий груза по весу;
2) вычислить для построенного ряда показатели центра распределения и вариации.
Сформулировать вывод об использовании автомобилей КамАЗ-5320.
3.7 Выходной контроль качества поступающих комплектующих изделий дал следующие результаты:
Вычислить дисперсию доли брака по каждой поступившей партии.
3.8 Распределение рабочих двух участков по стажу работы следующее:
Определить, на каком участке состав рабочих по стажу работы более однороден.
3.9 Заработная плата 10 рабочих бригады характеризуется следующими данными:
Месячная заработная плата каждого рабочего за март, руб.
3 252; 3 548; 3 600; 3 400
3 450; 3 380; 3 260; 3 700; 3 250; 3 372
Проверить правило сложения дисперсий и указать, велико ли влияние профессии на различие в уровне заработной платы.
3.10 Имеются следующие данные о часовой интенсивности ^движения автомобилей на автомагистрали (авт/ч):
1) построить интервальный ряд распределения;
2) вычислить: среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
3.11 Имеются следующие данные о заработной плате рабочих автотранспортного предприятия за январь:
Средняя месячная заработная
Определить общую дисперсию заработной платы рабочих предприятия, а также сопоставить однородность двух групп рабочих по уровню месячной заработной платы.
3.12 Имеются следующие данные о количестве заявок на автомобили технической помощи по дням:
1) построить: а) интервальный ряд распределения суточного количества заявок на автомобили технической помощи, определив величину интервала группировки по формуле Стерджесса; б) теоретическую кривую нормального распределения;
2) проверить соответствие эмпирического и теоретического распределений по критерию К. Пирсона. Сформулировать вывод.
3.13 Средняя величина в совокупности равна 15, среднее квадратическое отклонение равно 10. Чему равен средний квадрат индивидуальных значений этого признака?
3.14 Средняя величина признака в совокупности равна 13, а средний квадрат индивидуальных значений этого признака равен 174. Определить коэффициент вариации.
Чему равна средняя величина признака?
3.16 Дисперсия признака равна 25, средний квадрат индивидуальных значений равен 250.
Чему равна средняя?
3.17 Средняя величина признака равна 2600 единицам, а коэффициент вариации равен 30%.
Определить дисперсию признака.
3.18 Общая дисперсия равна 8,4. Средняя величина признака для всей совокупности равна 13. Средние по группам равны соответственно 10, 15 и 12. Численность единиц в каждой группе составляет 32, 53 и 45. Определить среднюю внутригрупповую дисперсию.
Вычислите дисперсию себестоимости изделий в целом по фирме.
3.20 Имеются следующие данные о размере заработной платы рабочих цеха за апрель:



