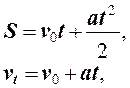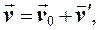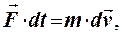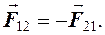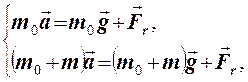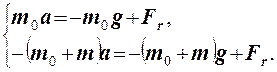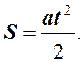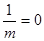Изучение законов поступательного движения на машине Атвуда
Страницы работы
Содержание работы
Лабораторная работа №3
ИЗУЧЕНИЕ ЗАКОНОВ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА
Цель работы: проверить закон пути при равноускоренном прямолинейном движении и второй закон Ньютона.
Приборы и принадлежности: машина Атвуда и набор грузов.
Прямолинейное равноускоренное движение характеризуется постоянным линейным ускорением и равным нулю нормальным ускорением (an = 0, aτ = const).
Законы кинематики для равноускоренного движения имеют вид:
Скорость тела в разных системах координат определяется законом сложения скоростей Галилея
где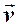 
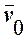
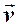
— скорость тела относительно неподвижной системы отсчета; 
— скорость подвижной системы отсчета относительно неподвижной; — скорость тела относительно подвижной системы отсчета.
Закон сложения скоростей Галилея и законы динамики Ньютона выполняются в системах отсчета, которые называются инерциальными.
Системы отсчета называются инерциальными, если они находятся в покое или движутся равномерно прямолинейно относительно какой-то другой инерциальной системы.
Первый закон Ньютона: всякое тело находится в состоянии покоя или равномерного движения, пока и поскольку другие тела не выведут его из этого состояния.
Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Мерой инерции является масса.
Второй закон Ньютона: ускорение, с которым движется тело под действием силы, прямо пропорционально действующей силе и обратно пропорционально массе тела.
или 
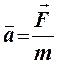
Третий закон Ньютона: силы, с которыми два тела действуют друг на друга, равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей центры масс 
2. ОПИСАНИЕ УСТАНОВКИ
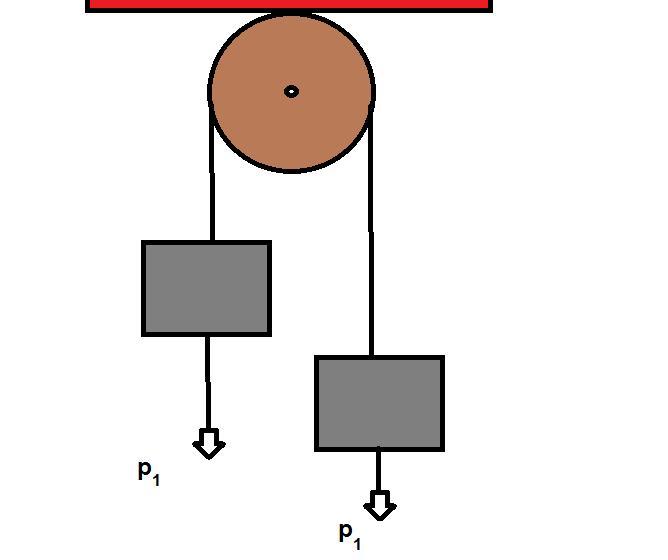
Значение ускорения можно установить из следующих соображений. На каждый груз будут действовать две силы: сила тяжести и сила реакции нити (см. рис. 1).
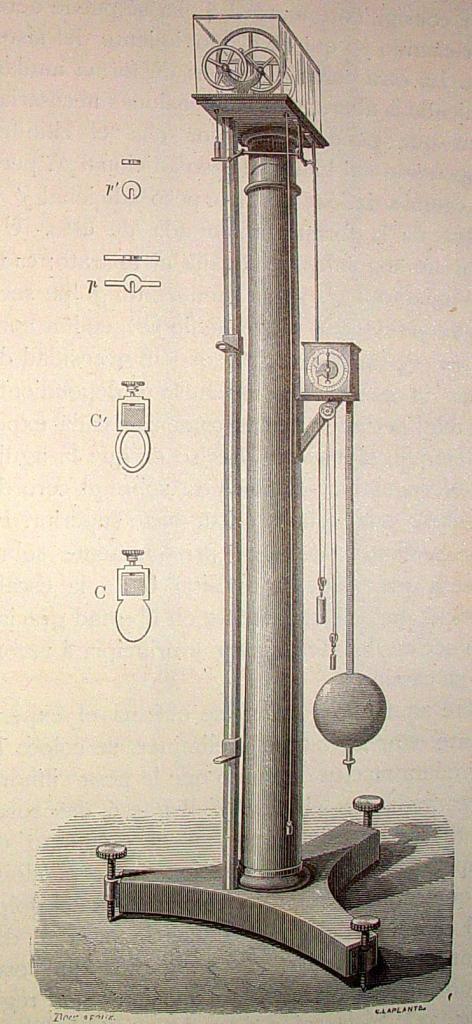
Рис. 1. Машина Атвуда
Под действием равнодействующей этих сил грузы движутся ускоренно, силами трения пренебрегаем. Если предположить, что нить нерастяжима, то ускорения правого и левого грузов будут равны по значению и противоположны по знаку. Кроме того, если считать блок невесомым, то силы натяжения нити справа и слева будут одинаковы. На основании второго закона Ньютона можно записать:
Спроектируем cилы на ось У. Тогда уравнения динамики примут вид:
Решением этой системы линейных уравнений будет ускорение
(1)
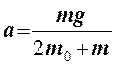
Итак, ускорение прямо пропорционально весу перегрузка mg и обратно пропорционально массе системы тел (2m0 + m).
На лабораторной установке можно изменять массу перегрузка, а также производить измерения на разных отрезках пути.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1. Проверить закон пути равноускоренного движения
Закон показывает квадратичную зависимость пути от времени
Ускорение же системы определяется по формуле (1) и зависит от массы системы. Если масса системы и масса перегрузка не изменяется, то система движется с одинаковым ускорением на разных участках пути.
Для выполнения задания 1 положите на правую платформу прибора (рис. 1) перегрузок m.
2) Установите платформу с перегрузком в самое верхнее положение, а фотодиод 5 установите на заданном расстоянии S на стойке. (Расстояние можете выбрать произвольно).
3) Измерьте время падения грузов на расстоянии S1 с помощью электронного секундомера 4. Запишите время t1 в табл. 1,
4) Повторите опыт, установив платформу на других расстояниях Si.
Методические указания к лабораторной работе «Машина Атвуда»
Экспериментальная проверка основных уравнений и законов поступательного движения тела в поле сил земного тяготения, определение ускорения свободного падения лабораторной установке – машине Атвуда.
Время движения грузов измеряется с помощью ручного или стационарного секундомера.
Для выполнения работы машина Атвуда должна быть установлена строго вертикально, что легко проверить по параллельности шкалы и нити.
Второй закон Ньютона в проекциях на вертикальную ось для каждого из тел системы (рис.2) в предположении невесомости блока, отсутствия силы трения и нерастяжимости нити дает:
(1)
(2)
Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то
(3) 
Третье соотношение часто называют законом перемещений: «Перемещение при равноускоренном движении прямо пропорционально квадрату времени движения».
Соотношение (3) может быть проверено экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение, с которым движется тело, прямо пропорционально равнодействующей действующих на него сил и обратно пропорционально массе этого тела».
Подставляя a i в (2) получаем следующую формулу:
(4)
(5)
— сумма проекций на ось Z всех сил, действующих на вращающиеся тело; α- угловое ускорение блока; J – его момент инерции
(6)
Выразим из уравнения (1) разность сил натяжения ( T 1 – T 2 ) и подставив ее в уравнение (6) получим:
(7)
Выразим ускорение грузов a :
(8)
Учитывая, что значение момента инерции блока
(9),
k- коэффициент распределения массы блока относительно оси вращения (k
11) 
Задание 1. Проверка второго закона Ньютона.
Поскольку ускорение движения является функцией двух переменных – силы и массы, то изучение второго закона Ньютона выполняется путем раздельного исследования двух зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе системы и 2) зависимости ускорения от массы системы при постоянной действующей силе.
Исследование зависимости ускорения от силы при постоянной массе
Измерения и обработка результатов
3. Измеряют время равноускоренного движения системы на пути, например, 1 метр. Все данные заносят в таблицу 1.3 отчета.
4. Пользуясь законом путей (1.6), вычисляют ускорение а.
5. Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.
6. Строят график зависимости ускорения движения от действующей силы. Точку ( F =0, a =0) на графике не откладывают. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод о том, что ускорение действительно прямо пропорционально силе.
7. По угловому коэффициенту полученной прямой определяют массу системы и сравнивают ее реальной массой.
Исследование зависимости ускорения от массы при постоянной силе
Измерения и обработка результатов
1. Все опыты проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе. Ускорение системы измеряется также как и в предыдущем задании.
2. Для изменения массы системы одновременно на правый и левый груз кладут дополнительные одинаковые грузы. Все данные записывают в таблицу отчета.
3. График обратно пропорциональной зависимости ускорения от массы представляет собой гиперболу, которую невозможно идентифицировать. Для проверки предположения об обратно пропорциональной зависимости между ускорением и массой 
необходимо построить график зависимости ускорения от обратного значения массы системы: a = f (М -1 ). Подтверждением предположения является прямолинейность этого графика.
4. По угловому коэффициенту полученной прямой определяют значение приложенной силы и сравнивают ее с реально действующей в системе
Задание 2. Определение ускорения движения грузов
В полученном уравнении прямой 
коэффициент k равен половине ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов ( a =2 k ) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет.
Задание 3. Определение ускорения свободного падения
(Выполняется по результатам измерений и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и перегрузка, а также ускорение движения системы, из формулы (3) найдите ускорение свободного падения. Результаты занесите в отчет. В выводе сравните полученный результат с табличной величиной.
Для нахождения погрешности измерения величины ускорения свободного падения Δ g используем формулу:
12) 
где 
; 
; 
; 
;
– частные производные функции
Проанализируйте результаты своих наблюдений и сформулируйте вывод.
Контрольные вопросы
Какое движение называется поступательным?
Дайте определение инерциальной системы отсчета. Приведите примеры ИСО.
Сформулируйте первый закон Ньютона. Приведите примеры его проявления.
Дайте определение инертной массы тела. Гравитационной? От чего и как зависит масса тела?
Сформулируйте второй закон Ньютона. Приведите варианты его математической формы.
Покажите все силы, действующие на один из грузов в машине Атвуда, и составьте для него уравнение динамики.
Запишите систему уравнений динамики для машины Атвуда с учетом момента инерции блока. Силы трения в блоке?
Изучение законов поступательного движения на машине Атвуда: формулы и пояснения
Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Что такое машина Атвуда?
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.
Вам будет интересно: Пространственная экономика: описание специальностей и структура
Вам будет интересно: Что такое подполье? Подпольная организация «Молодая гвардия». Антифашистское движение
Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
Где m – инерционная масса тела, a – ускорение.
Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.
Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
Проверка решения уравнений динамики
Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
Откуда ускорение определяется однозначно:
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
T = (m2*F1 + m1*F2)/(m1 + m2).
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
ТЕЛ В ПОЛЕ ТЯЖЕСТИ НА МАШИНЕ АТВУДА
ИССЛЕДОВАНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ
Принадлежности: экспериментальная установка машины Атвуда, набор грузов и перегрузков.
 |
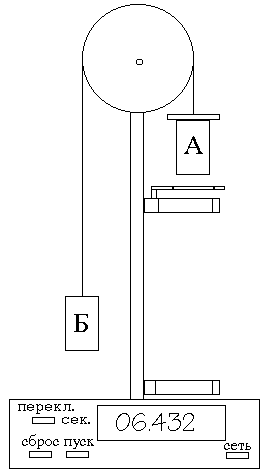Машина Атвуда предназначена для исследования закона движения тел в поле земного тяготения. Естественнее всего, конечно, изучить этот закон, исследуя свободное падение тел. Этому мешает, однако, большая величина ускорения свободного падения. Поэтому такой опыт возможен либо при очень большой высоте прибора (намного большей, чем высота комнаты), либо при помощи специальных методов, позволяющих точно измерять небольшие промежутки времени (доли секунды). Машина Атвуда позволяет избежать этих трудностей и замедлить движение до удобных скоростей. Устройство машины Атвуда изображено на рис. 1.
Легкий алюминиевый блок свободно вращается вокруг оси, укреплённой в верхней части стойки. Через блок перекинута тонкая нить, на концах которой висят грузы А и Б, имеющие равные массы М. На груз А может одеваться один или несколько перегрузков. Система грузов в этом случае выходит из равновесия и начинает двигаться ускоренно.
В начале опыта система удерживается неподвижно с помощью электромагнита. Выключение тока, текущего через электромагнит, приводит нить с грузами в движение, что достигается нажатием кнопки на передней части панели прибора.
Найдём закон движения груза А. При расчётах будем пользоваться неподвижной системой координат, центр которой совмещен с осью блока. Ось ОХ направим вниз.
 |
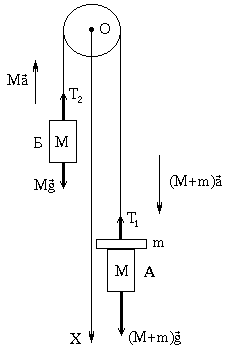Пусть масса перегрузка, лежащего на грузе А, равна m (рис.2)
На груз А действуют две силы: сила тяжести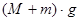 
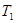
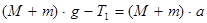
и сила натяжения нити 
. По второму закону Ньютона:
(1)
где a – ускорение груза А.
(2)
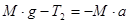
При невесомом блоке натяжения T1 и T2 равны друг другу:
(3)
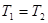
Вычитая из (1) выражение (2) с учетом (3) получим:
(4)
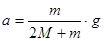
Движение груза происходит, таким образом, равноускоренно и подчиняется уравнению (4). Ускорение a при небольших перегрузках существенно меньше g, поэтому его легче измерить.
Формула (4) может служить для определения ускорения g. Эксперимент осложняется, однако тем, что не существует простых способов прямого измерения ускорения a. Воспользуемся, поэтому, для определения a равноускоренным характером движения и будем измерять путь S и время движения t. При движении без начальной скорости они связаны соотношением:
(5)
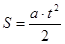
Цель работы заключается, таким образом, в том, чтобы, установив на опыте равноускоренный характер движения (пропорциональность S и t 2 ), определить входящее в (5) ускорение и вычислить с его помощью по формуле (4) ускорение свободного падения.
Это найденное из эксперимента значение a не может быть, однако, непосредственно использовано для определения g, т.к. ускорение зависит не только от a, но и от трения в оси блока.
Величину силы трения можно оценить, замечая наибольшую величину перегрузка m, ещё не вызывающего движения системы. Этот способ не может, однако, быть применён для измерения силы трения, поскольку мешающее опыту трение скольжение скольжения отнюдь не равно трению покоя.
Ясно, что получить хорошие результаты опыта можно только при том условии, если вес перегрузка (силы, вызывающей движение) во много раз больше силы трения. Сила трения определяется в основном весом груза M, а не весом перегрузка. Увеличивая вес перегрузка, мы улучшаем поэтому условия опыта (следует также иметь ввиду вес нити, вообще говоря, не намного меньший веса перегрузка. Вес нити влияет на движение сложным образом, т.к. длина её с каждой стороны блока зависит от времени. Это влияние так же как и влияние силы трения, уменьшает ростом m.).
Величину перегрузка следует поэтому всячески увеличивать; но m не может быть выбрано очень большим, т.к. движение при этом становиться слишком быстрым, и точность измерения времени оказывается недостаточной. Лучше всего поэтому производить измерения с не очень тяжёлым перегрузком m и найти предел, к которому стремится вычисленное g при увеличении m до больших значений, которые на опыте непосредственно применяться не могут. Проще всего находить предел графически. Для этого следует построить график, в котором по оси абсцисс откладывается величина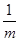 
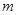
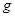
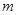
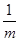
, а по оси ординат – найденное при данном 
значение 
. Проведённую через экспериментальные точки кривую нужно экстраполировать (продолжить) к большим значениям , т.е. к малым значениям , практически к 
Дата добавления: 2015-09-07 ; просмотров: 1355 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ