Динамика
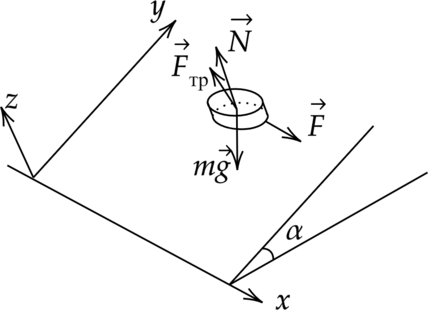
Направим ось \(Oy\) вдоль наклонной плоскости вверх, ось \(Ox\) вдоль наклонной плоскости вправо, а ось \(Oz\) перпендикулярно наклонной плоскости.
Запишем второй закон Ньютона на все три оси: \[\begin
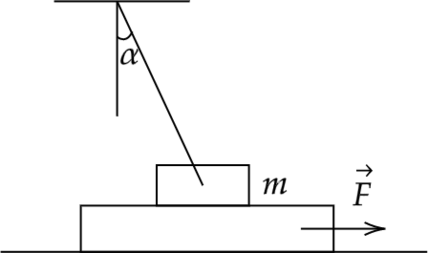
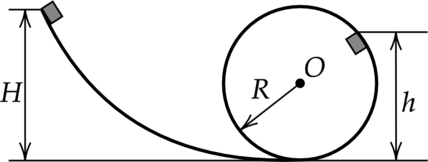
+M\vec Средняя плотность планеты Плюк равна средней плотности Земли, а первая космическая скорость для Плюка в 2 раза больше, чем для Земли. Чему равно отношение периода обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, к периоду обращения аналогичного спутника Земли? Объем шара пропорционален кубу радиуса ( \(V \sim R^3\) ). Период обращения находится по формуле: \[T=\dfrac<2 \pi r> Небольшой кубик массой \(m = 1,5\) кг начинает скользить с нулевой начальной скоростью по гладкой горке, переходящей в «мёртвую петлю» радиусом \(R = 1,5\) м (см. рисунок). С какой высоты \(Н \) был отпущен кубик, если на высоте \(h = 2 \) м от нижней точки петли сила давления кубика на стенку петли \( F = 4 \) Н? Сделайте рисунок с указанием сил, поясняющий решение. Ответ дайте в метрах. Так как центр масс остается неподвижен, то периоды обращения планеты и звезды равны. Запишем закон всемирного тяготения для звезды и планеты \[F=G\dfrac Гоночный автомобиль массой 2500 кг едет по шоссе со скоростью 360 км/ч вдоль экватора. Насколько отличаются силы давления автомобиля на полотно дороги при его движении с запада на восток и с востока на запад? Угловая скорость вращения Земли \(7,3 \cdot 10^<-5>\) рад/с. Ответ дайте в Па и округлите до сотых. Имеется недеформированная пружина длиной \(L = 20\) см и жёсткостью \(k = 100\) Н/м, груз массой \(m = 0,2\) кг, а также вращающийся с частотой 1,5 Гц массивный диск. На каком максимальном расстоянии от центра диска можно положить на него груз, прикрепив его пружиной к центру диска, чтобы груз оставался неподвижным относительно диска? Коэффициент трения между грузом и диском Размерами груза пренебречь. Сделайте схематический рисунок с указанием сил, действующих на груз. “Основная волна 2020 Вариант 2” “Основная волна 2020 Вариант 3” 7 мая в клубе военной части было проведено мероприятие « дети войны», к 65-й годовщине великой победы. слова светланы алексеевич из книги «дети войны» наиболее полно дадут характеристику данному мероприятию и его целям: « беспощадной волей войны оказывались в пекле страданий и невзгод и осилили, вынесли то, что, казалось бы, и взрослому преодолеть не всегда под силу.война отбирает у мальчиков и девочек детство – настоящее, солнечное, с книгами и тетрадями, смехом, играми и праздниками.самой природой, условиями существования рода человеческого детям предназначено жить в мире! что помнят они? что могут рассказать? должны рассказать. потому что и сейчас где-то тоже рвутся бомбы, свистят пули, рассыпаются от снарядов на крошки, пыль дома и горят детские кроватки. потому что и сегодня хочется кому-то большой войны, вселенской хиросимы, в атомном огне которой дети испарялись бы, как капли воды, засыхали бы, как страшные цветы.как сохранить планету людей, чтобы детство никогда больше не называлось войной? » и самый главный ответ на поставленный вопрос звучит так: « нужно помнить ужасы войны».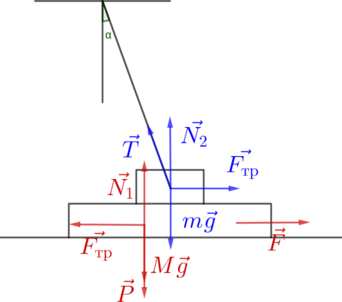
Найдем отношение периода обращения вокруг планеты Плюк к периоду обращения вокруг Земли. \[\dfrac
Первая космическая скорость находится по формуле: \[v_1=\sqrt
где \(m\) и \(M\) – масса спутника и планеты
Масса же находится по формуле: \[M=\rho V,\] \(\rho\) – средняя плотность планеты.
С учетом того, \(V \sim R^3\) имеем \[\dfracДинамика (страница 2)
Кроме того эта сила взаимодействия будет создавать центростремительное ускорение для планеты и звезды, мы воспользуемся только для звезды \[G\dfracГоночный автомобиль массой 2500 кг едет по шоссе со скоростью 360 км / ч вдоль экватора, на сколько отличаются силы давления автомобиля на полотно дороги при его движении с запада на востока и с востока на запад?
Ответы