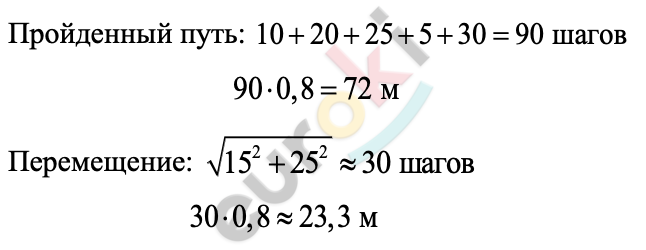Московская олимпиада школьников по физике 7-11 класс задания и ответы 3-го отборочного этапа 2020-2021
ПОДЕЛИТЬСЯ
Задания и ответы для московской олимпиады школьников МОШ по физике 7, 8, 9, 10, 11 класс третьего отборочного этапа 2020-2021 ученый год, официальная дата проведения олимпиады: 15.01.2021-17.01.2021 (с 15 по 17 января 2021 года).
Для 7 класса — 9 заданий, для 8-11 класса — 10 заданий для выполнения.
Ссылка для скачивания заданий для 7-11 класса: скачать
Ссылка для скачивания ответов для 7-11 класса: скачать
Московская олимпиада школьников по физике 7-11 класс третий тур отборочного этапа 2020-2021 задания и ответы:
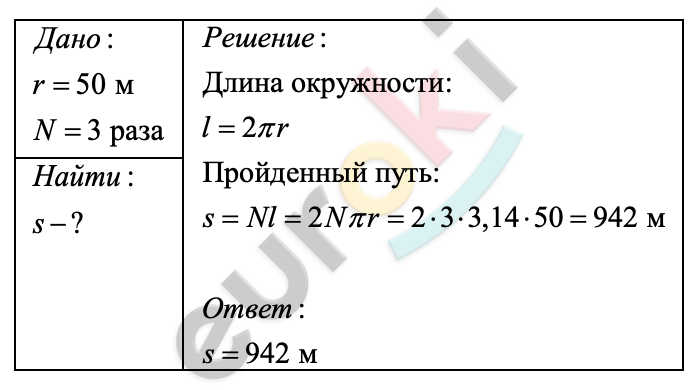
1)Переведите в СИ: 15 г/л (грамм на литр).
2)Чему равна цена деления шкалы секундомера, изображенного на рисунке?
3)Эскалатор метро движется вверх со скоростью 0,75 м/с. С какой скоростью относительно эскалатора должен двигаться пассажир, чтобы быть неподвижным относительно стоящих пассажиров на соседнем эскалаторе, который движется вниз со скоростью 0,75 м/с?
4)Чему равна средняя скорость тела за первые 7 с. Укажите вариант ответа, в котором стоит значение, наиболее близкое к найденному вами.
Московская олимпиада школьников по физике 8 класс третий тур отборочного этапа 2020-2021 задания и ответы:
1)Чему равна средняя скорость тела на первой половине пути? Укажите вариант ответа, в котором стоит значение, наиболее близкое к найденному вами.
3)Три кубика имеют одинаковые массы, и внутри одного из них имеется полость. Известно, что ρ2 g = 10 «> g = 10 Н/кг. Ответ выразите в см, округлите до десятых.
8)Рабочий удерживает за один конец бревно так, что этот конец находится на уровне живота рабочего, а второй конец бревна лежит на земле. При этом рабочему приходится действовать на бревно вертикальной силой 100 Н. Если рабочий положит бревно на землю, подойдёт к противоположному концу бревна, поднимет его и будет держать на уровне головы, то окажется, что он действует на бревно вертикальной силой 300 Н. Найдите массу бревна. Ускорение свободного падения g = 10 «> g = 10 Н/кг. Ответ выразите в кг, округлите до целого числа.
10)Два одинаковых калориметра имеют температуру 20℃. В первый из них налили 50 г воды с температурой 50℃. Когда установилась тепловое равновесие, половину воды перелили в другой калориметр. Когда в нем установилась тепловое равновесие, его температура стала 25℃. Определите теплоемкость калориметра. Удельная теплоемкость воды равна 4200 Дж/(кг•℃). Ответ выразите в кДж/℃, округлите до сотых.
Московская олимпиада школьников по физике 9 класс третий тур отборочного этапа 2020-2021 задания и ответы:
1)Законы движения двух материальных точек заданы уравнениями: x1=−3t−3t2 (м) и x2=−3+2t (м). Какой из рисунков согласуется с данными уравнениями в начальный момент времени?
3)Закрытый сосуд, частично заполненный водой, и две гири уравновешены на рычажных весах. Нарушится ли равновесие весов, если вода испарится?
4)На рисунке представлен график зависимости температуры олова от времени. Укажите участок, на котором внутренняя энергия увеличивается?
5)Общий ток в участке цепи I=160 мA. Определите показание I4 четвёртого амперметра А4. Приборы идеальные.
6)Машине длиной 4 м, едущей по шоссе, попадается на пути автобус длиной 14 м, который движется со скоростью 85 км/ч. Водитель автомобиля снижает скорость до 85 км/ч и начинает готовиться к обгону. Какое время понадобится для безопасного обгона, если скорость автомобиля при обгоне не превышает 95 км/ч, а автомобиль ускоряется равномерно так, что за каждую секунду скорость автомобиля увеличивается на 5 км/ч, и после окончания обгона скорость автомобиля равна 95 км/ч? При безопасном обгоне расстояние между автомобилем и автобусом равно 15 м до и после обгона. Ответ выразите в секундах, округлите до десятых.
8)В кастрюле находится 5 кг воды. На её нагревание от температуры 40℃ до температуры 41℃ требуется 10 с. Найдите время, которое понадобится для того, чтобы нагреть эту воду от температуры 90℃ до температуры 91℃. Мощность плиты 2500 Вт. Считайте, что тепловые потери пропорциональны разности температур воды и окружающей среды. Температура окружающей среды равна 20℃. Теплоёмкостью кастрюли можно пренебречь. Удельная теплоёмкость воды 4200 Дж/(кг·℃). Ответ выразите в секундах, округлите до целого числа.
9)Школьник решил починить ёлочную гирлянду, в которой перегорела одна лампочка. Гирлянда с 18 лампочками питается от сети с напряжением 230 В. На лампочках написан их тип: 13,6 В и 0,13 А. К сожалению, точно таких же лампочек у школьника не было. Какие из нижеперечисленных типов лампочек подошли бы для замены перегоревшей лампочки:
10)Комната имеет длину 4 м и высоту 3 м. На одной стене комнаты вертикально висит зеркало. Человек стоит на расстоянии 1 м от зеркала лицом к зеркалу. Какой должна быть минимальная высота зеркала, чтобы человек мог видеть находящуюся за его спиной стену в полную высоту (от пола до потолка)? Ответ выразите в см, округлите до целого числа.
Московская олимпиада школьников по физике 10 класс третий тур отборочного этапа 2020-2021 задания и ответы:
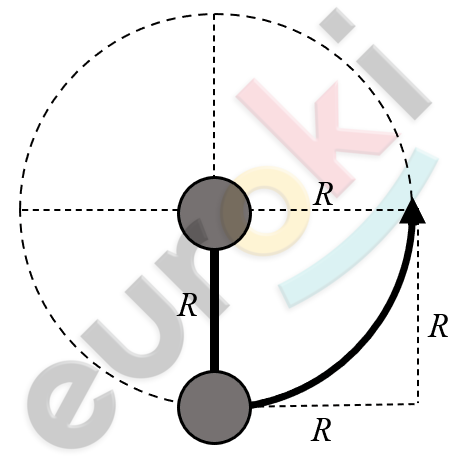
3)Клин массой 2 m «> 2 m покоится на гладком горизонтальном столе. На клин аккуратно ставят брусок массой m «> m и отпускают без начальной скорости. Клин и брусок приходят в движение. Выберите правильное утверждение.
4)В два одинаковых котелка налито одинаковое количество воды при одинаковой температуре. Один котелок расположен на уровне моря, а второй находится высоко в горах. Выберите правильное утверждение.
5)Имеются четыре фонарика, в каждом из которых есть по три одинаковые лампочки. Соединение лампочек в каждом случае различно. Какой фонарик светит тусклее всего, если напряжения батарей в фонариках одинаковые?
6)Из кормового и носового зенитных орудий, расположенных на верхней палубе неподвижного крейсера, под одним и тем же углом 30° к горизонту прямо по курсу одновременно производятся два выстрела. Начальная скорость снаряда носового орудия равна 100 м/с, кормового 200 м/с. Найти наименьшее расстояние между снарядами в процессе полёта, если длина палубы (расстояние между орудиями) равна 100 м. Ответ выразите в м, округлив до целого числа. Ускорение свободного падения считайте равным 10 м/с2. Сопротивлением воздуха пренебречь. Траектории снарядов лежат в одной вертикальной плоскости.
8)На одинаковых нитях подвешены практически в одной точке два маленьких, упругих шарика массами m и M (m
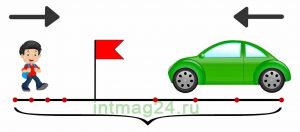
Движущийся автомобиль некоторое время ехал в направлении
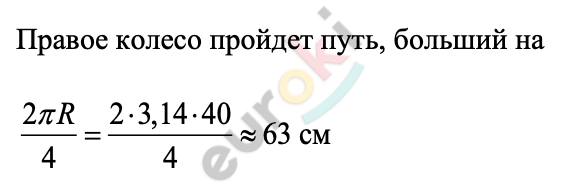
Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, двигаясь с постоянной по модулю скоростью 36 км/ч. Радиус кривизны моста равен 40 м. Из приведённого ниже списка выберите все правильные утверждения, характеризующих движение автомобиля по мосту.
1) Равнодействующая сил, действующих на автомобиль в верхней точке моста, сонаправлена с его скоростью.
2) Сила, с которой мост действует на автомобиль в верхней точке моста, меньше 20 000 Н и направлена вертикально вниз.
3) В верхней точке моста автомобиль действует на мост с силой, равной 15 000 Н.
5) Ускорение автомобиля в верхней точке моста направлено противоположно его скорости.
Переведем скорость
Рассмотрим рисунок, поясняющий движение автомобиля по выпуклому мосту.
1. Неверно. Равнодействующая сил реакции опоры N и силы тяжести mg по второму закону Ньютона сонаправлена с вектором ускорения. А т. к. автомобиль движется по окружности, то ускорение направлено к центру окружности, т. е. вниз. Следовательно, и равнодействующая направлена вниз. Скорость автомобиля при движении по окружности направлена по касательной (в данном случае — горизонтально).
2. Неверно. Сила, с которой мост действует на автомобиль — сила реакции опоры — направлена вертикально вверх.
3. Верно. Сила, с которой автомобиль действует на мост, равна весу тела. По третьему закону Ньютона P = N. Найдём силу реакции опоры по второму закону Ньютона Центростремительное ускорение равно
Значит, Р = 15 кН.
4. Верно. (см. пункт 3).
5. Неверно. Вектор ускорения направлен вертикально вниз, вектор скорости — горизонтально (см. пункт 1).
ГДЗ по физике 7 класс Генденштейн, Булатова БИНОМ Лаборатория знаний Задание: §7 Механическое движение
Вопросы к параграфу
Нельзя однозначно ответить на вопрос, покоится или движется пассажир едущего автобуса, т.к. необходимо рассматривать пассажира относительно какого-либо тела. Таким образом, пассажир покоится относительно корпуса автобуса, но движется относительно придорожных столбов.
а) самолет не движется относительно сидящего в кресле пассажира;
б) самолет движется относительно стюардессы, идущей по салону.
Придорожные столбы, корпус автобуса и сидящие пассажиры движутся относительно идущего пассажира. Автомобиль, обгоняющий автобус со скоростью, на 5 км/ч большей скорости автобуса, покоится относительно идущего пассажира.
Человек, относительно которого дом движется сверху вниз, находится в поднимающемся лифте.
Пассажир мог сделать 3 различных предположения: что поезд на соседнем пути начал движение, что поезд с пассажиром начал движение, что оба поезда начали движение одновременно с различными скоростями. Проверить предположение можно, посмотрев на здание вокзала и оценив наличие движения относительно него.
а) птицы покоятся относительно друг друга;
б) пассажиры самолета покоятся относительно друг друга и борта самолета;
в) гребец и лодка покоятся относительно друг друга;
г) мотоциклист и мотоцикл покоятся относительно друг друга;
д) девушка и корпус поезда покоятся относительно друг друга.
Траектория движения автомобиля становится видимой при его резком разгоне или остановке, когда протекторы оставляют следы на асфальте из-за сильного трения.
Прямолинейное движение: падение камня без начальной скорости, поездка автомобиля по прямой дороге.
Криволинейное движение: бег спортсмена по стадиону, колебания маятника.
Из этого не следует, что траектория движения Саши была криволинейной, т.к. Саша мог идти по прямой дороге, меняя направление движения на противоположное несколько раз.
Дополнительные вопросы и задания
Базовый уровень
Рассмотрим человека, поднимающегося на эскалаторе в метро. Он неподвижен относительно поручня эскалатора, других поднимающихся людей на том же самом эскалаторе и на соседнем поднимающемся эскалаторе. Он движется относительно ламп в вестибюле, людей на соседнем спускающемся эскалаторе, и людей, поднимающихся пешком.

Траектория ручки относительно бумаги:
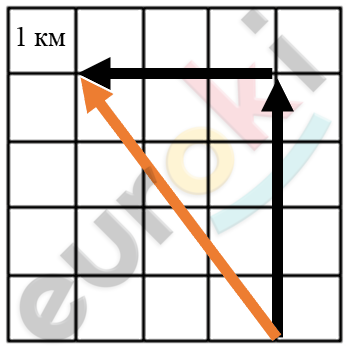
Траектория падающего камня относительно Земли:
Траектория корабля, совершившего кругосветное путешествие, будет замкнутой относительно Земли.
Повышенный уровень
Велосипедисты не движутся относительно друг друга, т.к. расстояния между велосипедистами не изменяются.
Траектория корабля, совершившего кругосветное путешествие за полгода, будет
а) замкнутой относительно Земли;
б) незамкнутой относительно Солнца.
Траектория человека, вышедшего из дома и вернувшегося обратно, будет
а) замкнутой относительно дома;
б) незамкнутой относительно самолета, который за это время пролетел от Москвы до Астрахани.


Чтобы траектория корабля, совершившего кругосветное путешествие, была замкнута не только относительно Земли, но и относительно Солнца, путешествие должно длиться целое число лет.
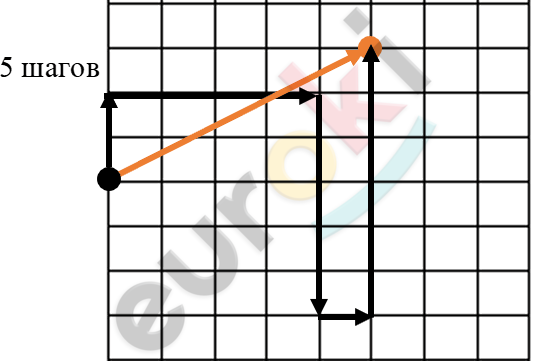
Для этих друзей перемещение будет одинаковым.
Перемещение:
Высокий уровень
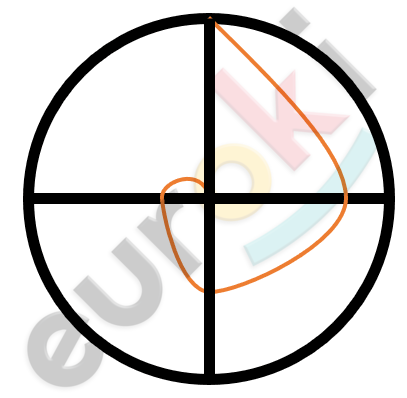
Божья коровка двигалась вдоль минутной стрелки и проползла ее от начала до конца, следовательно, пройденный божьей коровкой путь равен 6 см.
Домашняя лаборатория
Опыт: держа карандаш неподвижно, двигать лист бумаги так, чтобы карандаш нарисовал окружность. Траектория острия карандаша относительно стола – точка; относительно листа бумаги – окружность.
© 2021Copyright. Все права защищены. Правообладатель SIA Ksenokss.
Адрес: 1069, Курземес проспект 106/45, Рига, Латвия.
Тел.: +371 29-851-888 E-mail: [email protected]
Задачи на движение

— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов. Получить карточки с задачами разных видов можно по ссылке.