Где и через сколько времени они встретятся?
встреча произойдет если Х1 = Х2
Движение двух тел заданы уравнениями?
Движение двух тел заданы уравнениями.
Найти t и место встречи.
Уравнения : X1 = 12t X2 = 120 + 10t.
Постройте график скоростей движения этих тел.
Движение тела задано уравнением x = 1 + 3t + 2t ^ 2(м)?
Движение тела задано уравнением x = 1 + 3t + 2t ^ 2(м).
Какой будет его скорость через промежуток времени 5 с после начала отсчета времени?
4. Движение тела задано уравнением x = 3t + 2t2(м)?
4. Движение тела задано уравнением x = 3t + 2t2(м).
Какой будет его скорость через промежуток времени 5 с после начала отсчета времени?
Скорость движения тела задана уравнением v = 8 + 2t?
Скорость движения тела задана уравнением v = 8 + 2t.
Запишите уравнение движения тела, если тело в начальный момент времени находится на расстоянии 20 м от начального отсчёта.
43 БАЛЛА ЗА РЕШЕНИЕ?
43 БАЛЛА ЗА РЕШЕНИЕ!
Координаты тел в момент времени 5 секунд
Где и когда встретятся два тела?
графики скорости и графики движения
Движение тела задано уравнением x = 1 + 3t + 2t(м)?
Движение тела задано уравнением x = 1 + 3t + 2t(м).
Какой будет его скорость через промежуток времени 5 с после начала отсчета времени?
Зависимость перемещения тела от времени при прямолинейном движении задано уравнением Sx = 2t + 5t2 путь пройденный телом за 5 с равен?
Зависимость перемещения тела от времени при прямолинейном движении задано уравнением Sx = 2t + 5t2 путь пройденный телом за 5 с равен.
Движение двух тел заданы уравнениями х1 = 2t ; х2 = 4 + 2t ; каковы начальные координаты тел?
Движение двух тел заданы уравнениями х1 = 2t ; х2 = 4 + 2t ; каковы начальные координаты тел?
С какой скоростью движутся тела?
Когда они встретятся?
Движение двух автомобилей по шоссе задано уравнениями x1=2t+0,2t^2 и x2=80-4t
Условие задачи:
Движение двух автомобилей по шоссе задано уравнениями \(x_1=2t+0,2t^2\) и \(x_2=80-4t\). Найти время и место встречи автомобилей.
Задача №1.7.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Когда эти два автомобиля встретятся, их координаты будут равны. Поэтому, чтобы найти время встречи \(t\) приравняем уравнения.
Решим получившееся квадратное уравнение, для чего найдем дискриминант.
\[D = 900 + 4 \cdot 400 = 2500\]
\[\left[ \begin
t = 10 \; с \hfill \\
t = – 40 \; с \hfill \\
\end
Получили два корня, один из которых не может являться ответом, поскольку он отрицательный. Теперь, чтобы найти место встречи автомобилей, нужно подставить полученное время в любое из уравнений. Будет легче всего, если подставить во второе.
\[x = 80 – 4 \cdot 10 = 40\; м\]
Ответ: 10 с, 40 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
Уточнение. Водитель x1 опомнился и повернул назад при времени t= – 5 c.
И через 5 с “начался” отсчет времени по задаче…
Очевидно водитель x1 хотел предупредить водителя x2 о том, что того ждет впереди…
Почему не учтен второй ответ?
Автомобили (до “начала решения задачи”) встречались 40 с назад… 
40 c назад они ехали в одну сторону. Потом (через некоторое время) водитель x1 “опомнился” (это как раз время t=0) и поехал назад. Вот тут-то через 10 с они и встретились…
Давайте не будем наводить смуту в умах людей и условимся, что в подобных задачах имеет смысл только положительное время (т.е. после начала отсчета).
Просто отрицательное время может появляться в различных задачах, например, на движение тела, брошенного под углом к горизонту, где оно точно не будет иметь смысла, а Вы можете их натолкнуть на поиск объяснения отрицательного корня.
Соглашусь, что некоторый анализ корней уравнения всё же нужен, но переусердствовать тоже не стоит.
Учебники
Журнал «Квант»
Общие
Уровень B
1. Запишите уравнения проекции скорости и перемещения для движений, у которых:
Охарактеризуйте каждое движение.
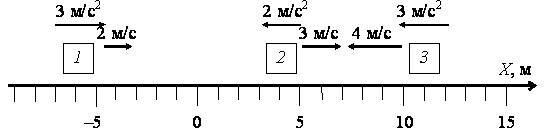
2. Используя данные рисунка 1:
а) найдите координаты тел, их проекции начальных скоростей и ускорений;
б) запишите уравнения проекций скорости, перемещения, координаты (движения) для каждого тела;
в) определите проекции скорости, перемещения и координату каждого тела через 3 с;
г) найдите расстояние через 3 с: между 1-м и 2-м телами; между 2-м и 3-м телами;
д) определите, когда проекции скорости тел будут равны 0 м/с.
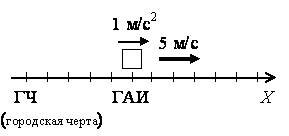
3. Автомобиль, проехав мимо поста ГАИ со скоростью 5 м/с, разгоняется с ускорением 1 м/с 2 по прямолинейному участку пути. Пост ГАИ находится на расстоянии 50 м от городской черты (рис. 2). Найдите его положение относительно городской черты через 30 с после прохождения им поста ГАИ.
6. По прямолинейной дороге в одном направлении едут велосипедист со скоростью 36 км/ч и мотоциклист со скоростью 72 км/ч. В начальный момент времени расстояние между ними было 250 м. Когда и где мотоциклист догонит велосипедиста?
7. По прямому пути в одном направлении движутся два мотоциклиста. Начальное расстояние между ними 20 м. Скорость первого мотоциклиста 5,0 м/с. Второму мотоциклисту для его обгона потребовался 4,0 с. Какова скорость второго мотоциклиста?
8. Заданы уравнения движения для пяти тел. По этим уравнениям определите начальные координаты, проекции начальных скоростей и ускорений тел. Перерисуйте рисунок 3 и расставьте на нем тела соответственно их начальным координатам, обозначьте их начальные скорости и ускорения (модуль и направление).
9. Дано одно из трех уравнений (или проекции скорости, или проекции перемещения, или координаты) для разных тел. По этому уравнению определите начальные координаты, проекции начальных скоростей и ускорений и допишите остальные два уравнения:
11. Скорость прямолинейно движущегося тела выражается уравнением υx = 2,5 + 0,2t. Найдите проекцию перемещения тела через 20 с от начала движения.
Уровень C
1. Движения двух автомобилей по шоссе заданы уравнениями x1 = 2t + 0,2t 2 и x2 = 80 – 4t. Найдите:
а) время и место встречи автомобилей;
б) расстояние между ними через 5 с от начала отсчета времени;
в) координату первого автомобиля в тот момент времени, когда второй находился в начале отсчета.
а) через 40 с после встречи;
Найдите расстояние между ними в эти моменты времени.
4. Из пунктов А и В, расстояние между которыми 120 км, навстречу друг другу выехали два автобуса: первый – в 9 ч утра, а второй – в 9 ч 30 мин утра. Первый двигался со скоростью 40 км/ч, а второй – со скоростью 60 км/ч. Сделайте рисунок. Определите где и когда встретятся автобусы.