Можно ли считать автомобиль материальной точкой: подробный ответ
В физике или математике, когда решают различного рода задачи, то используют те или иные приближения. Одним из таких приближений является понятие о материальной точке. Рассмотрим в статье вопрос, можно ли автомобиль считать материальной точкой.
Понятие о точке материальной
Прежде чем отвечать на вопрос, можно ли считать материальной точкой автомобиль, познакомимся с самим понятием.

С материальными точками начал работать Исаак Ньютон, когда формулировал свои законы поступательного движения в классической механике.
Размерами тела (но не его массой) можно пренебречь, когда необходимо найти ускорение тела, если к нему приложена внешняя сила, или же когда следует рассчитать пройденный им путь. Иными словами, многие вопросы кинематики и динамики линейного движения решаются с помощью понятия материальной точки.
Когда автомобиль можно рассматривать как материальную точку
Можно ли считать автомобиль материальной точкой, если нужно решить задачу на определение его скорости движения, или ускорения, сообщаемое крутящим моментом его двигателя? Да, во всех этих случаях важна только масса транспортного средства, а не его габариты.
Основным критерием, когда можно говорить о материальной точке, а когда нельзя, являются проходимые расстояния. Так, если автомобиль проезжает десятки километров, то, конечно же, его геометрия мало кого интересует.
В каких задачах автомобиль материальной точкой не является
Можно ли считать автомобиль материальной точкой в физике, если рассматривают его столкновение. Нет, нельзя. Более того, в этом случае важны не просто размеры авто, но и механические свойства материала, из которого он изготовлен. Последние определяют энергию поглощения при ударе.
Если рассматривают автомобиль как систему действующих на него внешних сил, тогда о материальной точке также не может быть и речи. Эта ситуация возникает, например, при рассмотрении не только силы тяги, но и сил трения качения колес транспортного средства или сил скольжения, когда автомобиль заходит в поворот на большой скорости.
Таким образом, можно сделать следующий вывод: при рассмотрении кинематики поступательного движения, а также динамики в случае действия одной внешней силы, когда пройденный путь намного больше размеров автомобиля, его можно считать точкой с конечной массой; если задача предполагает наличие нескольких сил, действующих на разные части авто, тогда его габариты учитывать необходимо.
Можно ли считать автомобиль материальной точкой при определении пути. Ответы на частые вопросы
Когда автомобиль считается материальной точкой в решении задач физики и математики
Лучшие ответы на вопрос:
Тело можно считать материальной точкой в том случае, когда его размеры намного меньше расстояния, которое это тело проходит. Когда формой, размерами тело можно пренебречь, они не играют существенной роли.
Автомобиль проходит за t = 2 часа со скоростью V = 80 км/ч путь S = V *t = 80 км/ч * 2 ч = 160 км. В этом решении нигде не используются размеры самого автомобиля, поэтому они не учитываются и сами автомобили могут быть заменены на мат точку.
При обгоне автомобиль нельзя считать материальной точкой. Поскольку, расстояние на котором происходит обгон соизмерим с размерами автомобиля. Автомобиль для обгона должен проехать немного больше длинны автомобиля, который обгоняет. Но, если в условиях задачи не указываются и не используются в расчетах расстояния: обгона и самого автомобиля, то тогда он может считаться материальной точкой.
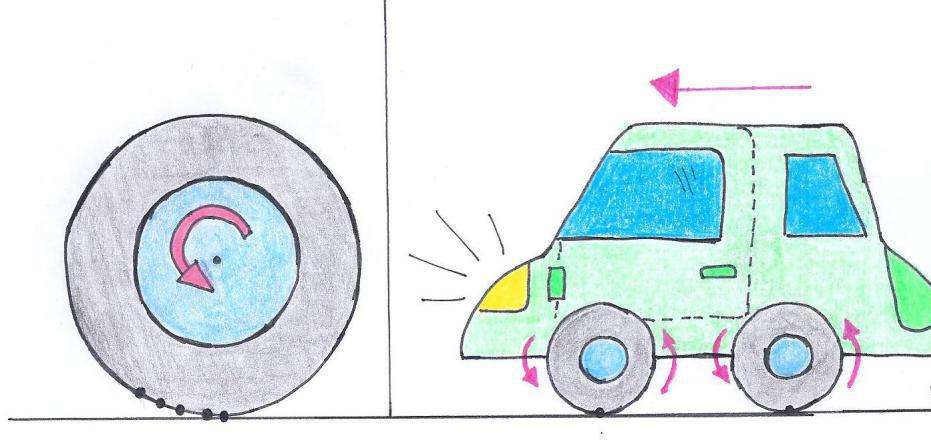
На данной картинке, показаны задачи про автомобили, но размер их в данном случае не имеет никакого значения, поэтому их можно заменить на материальную точку.
Ответ 2. Тело можно считать материальной точкой, если его размерами при описании движения можно пренебречь. Для определения пути нужно знать начальные координаты, скорость, ускорение и время движения; размеры автомобиля не имеют значения. Поэтому в этом случае его можно считать материальной точкой.
Ответ 3. Автомобиль в описанной задаче можно считать материальной точкой. Ведь при движении автомобиля и при расчете задачи мы можем пренебречь его размеры, как это обычно делается в задачах по физике. Так что его можно назвать мат.точкой.
Ответ 4. Да, автомобиль можно и нужно считать материальной точкой для определения пути. В противном случае, провести расчеты будет крайне сложно, если не сказать невозможно.
Вопрос: только автомобиль может быть материальной точкой?
Ответ: нет, любое тело или предмет или живые организмы, размеры которых не нужны или не используются в расчетах тоже могут считаться материальными точками.
То есть, во всех задачах где нужно найти скорость и расстояние пройденного пути, все объекты автомобили, тракторы, велосипеды, корабли, другие транспортные средства, самолеты, поезда и даже все животные и рыбы будут считаться материальной точкой.

Что такое материальная точка
Материальной точкой в физике считается объект, размерами которого можно пренебречь в задаче. Здесь именно такой случай – размерами автомобиля можно пренебречь.
Материальная точка (частица) — обладающее массой тело, размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях исследуемой задачи. Является простейшей физической моделью в механике. Положение материальной точки в пространстве определяется как положение геометрической точки и задаётся радиус-вектором
С какой целью используется понятие “материальная точка”
Понятие материальной точки используется для упрощения условий и решений задач. Если пренебречь размерами реального тела, то нет необходимости рассматривать движение тела при его движении вокруг своей оси (мяч в полёте) или движение каких- то частей тела (колеса автомобиля), если нас интересует с какой скоростью движется тело.
ВОПРОСЫ
1. Обладает ли материальная точка массой? Имеет ли она размеры?
Под материальной точкой в физике понимается тело, размерами которого в условиях данной задачи можно пренебречь. Материальная точка обладает определенной массой, но имеет нулевые (очень малые) размеры.
2. Материальная точка- это реальный объект или абстрактное понятие?
Материальная точка— абстрактное понятие, т.к. в природе все тела обладают определёнными размерами.
3. С какой целью используется понятие «материальная точка»?
Понятие материальной точки используется для упрощения условий и решений задач. Если пренебречь размерами реального тела, то нет необходимости рассматривать движение тела при его движении вокруг своей оси (мяч в полёте) или движение каких- то частей тела (колеса автомобиля), если нас интересует с какой скоростью движется тело.
4. В каких случаях движущееся тело обычно рассматривают как материальную точку?
В данном случае движущееся тело можно рассматривать как материальную точку, если его размеры намного меньше расстояния на которое оно перемещается.
5. Приведите пример, показывающий, что одно и то же тело в одной ситуации можно считать материальной точкой, а в другой- нет.
Если рассматривать, например, движение автомобиля, при его перемещении из города А в город Б, то в данном случае, при определении средней скорости движения автомобиля его можно рассматривать как материальную точку, однако если нас интересует движение автомобиля более подробно, то окажется, что при движении автомобиля, например передние и задние колёса из-за неровностей дороги двигаются по разному (не синхронно).
6. При каком движении тела его можно рассматривать как материальную точку даже в том случае, если проходимые им расстояния сравнимы с его размерами?
Если тело движется поступательно.
7. Что называется материальной точкой?
Материальная точка— это абстрактное понятие обозначающее тело, размеры которого не играют роли в условиях рассматриваемой задачи.
8. В каком случае положение движущегося тела можно задать с помощью одной координатной оси?
Если тело движется прямолинейно.
9. Что такое система отсчёта?
Система отсчёта- это тело отсчёта, связанная с ним система координат и прибор для измерения времени, по отношению к которым рассматривается движение материальных точек или тел.
УПРАЖНЕНИЯ
1. Можно ли считать автомобиль материальной точкой при определении пути, который он прошёл за 2 часа, двигаясь со средней скоростью, равной 80 км/ч? при обгоне им другого автомобиля?
2. Самолёт совершает перелёт из Москвы во Владивосток. Может ли рассматривать самолёт как материальную точку диспетчер, наблюдающий за его движением? пассажир этого самолёта?
3. Когда говорят о скорости машины, поезда и других транспортных средств, тело отсчёта обычно не указывают. Что подразумевают в этом случае под телом отсчёта?
Под телом отсчёта, в данном случае, обычно подразумевают поверхность Земли.
4. Мальчик стоял на земле и наблюдал, как его младшая сестра каталась на карусели. После катания девочка сказала брату, что и он сам, и дома, и деревья быстро проносились мимо неё. Мальчик же стал утверждать, что он вместе с домами и деревьями, был неподвижен, а двигалась сестра. Относительно каких тел отсчёта рассматривали движение девочка и мальчик? Объясните кто прав в споре.
Оба правы. Мальчик выбрал систему отсчёта относительно себя (он был неподвижен), а девочка относительно себя (она была на качелях).
5. Относительно какого тела отсчёта рассматривают движение, когда говорят:
а) скорость ветра равна 5 м/с?
б) бревно плывет по течению реки, поэтому его скорость равна нулю;
в) скорость плывущего по реке дерева равна скорости течения воды в реке;
г) любая точка колеса движущегося велосипеда описывает окружность;
д) Солнце утром восходит на востоке, в течение дня движется по небу, а вечером заходит на западе?
а) относительно поверхности Земли; б) относительно текущей воды; в) относительно поверхности Земли; г) относительно центра (оси) колеса; д) относительно поверхности Земли.
Механика. Механическое движение. Материальная точка. Система отсчета
ГЛАВА I. ЗАКОНЫ ВЗАИМОДЕЙСТВИЯ И ДВИЖЕНИЯ ТЕЛ
Тема: Механика. Механическое движение. Материальная точка. Система отсчета.
Движение тел по наклонной плоскости;
Относительное движение тел.
План изложения нового материала:
Понятие материальной точки; система отсчета;
Относительность и абсолютность движения;
История развития учения о механике.
Во вступительной части учитель рассказывает, что будут изучать учащиеся в этом учебном году, какие задания их ждут. Так же необходимо напомнить технику безопасности на уроках физики и во время проведения лабораторных работ.
Далее необходимо вспомнить, что такое физика.
Основные разделы физики:
Изучение нового материала
Первые дошедшие до нас сочинения по механике, в которых описаны простейшие машины, принадлежат ученым Древней Греции. К ним относится сочинение «Физика» Аристотеля (IV в. до н.э.), в котором впервые введен в науку термин «механика». В III в. до н.э. древнегреческий ученый Архимед впервые применил математику для анализа и описания механических явлений. Архимед сформулировал закон равновесия рычага и закон плавания тел. С этого времени начинается развитие механики как науки.
Новый этап связан с работой Г. Галилея, сформулирован закон инерции, установил законы падения тел и колебаний маятника. Английский физик И. Ньютон, опираясь на работы Галилея и его современников, а так же на результаты своих собственных исследований, создал цельное учение о механическом движении и взаимодействии тел, которое получило название классической механики.
Классическая механика состоит из трех частей: кинематика, динамика, статика.
Слово кинематика происходит от греческого слова kinematos — движение.
Кинематика изучает движение тел без учета тех причин, которые вызывают данное движение.
Основными задачами кинематики являются:
а) Описание с помощью математических формул, графиков или таблиц совершаемых телом движений.
б) Определение кинематических величин, характеризующих это движение.
Для описания движения в кинематике вводятся специальные понятия (материальная точка, система отсчета, траектория) и величины (путь, перемещение, скорость, ускорение), которые важны не только в кинематике, но и в других разделах физики.
— Какие изменения вы замечаете? ( Ночь меняет день, вода при охлаждении замерзает, падают капли, лает собака, едет автомобиль, двигаются литься деревьев в ветреную погоду.)
— Поведем итог: наиболее частые ответы связаны с изменением положения тел относительно друг друга.
Опр. Изменение положения тела в пространстве относительно других тел с течением времени называются механическим движением .
«Дайте мне материю и движение, и я построю Вселенную», говорил французский ученый Рене Декарт (1596-1650). Но что такое движение? Согласно Декарту, «движение, в обычном понимании этого слова, есть не что иное, как действие, посредством которого данное тело переходит с одного места на другое». В наши дни движение иногда определяют как изменение положения тела в пространстве с течением времени. Однако еще Эйнштейн предупреждал, что, согласившись с таким определением, мы «примем на свою совесть не один тяжкий грех», ибо «неясно, что следует понимать здесь под словами «место» и «пространство».
Действительно, представьте, что перед вами на столе лежит яблоко. Кроме вас, в комнате больше никого нет. Закройте глаза на секунду, а затем откройте их. Можно ли утверждать, что яблоко, которое вы снова видите перед собой, продолжает находиться в том же самом месте пространства, в каком находилось за секунду до этого?
Однако одно и то же тело одновременно может и двигаться и не двигаться, если наблюдать его с различных точек зрения.
Пример 1. В купе вагона на столике лежит яблоко. Пассажир видит, что расстояние до яблока с течением времени сохраняется. Яблоко не совершает механического движения. Но с точки зрения провожающего, яблоко движется, т.к. расстояние от яблока до перрона с течением времени растет.
Пример 2. Вы находитесь в классе в покое (сидя за партой) относительно Земли, но движетесь вместе с Землей вокруг Солнца.
Понятие материальной точки. Система отсчета.
Из выше указанных примеров следует: нет, и не может быть абсолютно неподвижных тел.
Даже самое простое движение тела оказывается сложным для изучения. Для того чтобы облегчить исследования, вводят ряд упрощений. Если мы рассматриваем движение автомобиля, длина которого 5 м, прошедшего 100 км, то пройденное им расстояние в 200000 раз больше его собственной длины. Очевидно, что автомобиль можно рассмотреть как точку. В этом случае пользуются термином материальная точка. Но если мы будем исследовать силу сопротивления воздуха, действующего на движущийся автомобиль, считать его материальной точкой нельзя, т.к. сила сопротивления зависит от размеров автомобиля. Материальная точка-это абстрактное понятие, введенное для упрощения изучения многих физических явлений.
Опр. Материальной точкой называют тело, размерами и формой которою в рассматриваемом случае можно пренебречь.
движение большого (малого) бруска по прямой на опоре;
выруливание самолета на взлетную полосу, и его полет из Москвы в Киев;
движение слона в «посудной лавке», и движение Земли по орбите вокруг Солнца.
— Как же определить положение тела (материальной точки)?
В одном древнем документе, относящемуся к началу нашей эры, сказано: «Стань у восточной стены крайнего дома лицом на север, и, пройдя 120 шагов, повернись лицом на восток. Затем, пройдя 200 шагов, вырой яму в 10 локтей и найдешь 100 золотых монет».
— Если бы этот документ попал в Ваши руки, смогли бы найти клад? (У каждого человека разные шаги и локти. Не указан населенный пункт. Местность сильно изменилась. Нет дома, от которого нужно считать.)
Итак, необходимо тело отсчета . Если через него провести оси координат, то положение тела в пространстве можно задать его координатами. Но при движении тела его положение меняется с течением времени. Значит, нужен прибор для измерения времени (часы), связанные с телом отсчета.
Система координат может быть:
При помощи одной координаты определяют положение тела, которое движется по прямой (рис. 1).
При помощи прямоугольной системы координат XOY определяют положение тела на плоскости (рис. 2).
И, наконец, трехмерная система координат определяет положение тела в пространстве (рис. 3).
Относительность и абсолютность движения
бессмысленно говорить о движении тела, не указав тело отсчета, относительно которого рассматривается это движение;
относительно разных тел отсчета (например, Земли, Солнца, самолета и т.д.) одно и то же движение может выглядеть по-разному: разными могут быть траектории движения, пройденные пути, перемещения, скорости и т.д.
Учитель может продемонстрировать относительность движения на примере бруска, неподвижно лежащего на двигающейся тележке (рис.). Брусок неподвижен относительно тележки, но перемещается относительно земли.
Можно рассмотреть траекторию падения мяча относительно точки падения, и сбоку, относительно земли.
Все эти опыты показывают относительность механического движения.
Но механическому движению присуща и абсолютность .
Опр. Абсолютными называют такие свойства движения, которые не зависят от выбора тела отсчета.
Например, если относительно Земли два тела А и В приближаются друг к другу, то их сближение будет происходить и относительно любого другого тела отсчета (автомобиля, Луны, Солнца и т.д.). Другими словами, нельзя найти такое тело отсчета, по отношению к которому эти два тела А и В не сближались бы, а, например, удалялись бы друг от друга. Сближение этих тел имеет абсолютный характер.
Скорость сближения двух тел одинакова и с точки зрения наблюдателя, и из окна поезда. Невозможно найти такую систему отсчета, в которой данные тела не сближались бы, а, например, удалялись друг от друга.
Упражнения и вопросы для повторения
На станке изготавливают спортивный диск. (Не материальная точка.)
Тот же диск после броска спортсмена летит на расстояние 55 м. (Материальная точка.)
Конькобежец проходит дистанцию соревнования. (Материальная точка, но не всегда: не надо забывать про фотофиниш.)
Фигурист выполняет упражнения произвольной программы. (Не материальная точка.)
За движением космического корабля следят из Центра управления полетов на Земле. (Материальная точка.)
За тем же кораблем наблюдает космонавт, осуществляющий с ним стыковку. (Не материальная точка.)
Земля вращается вокруг своей оси. (Нематериальная точка.)
Земля движется по круговой орбите вокруг Солнца. (Материальная точка.)
Качественные задачи на понятие системы отсчета, материальной точки:
В движущемся вагоне пассажирского поезда на столе лежит книга. В покое или движении находится эта книга относительно: а) рельсов; б) стола?
Как движется токоприемник, расположенный на крыше вагона электропоезда, относительно: а) вагона; б) контактного провода?
Автомобиль и комбайн движутся прямолинейно, так что некоторое время расстояние между ними не меняется. Укажите, относительно каких тел они находятся в это время в покое, и относительно каких тел движутся?
Сидящий на вращающемся «чертовом колесе» видит, что колесо относительно него неподвижно, а деревья и строения движутся. С каким телом в данном случае связана система отсчета?
Изобразите схематически траекторию движения точек винта самолета относительно земли.
Приведите примеры задач, в которых спортсмена а) можно считать материальной точкой; б) нельзя считать материальной точкой.
Можно ли при определении объема стального шарика с помощью мензурки считать этот шарик материальной точкой?
Из центра горизонтально расположенного вращающегося диска по его поверхности вдоль радиуса пущен шарик. Каковы траектории шарика относительно земли и диска?
Что изучает механика?
На какие разделы делится механика?
Что изучает кинематика как раздел механики?
Вспомните определение механического движения.
Приведите примеры относительности и абсолютности механического движения.
Что такое материальная точка?
Домашнее задание: § 1, записи в тетради; упр. 1 (учебник, стр. 9); Сборник задач № 137, 142.
Материал для учителя
Кинематики материальной точки
Механическое движение и его характеристики
теория по физике 🧲 кинематика
Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
По типу линии, вдоль которой движется тело, выделяют два вида движения:
По скорости выделяют два вида движения:
По ускорению выделяют три вида движения:
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
Способы описания механического движения
Описать механическое движение можно двумя способами:
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
Перемещение
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).
Математическое определение модуля скорости:

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид :
Отсюда скорость равна:
Подставляем имеющиеся данные и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить