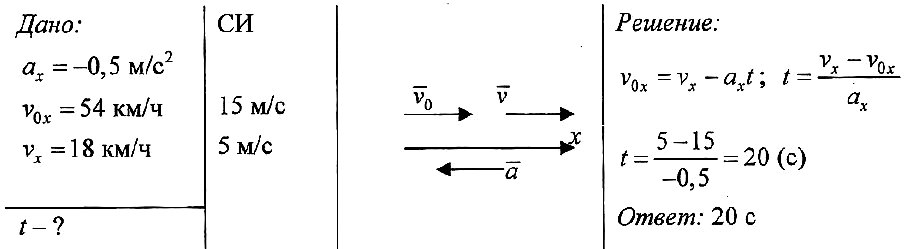
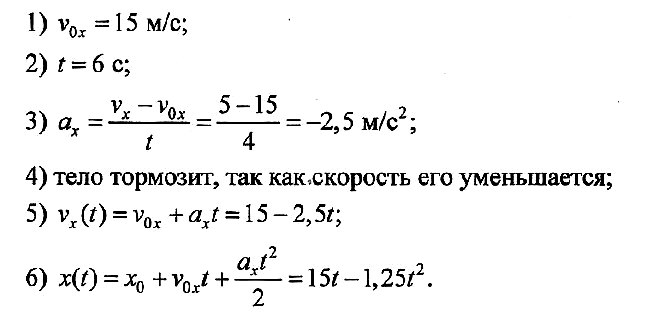Движение автомобиля описывается уравнением x 20 10t постройте график для скорости автомобиля
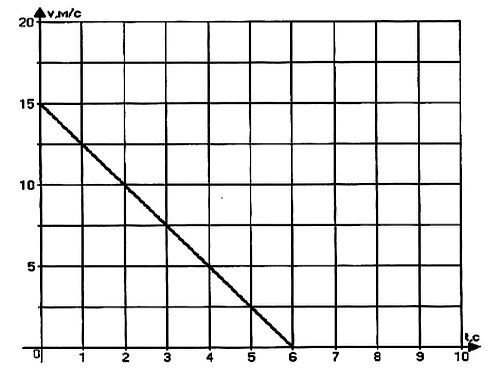
Задача № 3. По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).
Решение:
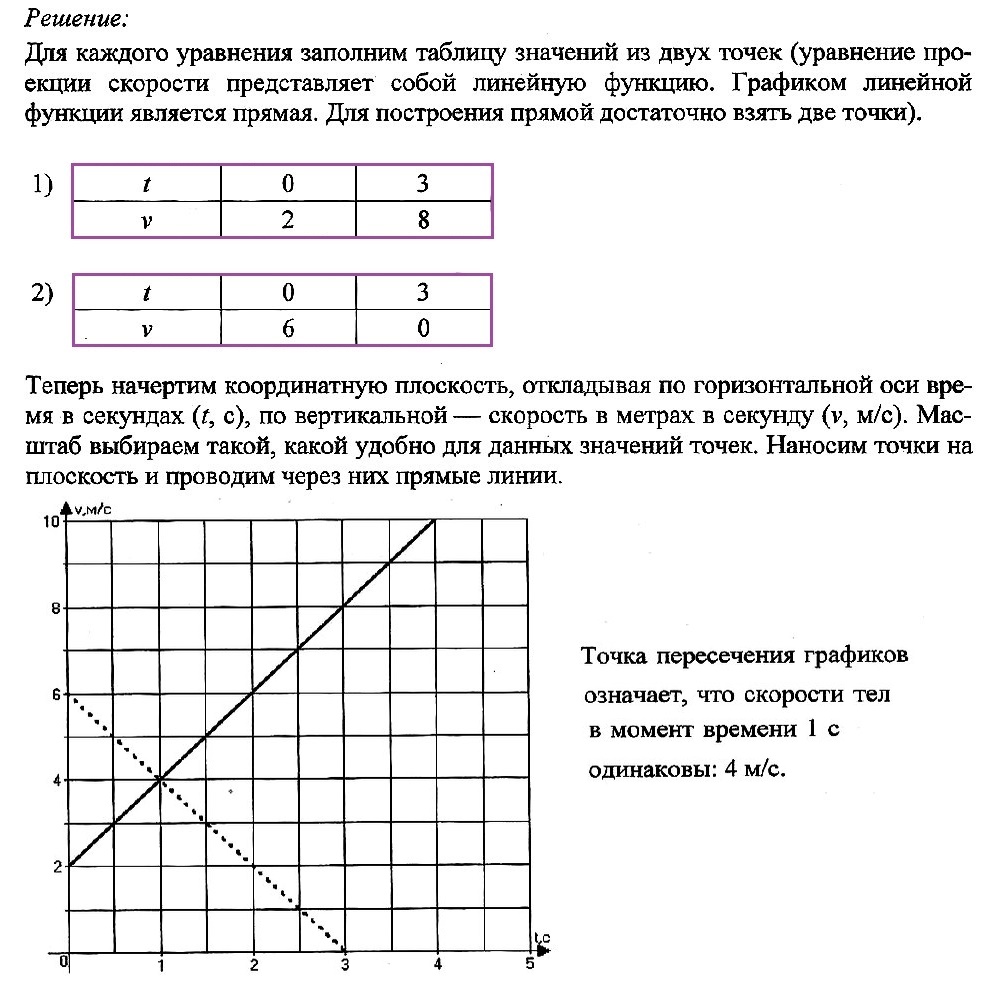
Задача № 4. Движение двух тел задано уравнениями проекции скорости:
v1x(t) = 2 + 2t
v2x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?
Решение:
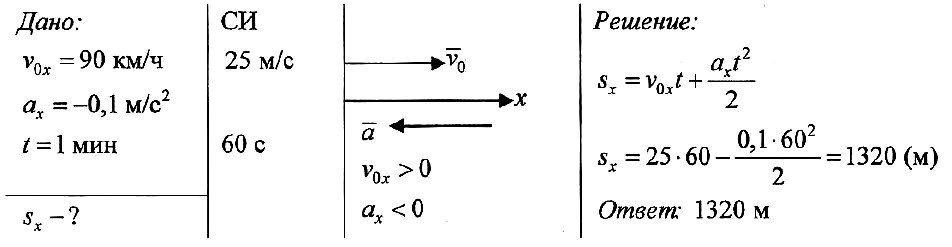
Задача № 7. Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с 2 в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?
Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.
Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).
Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.
Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.
Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:
29 Комментарии
Спасибо за альтернативную точку зрения, не указанную в школьных учебниках физики. Надеюсь, это поможет учащимся расширить свой кругозор в области физики.
Ускорение — это вектор, а он отрицательным быть не может. Но вот проекция ускорения очень даже может быть отрицательной. И, прямо скажем, я не пойму что Вы тут написали, но попахивает каким-то бредом. Хотя бы потому, что at — это приращение скорости, а средняя скорость — это перемещение деленное на время движения, или путь на время движения, если интересует средняя ПУТЕВАЯ скорость. Деление же на 2, в уравнении движения возникает из-за правил интегрирования, которые говорят о том, что интеграл at по dt равен 0.5at^2/
Тело движется прямолинейно под действием постоянной силы 12 Н, при этом зависимость координаты тела от времени имеет вид: (м). Определить: массу тела; импульс тела в момент времени t = 2 c ; среднюю скорость за промежуток времени от t1 = 0 c до t2 = 2 c.
S/tt=F/m. S=? Тело двигалось,или стояло?
….мощность мотора при условиях в задаче. (вес машины…1200 кг)
..машина имела ускорение 4 м/сс.. (для машины-«приличное» ускорение..) F/1200=4 сек.сек. F=4800 кг м./сек. Это=64 л.с. при 100% КПД
КПД ДВС=16 %. 64*6,25=400 л.с. (есть такие моторы. Правда, вес ТАКИХ машин 2,5-3 тонны…) Вот пример «теории и практики». А если вес машины …2650 кг., то мотор должен быть: 4*2650/75*6,25=883 л.с.
Определить тормозную путь,если известны начальная скорость 30 м/сек и замедление 6 м/сек2
V кон.=2at. 30=2*6*t. t=2,5 c. S=att. 6*2,5*2,5. S=37,5 м.
В последней задаче: t= V ср./ a. Vср.=15 м/с. t=15/6=2,5 секунды (быстрее свободного падения…) S=att. 6*2,5*2/5=37,5 м.
(…напутал в решении…)
При «ускорении» 19 м/сс, скорость через 30 сек. будет: Vкон.=2at. 2*19*30. V кон.=1140 м/с. (4104 км/час)
во второй задаче: V нач.=25 м/с. а=0,1 м/сс. t=60 c. S=? (давать надо одно: или «ускорение», или «время»)
решение: S=V ср.*t. 12,5*60=750 м. «ускорение»= V ср./t. 12,5/60. t=0,2 м/сс.
При «а»=0,1 м/сс. t=Vср./a. 12,5/0,1=125 секунд.
S при а=0,2 м/сс. S=att. 0,208*60*60=750 м. (и при разгоне, и при торможении)
S при а=0,1 м/сс. S=att. 0,1/125*125. S=1562,5 м. (и при разгоне. и при торможении)
задача № 9
V нач.=х. V кон.=5х. V ср.=3х. t=2c. S=18 м. V ср.=9 м. х=9/3=3 м/с. V кон.=15 м/с.
a=S/tt=Vср./t a=18/4=9/2=4,5 м/сс
ПРОВЕРКА: S=att. 4,5*2*2=18 м.
Проверка (по Вашему решению): a=6 м/сс. S=att/2. 6*2*2/2=12 м (?)
У Вас не получается, потому что Вы проверяете ответ по своей формуле. Правильная формула проекции перемещения указана в начале статьи и в самой задаче!
Вот такие «анонимы» в средневековье … всех, кто думал не так, как «принято». (текст изменен модератором сайта)
Во второй задаче некорректная формулировка. По факту, даны избыточные данные. «Тормозной путь» соответствует расстоянию до полной остановки, то есть такое понятие подразумевает конечную скорость, равную нулю. А по заданным числам конечная скорость будет равна v0 — a * t = 25 — 0.1*60 = 19 м/c.
Возможно, конкретно в это задаче автор подразумевал под тормозным путём участок, на котором поезд замедлял движение, при этом не до полной остановки. Меня это тоже вначале сбило с толку.
В 11-й задаче проще использовать формулу a = (V-Vo) / t
Даша! V конечная (при равно-ускоренном движении и одной из скоростей=0 ) есть 2at. СРЕДНЯЯ скорость (25+0)/2=12,5 м/с. С такой СРЕДНЕЙ скоростью поезд за минуту (60 сек) пройдёт: 12,5*60=750 м.
Если задачу решать через «а», то t=12,5/0,1=125 секунд. S=V ср.*t. 12,5*125=1562,5 м.
Если поезд (по условию задачи) прошёл 750 м. (до остановки), то его ЗАМЕДЛЕНИЕ скорости (-«а»): S=att 750/60/60. а=0,2 м/сс.
Вывод: давать в условии задачи одно: или «а», или t
С точки зрения физики торможение — это тоже ускорение, только с обратным знаком. Поменяли условие задачи № 2, чтобы не было двусмысленности.
всем доброго времени.
Очень е силен в физике последние лет 25, по этой причине прошу помочь в решении некой задачи!
Дано начальная скорость = 10 м/с.
Вопрос сможет ли тело долететь до высоты 4 м и если сможет то с какой скоростью. Да, полет вертикальный!
На мой взгляд в даны не все условия, но могу и ошибаться.
Спасибо.
Такие задачи рассматриваются в разделе «Задачи на свободное падение» https://uchitel.pro/задачи-на-свободное-падение/
Добавить комментарий Отменить ответ
Конспекты по физике:
7 класс
8 класс
9 класс
10-11 классы
Найти конспект:
О проекте
Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Возрастная категория: 12+
(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!
Урок по физике на тему «Равномерное прямолинейное движение. Уравнения и графики. Мгновенная скорость и ускорение. Свободное падение тел. Движение по окружности.» (10 класс)
Тема: Равномерное прямолинейное движение. Уравнения и графики. Мгновенная скорость и ускорение. Свободное падение тел. Движение по окружности.
Цель: изучить характеристики прямолинейного равномерного движения; сформулировать понятие скорости и ускорения; движение точки по окружности.
1. Характеристики прямолинейного равномерного движения, графики.
2. Скорость при прямолинейном равномерном движении, ускорение.
3. Движение точки по окружности.
Задание для самопроверки.
1. Материальная точка движется равномерно от центра вращающегося диска по его радиусу. В какой системе отсчета траектория точки будет прямой линией?
2. Автомобиль преодолел подъем длиной 200 м с углом наклона к горизонту 30°. Определите перемещение автомобиля в вертикальном и горизонтальном направлениях.
Изложение нового материала
Определение прямолинейного равномерного движения. С прямолинейным равномерным движением Вы уже знакомы из курсов физики и математики предыдущих классов: в большинстве задач на движение рассматривалось именно такое движение. Следует дать определение прямолинейного равномерного движения, привести примеры и подчеркнуть существенный признак такого движения: равенство перемещений в любые сколь угодно малые промежутки времени.
Можно пронаблюдать за равномерным движением воздушных пузырьков в двух стеклянных трубках разного сечения и выяснить, чем отличаются эти равномерные движения. Опыт позволяет получить понятие скорости.
Скорость при прямолинейном равномерном движении. Скорость — одна из основных кинематических характеристик движения материальной точки, определяемая отношением перемещения к интервалу времени, в течение которого оно произошло:
Из этой формулы следует, что
Удобно направить ось х вдоль прямой, по которой движется тело: тогда единственная отличная от нуля проекция скорости
Проекция скорости v x может быть как положительной, так и отрицательной — в зависимости от того, в каком направлении оси х движется тело.
Перемещение при прямолинейном равномерном движении. Формулы для зависимости проекции перемещения s x и координаты х от времени имеют вид:
Вопросы для самопроверки.
Можно ли утверждать, что тело движется прямолинейно равномерно, если оно:
за каждую секунду проходит путь, равный 1 м;
движется вдоль прямой в одном направлении и за каждую секунду проходит путь 3 м?
Какая скорость больше: 15 м/с или 36 км/ч?
Можно ли, зная начальное положение тела и длину пройденного пути, определить его конечное положение?
Задачи для самопроверки
2. Тело движется прямолинейно равномерно. Обязательно ли являются линейными функциями времени: а) пройденный путь; б) модуль перемещения; в) модуль координаты?
Для конспекта студента.
■ Прямолинейным равномерным движением называется движение, при котором тело за любые равные интервалы времени совершает одинаковые перемещения.
■ Скорость прямолинейного равномерного движения равна отношению перемещения тела к интервалу времени, за который совершено это перемещение:
■ Зависимость от времени перемещения, проекции перемещения и координаты тела:
Контрольное задание №1
1) Сколько времени потребуется поезду длиной 450 м, чтобы преодолеть мост длиной 750 м, если скорость поезда 72 км/ч?
2) Один автомобиль, двигаясь со скоростью 16 м/с, проехал туннель за 30 с, а другой автомобиль, двигаясь равномерно, проехал тот же туннель за 24 с. Какова скорость второго автомобиля?
3)Тело движется в отрицательном направлении оси ОХ со скоростью 36 км/ч. Начальная координата равна 20 м. Найдите координату тела через 4 с. Какой путь прошло тело?
Самостоятельная работа № 1
«Прямолинейное равномерное движение»
1. Сколько времени потребуется скорому поезду длиной 150 м, чтобы проехать мост длиной 850 м, если скорость поезда равна 72 км/ч?
2. Двигаясь равномерно прямолинейно, тело за 10 с преодолело 200 см. За сколько часов это тело, двигаясь с той же скоростью и в том же направлении, преодолеет путь 36 км?
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
В каждый данный момент времени движущаяся точка может находиться только в одном определенном положении на траектории. Поэтому ее удаление от начала координат есть некоторая функция времени t . Зависимость между переменными s и t выражается уравнением s = f ( t ). Траекторию движения точки можно задать аналитически, т. е. в виде уравнений: s = 2 t + 3, s = 4 t или графически.
Графики — «международный язык». Овладение ими имеет большое образовательное значение. Поэтому необходимо научиться не только строить графики, но и анализировать их, читать, понимать, какую информацию о движении тела можно получить из графика.
Графики зависимости проекции перемещения от времени.
График функции s x = f ( t ) называется графиком движения.
Наклон графика тем больше, чем больше модуль скорости.
Графики зависимости проекции скорости от времени. Наряду с гра фиками движения часто используются графики скорости v x = f ( t ) . При изучении равномерного прямолинейного движения необходимо научиться строить графики скорости и пользоваться ими при решении задач.
Площадь фигуры, ограниченной графиком u x ( t ) и осью t , численно равна модулю перемещения (рис. 3).
Наряду с графиком скорости очень важны графики координаты движущегося тела, так как они дают возможность определить положение движущегося тела в любой момент времени.
Графики зависимости координаты от времени. График x ( t ) = = x 0 + s x ( t ) отличается от графика s x ( t ) только сдвигом на х 0 по оси ординат. Точка пересечения двух графиков соответствует моменту, когда координаты тел равны, т. е. эта точка определяет момент времени и координату встречи двух тел (рис. 4).
По графикам x ( t ) видно, что велосипедист и автомобиль в течение первого часа двигались навстречу друг другу, а затем — удалялись друг от друга.
Графики пути. Полезно обратить внимание на отличие графика координаты (перемещения) от графика пути. Только при прямолинейном движении в одном направлении графики пути и координаты совпадают. Если направление движения изменяется, то эти графики уже не будут одинаковыми (рис. 5).

Обратите внимание: хотя велосипедист и автомобиль движутся в противоположных направлениях, в обоих случаях путь возрастает со временем.
Вопросы для самопроверки студента
1. Графики х ( t ) для двух тел параллельны. Что можно сказать о скорости этих тел?
2. Графики l ( t ) для двух тел пересекаются. Обозначает ли точка пересечения графиков момент встречи этих тел?
Контрольные задания №2
Опишите движения, графики которых приведены на рис. 6. Запишите для каждого движения формулу зависимости x ( f ).
По графикам скорости (рис. 7) запишите формулы и постройте графики зависимости s x ( t ).
По приведенным на рисунке графикам скорости (см. рис. 8) запишите формулы и постройте графики зависимости s x ( t ).
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ. СКОРОСТЬ ПРИ НЕРАВНОМЕРНОМ ДВИЖЕНИИ. УСКОРЕНИЕ
1. Неравномерное движение. Из повседневной жизни известно, что равномерное движение встречается редко. Чаще приходится сталкиваться с движением, при котором скорость с течением времени меняется. Такое движение называют неравномерным.
2. Средняя скорость. Так как скорость при неравномерном движении изменяется во времени, то формулой 
3. Средняя путевая скорость. Однако средняя скорость не всегда подходит для описания движения. Рассмотрим такой пример: автомобиль выехал из гаража и через 2 часа вернулся обратно. Спидометр показывает, что автомобиль проехал 100 км. Какова средняя скорость движения?
Правильный ответ: средняя скорость равна нулю, потому что тело вернулось в начальную точку, т. е. перемещение тела равно нулю. Возможен и другой ответ, если определять не среднюю скорость, а среднюю путевую скорость, равную отношению пути, пройденному телом, ко времени движения: 
Знание средней скорости не дает возможности определять положение тела в любой момент времени, даже если известна траектория его движения. Однако это понятие удобно для выполнения некоторых расчетов, например, времени движения.
4. Примеры решения задач.
Вопросы для самопроверки студента
Почему нельзя говорить о средней скорости переменного движения вообще, а можно говорить только о средней скорости за данный промежуток времени или о средней скорости на данном участке пути?
Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?
Автомобиль за час проехал по прямому шоссе 60 км, а за следующий час — 30 км назад. Какова средняя путевая скорость на всем пути? Средняя скорость?
Задачи для самопроверки
Человек прошел по прямой дороге 3 км за 1 ч, потом повернул под прямым углом и прошел еще 4 км за 1 ч. Найдите среднюю и среднюю путевую скорости движения на первом этапе движения, на втором этапе и за все время движения. (Ответ: средняя скорость — 3 км/ч; 4 км/ч; 2,5 км/ч; средняя путевая скорость 3 км/ч; 4 км/ч; 3,5 км/ч.)
Человек проехал первую половину пути на автомобиле со скоростью 75 км/ч, а вторую половину — на велосипеде со скоростью 25 км/ч. Какова средняя путевая скорость на всем пути? (Ответ: 37,5 км/ч.)
Пешеход две трети времени своего движения шел со скоростью 3 км/ч. Оставшееся время — со скоростью 6 км/ч. Определите среднюю и среднюю путевую скорости движения пешехода. (Ответ: 4 км/ч.)
Для конспекта студента
■ Средняя скорость движения 

■ Средняя скорость — векторная величина.
■ Средняя путевая скорость равна отношению пути, пройденного телом, ко времени движения:
■ Средняя путевая скорость — скалярная величина.
Контрольные задания №3
1) Велосипедист проехал 80 км со скоростью 20 км/ч, а потом еще 60 км со скоростью 10 км/ч. Какова средняя путевая скорость его движения на всем пути?
2) Мотоциклист проехал 20 км за 30 мин, а затем ехал со скоростью 60 км/ч в течение 1,5 ч. какой была его средняя путевая скорость на всем пути?
3) Мотоциклист ехал сначала со скоростью 90 км/ч, а затем — со скоростью 30 км/ч. Какова средняя путевая скорость мотоциклиста на всем пути? Рассмотрите случаи, когда мотоциклист ехал со скоростью 90 км/ч: а) половину пути; б) половину времени.
ПРЯМОЛИНЕЙНОЕ РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ. УСКОРЕНИЕ
Мгновенная скорость. Если скорость тела изменяется со временем, для описания движения нужно знать, чему равна скорость тела в данный момент времени (или в данной точке траектории). Эта скорость называется мгновенной скоростью.
Можно также сказать, что мгновенная скорость — это средняя скорость за очень малый интервал времени. При движении с переменной скоростью средняя скорость, измеренная за различные интервалы времени, будет разной. Однако, если при измерении средней скорости брать все меньшие и меньшие интервалы времени, значение средней скорости будет стремиться к некоторому определенному значению. Это и есть мгновенная скорость в данный момент времени. В дальнейшем, говоря о скорости тела, мы будем иметь в виду его мгновенную скорость.
Ускорение. При неравномерном движении мгновенная скорость тела — величина переменная; она различна по модулю и (или) по направлению в разные моменты времени и в разных точках траектории. Все спидометры автомобилей и мотоциклов показывают только модуль мгновенной скорости.
Если мгновенная скорость неравномерного движения изменяется неодинаково за одинаковые промежутки времени, то рассчитать ее очень трудно. Такие сложные неравномерные движения нами не изучаются, поэтому рассмотрим только самое простое неравномерное движение — равноускоренное прямолинейное.
Прямолинейное движение, при котором мгновенная скорость за любые равные интервалы времени изменяется одинаково, называется равноускоренным прямолинейным движением.
Если скорость тела при движении изменяется, возникает вопрос: какова скорость изменения скорости? Эта величина, называемая ускорением, играет важнейшую роль во всей механике: ускорение тела определяется действующими на это тело силами.
Ускорением 
Термин «ускорение» используется в физике, когда речь идет о любом изменении скорости,— в том числе и тогда, когда модуль скорости уменьшается или когда модуль скорости остается неизменным и скорость изменяется только по направлению.
Скорость при прямолинейном равноускоренном движении. Из определения ускорения 

Таким образом, при прямолинейном равноускоренном движении проекция скорости линейно зависит от времени. Это означает, что графиком зависимости v x ( t ) является отрезок прямой.
График скорости разгоняющегося автомобиля дан на рис. 1.
График скорости тормозящего автомобиля дан на рис. 2.

Вопросы для самопроверки
Чему равна мгновенная скорость камня, брошенного вертикально вверх, в верхней точке траектории?
О какой скорости — средней или мгновенной — идет речь в следующих случаях:
поезд прошел путь между станциями со скоростью 70 км/ч;
скорость движения молотка при ударе равна 5 м/с;
скоростемер на электровозе показывает 60 км/ч;
пуля вылетает из винтовки со скоростью 600 м/с?
Два поезда идут навстречу друг другу: один — ускоренно на север, другой — замедленно на юг. Как направлены ускорения поездов?
Контрольные задания №4
Чему равна проекция ускорения, если в моменты времени t 1= 10 с и t 2 = 30 с проекции скорости v 1 x = 30 м/с и v 2 x =10 м/с? Начертите график v x ( t ).
Поезд через 10 с после начала движения прцобретает скорость 0,6 м/с. Через сколько времени от начала движения скорость поезда станет равной 3 м/с?
Для конспекта студента
■ Мгновенной скоростью называется скорость тела в данный момент времени (или в данной точке траектории).
■ Ускорением тела 
■ Прямолинейным равноускоренным движением называется движение тела вдоль прямой с постоянным ускорением. При прямолинейном равноускоренном движении скорость тела за любые равные интервалы времени изменяется на одну и ту же величину.
Уравнение скорости: 
ПЕРЕМЕЩЕНИЕ ПРИ ПРЯМОЛИНЕЙНОМ
РАВНОУСКОРЕННОМ ДВИЖЕНИИ
1. Перемещение при прямолинейном равноускоренном движении.
Для решения основной задачи механики нужно найти закон движения, определяющий положение тела в любой момент времени, т. е. s = f ( t ). Для этого нужно уметь находить вектор перемещения, а для нахождения перемещения, в свою очередь, удобно воспользоваться графическим методом.
Сначала следует всмнить, что при равномерном движении проекция перемещения s x численно равна площади фигуры, ограниченной графиком v x ( t ) и осью Ot .
Это справедливо и для неравномерного движения, потому что время движения можно разбить на такие малые интервалы времени, в течение каждого из которых движение тела можно считать практически равномерным (рис. 1).
Воспользуемся этим, чтобы найти зависимость перемещения от времени при прямолинейном равноускоренном движении.
Если начальная скорость тела равна нулю, фигура, ограниченная графиком v x ( t ) и осью Ot , — треугольник площадью a x t 2 /2 (рис. 2).
Следовательно, при прямолинейном равноускоренном движении без начальной скорости
Если начальная скорость тела не равна нулю, фигура, ограниченная графиком V x ( t ) и осью Ot , — трапеция, состоящая из прямоугольника площадью v Ox t и треугольника площадью a x t 2 /2 (рис. 3).
Таким образом, при прямолинейном равноускоренном движении с начальной скоростью
Средняя скорость при прямолинейном равноускоренном движении. Пользуясь выведенными выше формулами можно доказать, что

Соотношение между перемещением и скоростью. Для решения задач, в условии которых не задано время движения, полезны формулы, связывающие перемещение с начальной и конечной скоростями. Из формул
Если начальная скорость равна нулю, эта формула принимает вид:
Вопросы для самоконтроля
Когда модуль перемещения и пройденный путь совпадают?
Как связаны между собой проекции перемещения, модуль перемещения и пройденный путь при прямолинейном движении в одном направлении?
Как по графику скорости определить проекцию перемещения?
Контрольные задания №5
Уравнения движения различных тел, движущихся вдоль оси Ох, имеют вид (все величины измеряются в единицах СИ):
Автомобиль трогается с места и движется равноускоренно по прямому шоссе. За первую секунду автомобиль проходит 3 м. Какой путь пройдет автомобиль за первые 2 секунды? За первые 5 секунд?
Для конспекта студента
■ Проекция перемещения при движении без начальной скорости:
■ Проекция перемещения при движении с начальной скоростью:
■ Зависимость координаты от времени при движении с начальной скоростью:
■ Уравнение средней скорости:
■ Соотношение между перемещением и скоростью:
без начальной скорости: 
с начальной скоростью:
Контрольные задания №6
За первую секунду равноускоренного движения без начальной скорости тело прошло 5 м. Какое расстояние оно прошло за первые 3 с? За первые 10 с?
При прямолинейном равноускоренном движении за 10 с скорость тела уменьшилась с 20 м/с до 10 м/с. Каково перемещение тела за это время? Какова скорость через 5 с после начала наблюдения?
Тележка скатывается с наклонной плоскости равноускоренно. Пройдя расстояние 2 м, она приобретает скорость 1 м/с. Какое расстояние должна преодолеть тележка, чтобы приобрести скорость 2 м/с?
Пуля, летевшая со скоростью 400 м/с, пробила стену толщиной 20 см, в результате чего скорость пули уменьшилась до 100 м/с. Сколько времени двигалась пуля в стене?
СВОБОДНОЕ ПАДЕНИЕ ТЕЛ. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
1. Свободное падение. Ускорение свободного падения. Великий ученый древности Аристотель на основе наблюдений построил теорию, согласно которой чем тяжелее тело, тем быстрее оно падает. Эта теория просуществовала две тысячи лет — ведь камень действительно падает быстрее, чем цветок!
Возьмем два тела, легкое и тяжелое, свяжем их вместе и бросим с высоты. Если легкое тело всегда падает медленнее, чем тяжелое, оно должно «притормаживать» падение тяжелого тела, и поэтому связка двух тел должна падать медленнее, чем одно тяжелое тело. Но ведь связку можно считать одним телом, еще более тяжелым, и, значит, связка должна падать быстрее, чем одно тяжелое тело!
Обнаружив это противоречие, Галилей решил проверить на опыте, как же в действительности будут падать шары разного веса: пусть ответ на этот вопрос даст сама природа. Он изготовил два шара и сбросил их с Пизанской башни — оба шара упали почти одновременно!
Падение тела в условиях, когда сопротивлением воздуха можно пренебречь, называют свободным падением.
Тот факт, что свободное падение тел — ускоренное движение, не вызывает сомнений. В этом легко убеждиться, наблюдая за движением падающего шарика и других тел. Однако на вопрос, является ли свободное падение равноускоренным движением, трудно ответить. Ответ на этот вопрос может дать эксперимент. Если, например, сделать ряд моментальных снимков падающего шарика через равные промежутки времени (стробоскопические фотографии), то по расстояниям между последовательными положениями шарика можно определить, что движение действительно является равноускоренным.
Значит 
2. Зависимость скорости и координаты падающего тела от времени. Если совместить начало координат с начальным положением тела и направить ось Оу вниз, то графики v y ( t ) и y ( t ) будут иметь следующий вид (рис. 1).
Таким образом, при свободном падении скорость тела увеличивается за каждую секунду примерно на 10 м/с (рис. 2).
3. Зависимость скорости и координаты тела, брошенного вертикально вверх, от времени. Далее следует рассмотреть случай, когда тело брошено вверх. Если совместить начало координат с начальным положением тела и направить ось у вертикально вверх, то проекции скорости и перемещения в начале движения будут положительными.
На рисунках 3, 4 приведены графики v y ( t ) и y ( t ) для тела, брошенного вертикально вверх с начальной скоростью 30 м/с.
4. Связь начальной скорости бросания и конечной скорости падения.
Далее можно сравнить уравнения для скоростей свободно падающего тела: v y = v Oy + gt и тела, брошенного вертикально вверх, v y = v Oy — gt .
Вопросы для самопроверки
Одинаковым ли будет время свободного падения различных тел с одной и той же высоты?
Чему равно ускорение тела, брошенного вертикально вверх, в верхней точке траектории?
Из одной точки падают без начальной скорости два тела с интервалом времени t секунд. Как движутся эти тела относительно друг друга в полете?
Контрольные задания №7
1. Тело свободно падает без начальной скорости. Какое расстояние оно • пролетает за первую секунду? За вторую секунду? За третью секунду?
2. Камень падал с одной скалы 2 с, а с другой 6 с. Во сколько раз вторая скала выше первой?
Для конспекта студента
■ Свободным падением называется падение тела в условиях, когда сопротивлением воздуха можно пренебречь.
■ Зависимость скорости от времени при движении с начальной скоростью:

РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
Особенности криволинейного движения. Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любое криволинейное движение можно рассматривать как движение по дугам окружностей с различными радиусами. Изучение движения по окружности дает также ключ к рассмотрению произвольного криволинейного движения.
Далее перейдем непосредственно к рассмотрению равномерного движения по окружности, т. е. движения по окружности с постоянной по модулю скоростью.
Основные характеристики равномерного движения по окружности. Период обращения Т — это время одного полного оборота.
Чтобы совершить один полный оборот, тело должно пройти путь 2π r (длина окружности). Следовательно,
Частота обращения «ύ» равна числу полных оборотов за единицу времени.
Угловая скорость ώ =
где — угол поворота радиуса, проведенного к телу из центра окружности, по которой движется тело за время (рис. 1).
При криволинейном движении мгновенная скорость в любой точке траектории направлена по касательной к траектории в этой точке. А поскольку касательная к окружности перпендикулярна радиусу, то мгновенная скорость при движении по окружности в каждой точке траектории направлена перпендикулярно радиусу (рис. 2). 
Ускорение при равномерном движении по окружности. При движении по окружности, как и при любом криволинейном движении, направление скорости изменяется со временем. А раз скорость тела изменяется — хотя бы только по направлению,— значит, тело движется с ускорением. При равномерном движении изменение скорости обусловлено только изменением направления скорости. Нетрудно доказать, что изменение скорости 
Ускорение 

Рассмотрим равнобедренный треугольник, образованный векторами v 1, v 2 и 


Контрольные вопросы №1
1. Как направлена мгновенная скорость при движении по окружности?
2. Как направлено ускорение при равномерном движении по окружности?
3. Можно ли равномерное движение по окружности считать равноускоренным движением?
При равномерном движении по прямой ускорение равно нулю. Можно ли равномерное движение по кривой считать движением без ускорения?
Два тела движутся по окружностям разных радиусов. Ускорение какого тела больше, если: а) скорости тел одинаковы; б) периоды обращения тел одинаковы?
Контрольные задания №9
1. Во сколько раз скорость конца минутной стрелки башенных часов больше скорости конца минутной стрелки наручных часов, если длина стрелки башенных часов 1,5 м, а длина стрелки наручных часов 1,5 см?
2. С каким ускорением движется автомобиль по кольцевой трассе, имеющей вид окружности радиусом 100 м, если скорость автомобиля 20 м/с? Во сколько раз это ускорение меньше ускорения свободного падения?
Для конспекта ученика
■ Равномерным движением по окружности называется движение по окружности с постоянной по модулю скоростью.
■ Мгновенная скорость в данной точке траектории направлена по касательной к траектории в этой точке, т. е. перпендикулярно радиусу, проведенному из центра окружности в данную точку.
■ При равномерном движении по окружности ускорение в каждый момент времени направлено по радиусу к центру окружности. Модуль центростремительного ускорения можно найти по любой из формул:
Составить конспект по лекции.
Ответить на контрольные вопросы.
Решить контрольные задачи.
Предоставить выполненные задания на электронный адрес:
Срок выполнения задания до 21.10.2020 г.