Два автомобиля, обладающие полезными мощностями N1 и N2, развивают скорости v1 и v2 соответственно. Какую скорость
Ответы
ответ к заданию по физике
солнечьная, термальная(геотермальная), энергия приливов(отливов), биотоплево. примеры не могу сори.
диагноз дифтонг догнать дольщик дорожка дочиста дружина дурашка дыхание даровой девятка денежка десятью дивчина добавка дозатор домрист доспать драться дряблый духобор двойной деканат деревня детство динамит доверие долевой доплата досылка дремота дубовый душегуб далекий дебитор деловой дернина деятель джунгли дисплей догадка дольник дорогой дочерна дурачье дырявый дармоед девчата демпинг десятый дивизия дневной дожитие домосед досмотр драпать дрыгать дуршлаг двойник декабрь дергать детский динамик довезти долгота донжуан досужий дремать дубинка душевой дактиль дебелый делимое дерзить дешевый дискета довлеть дольний дорасти дохнуть дрожать дурачок дырокол дареный девушка демагог десяток джемпер диаметр дневник дождить домовый дослать дощечка дружный дурость двинуть действо депутат детская дилогия доброта долбить донести достичь дрезина дуализм душевая давалец двучлен деление дерзать дешевка дискант довести должный допьяна доучить дробный дуранда дымоход дантист девочка делянка десятка джейран диалект длиться доехать домовой досадка дощатый дружище дурнота двигать девятью депозит детеныш дилемма добреть доиться домысел достать древний дряхлый духовой двоякий делегат держать децибел дирижер довесок должник дополна дотемна дробить дуралей дуэлянт девичья дельфин десница джазист диадема длинный договор домкрат дортуар дощаник дружить дурнеть дьячиха датчане девятый денница детвора диктант добрать дозреть домчать доспехи дребезг дрянной духовка дворник декорум держава дефицит диорама доверху должать доплыть дотация дробина дубрава душечка дальний дебошир дельный дернуть деяться
Два автомобиля полезная мощность которых n1 и n2
Страницы работы
Содержание работы
Два
автомобиля, полезные мощности которых N1 = 40 кВт
и N2 = 60 кВт, развивают скорости υ1 = 20 км/чи υ2 = 120 км/ч соответственно. Какую
скорость υ они разовьют, если сцепить их вместе?
Малый
поршень гидравлического пресса за один ход опускается на высоту h = 0,2 м, а большой поршень поднимается на высоту H = 0,01 м. С какой силой действует пресс на зажатое в нем
тело, если на малый поршень действует сила f = 400
H?
Поезд
массы m=1500 т движется со скоростью v=54 км/ч
и при торможении останавливается, пройдя путь s = 200
м. Какова средняя сила торможения F?
К
концам стержня массой m = 1 кг и длиной L = 1 м
подвешены грузы m1 = 1 кг
и m2 = 3 кг.
На каком расстоянии от точки подвеса большего груза должна располагаться
точка опоры, чтобы стержень находился в равновесии?
На
двух концевых опорах лежит балка длиной 2 м, к которой подвешен груз массой m
на расстоянии 0,5 м от левого конца. Если масса груза в два раза меньше массы
балки, то сила, действующая на левую опору равна
Если
автомобиль массы m, трогаясь с места и двигаясь равноускоренно,
проходит путь S за время t, то
двигатель автомобиля в конце пути развивает мощность
Пуля,
летящая со скоростью 600 м/с, пробивает несколько одинаковых расположенных
друг за другом досок. В какой по счёту доске застрянет пуля, если её скорость
после прохождения первой доски равна 500 м/с?
В
сообщающихся сосудах одинакового диаметра находится ртуть. Когда в правую
трубку наливают керосин, высота столба которого 34 см, уровень ртути в левой
трубке поднимается на 1 см. Определить плотность керосина. Плотность ртути ρрт
= 13,6·103 кг/м3.
Объём
железного шарика 100 см3. Какую силу необходимо приложить, чтобы
удержать его полностью погруженным в воде во взвешенном состоянии? Плотность
железа ρж=7,8·103 кг/м3, плотность воды ρв=
103 кг/м3
Однородная
балка массой m = 120 кг упирается одним концом в угол между стеной и полом.
Угол наклона
По
доске, наклоненной к горизонту под углом α = 30°, можно передвигать вверх или
вниз грузы, прикладывая силу вдоль доски. Чтобы передвинуть ящик массой m =
30 кг вниз на расстояние L = 3 м, надо совершить минимальную работу А = 100
Дж. Найдите коэффициент трения между ящиком и доской.
По
доске, наклоненной к горизонту под углом α = 30°, можно передвигать вверх или
вниз грузы, прикладывая силу вдоль доски. Чтобы передвинуть ящик массой m =
30 кг вверх на расстояние L = 3 м, надо совершить минимальную работу А = 1000
Дж. Найдите коэффициент трения между ящиком и доской.
Какая
работа произведена при сжатии буферной пружины железнодорожного вагона на l1 = 5 см,
если для сжатия пружины на l2 = 1 см
требуется сила F = 30 кН?
Под
действием постоянной горизонтальной силы F тело
массы 5 кг движется с ускорением 1 м/с2.
Коэффициент трения между телом и плоскостью 0,1. Какую работу совершит сила F
когда тело пройдет путь 10 м?
Под
действием постоянной горизонтальной силы тело массы 5 кг движется с
ускорением 1 м/с2. Коэффициент трения между телом и
плоскостью 0,1. Какую работу совершит сила трения когда тело пройдет путь 10
м?
Однородная
балка массы 30 кг одним концом лежит на опоре, другой конец её удерживается
канатом АВ в
На
невесомой балке находятся два груза массы 10 кг каждый. Расстояние между
опорами балки 4 м. Найдите
Однородный
стержень массы 600 г одним концом опирается о пол, а другой его конец
удерживается нитью АВ
Пуля,
летящая с некоторой скоростью горизонтально, углубляется в стенку на расстояние
l1 = 16
см. Если пренебречь зависимостью между силой сопротивления среды и скоростью
в ней, то пуля, которая будет иметь скорость вдвое меньшую углубится в ту же
стенку на расстояние …(см)
В
цилиндрический сосуд с площадью дна 30 см2 налито масло с
плотностью 800 кг/м3. Если в этот сосуд опустить маленький
шарик массы 48 г, плотность которого 600 кг/м3, то уровень
масла поднимется на … см.
На
поверхности жидкости плавает шар объема 18 см3. Внутри шара
есть полость объема 16 см3. Если плотность жидкости в 3 раза
меньше плотности вещества шара, то объем погруженной в жидкость части шара
равен … см3.
Санки
массой m = 8 кг скатились с горы высотой h = 5 м и остановились на
горизонтальном участке. Какую минимальную работу (в Дж) совершит мальчик,
возвращая санки по линии их скатывания?
Однородный
стержень одним концом опирается о пол, а другой его конец удерживается нитью
АВ как показано
Груз
массы 2 кг равномерно втаскивают по наклонной плоскости на высоту
5 м. На этой высоте груз срывается, и начинает скользить вдоль наклонной
плоскости. Если на подъем груза была затрачена работа 175 Дж, то у
основания наклонной плоскости он будет иметь скорость
Тело
всплывает в жидкости с глубины h без начальной скорости.
Плотность тела в два раза меньше плотности жидкости. Если средняя сила
сопротивления движению в четыре раза меньше силы тяжести, то время, за
которое тело всплывет, равно
На
двух вертикальных пружинах жесткости k1 = 0,1 Н/м и k2 = 0,2 Н/м подвешен за концы стержень длиной
1 м и массой 4 кг. Если пружины в недеформированном состоянии имеют
одинаковую длину, то для того чтобы стержень принял горизонтальное положение,
к нему нужно подвесить груз массой 5 кг на расстоянии … см от пружины
жесткости k1,
Ртуть
находится в сообщающихся сосудах. Площадь сечения левого колена в 3 раза
меньше, чем правого. Уровень ртути расположен на расстоянии 30 см от верхнего
конца трубки. На сколько поднимется уровень ртути в правом колене (в см),
если левый медленно доверху залить водой? Плотность ртути ρрт =
13,6·103 кг/м3, плотность воды ρв = 103
кг/м3
Похожие материалы
Информация о работе
Задания на контрольные работы
более месяца назад
Просмотров : 22
Ответов : 1
Лучший ответ:
более месяца назад
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт
Лучшее из галереи за : неделю месяц все время
Два автомобиля полезная мощность которых n1 и n2 развивают скорости
9. Законы сохранения. Работа, мощность, энергия.
1. От чего зависит работа силы тяжести?
2. Чему равна работа силы тяжести при горизонтальном движении? при движении тела по замкнутой траектории?
3. Тело свободно падает с некоторой высоты. Одинаковую ли работу совершает сила тяжести за одинаковые промежутки времени?
4. Зависит ли работа силы упругости от формы траектории?
5. В чем сходство работ, совершаемых силой упругости и силой тяжести?
6. Две одинаковые пружины (железная и медная) упруго растянуты: а) на одинаковую длину; б) одинаковыми силами. На растяжение какой пружины надо затратить большую работу в этих случаях?
7.Всегда ли работа силы трения скольжения отрицательна? Может ли работа силы трения скольжения быть равной нулю? Может ли совершать работу сила трения покоя?
8. Тело массой m поднимают на высоту h: а) вертикально вверх; б) по гладкой наклонной плоскости; в) по шероховатой наклонной плоскости. Сравните работы внешней силы и силы тяжести.
9. Столб длиной l и массой m, лежащий на земле, устанавливают вертикально. Какая при этом совершается работа?
10. Лифт массой 300 кг поднимается на 10 м. Какую работу совершит сила натяжения каната, поднимающего лифт? Какую работу совершит сила тяжести? [29 k ; –29 k ]
11. Представим, что к центру Земли прорыли шахту. Какую работу надо совершить, чтобы вытащить тело массой 1 кг из центра на поверхность? [31 M]
12. Груз массой 50 кг свободно падает из состояния покоя в течение 10 с. Какую работу совершает сила тяжести за это время? [250 k ]
13. Вагонетку с рудой массой 300 кг поднимают равномерно по наклонной эстакаде длиной 20 м и высотой 5 м. Коэффициент трения 0,05. Найти работу силы трения и работу силы тяжести. [–2,9 k ; –15 k ]
14. Жесткость пружины k, длина lо. Определить работу, которую надо совершить, чтобы растянуть пружину до длины l?
15. Какая работа произведена при сжатии буферной пружины на 3 см, если для сжатия ее на 1 см требуется сила 35 кН? [1575]
16. Пластинка массой m лежит на горизонтальном столе. В центре пластинки укреплена легкая пружина с жесткостью k. Какую работу надо совершить, чтобы на пружине равномерно поднять пластинку на высоту h от поверхности стола? [(mg) 2 /2k + mgh]
17. Из шахты глубиной 200 м равномерно поднимают груз массой 500 кг на канате, масса каждого метра которого равна 1,5 кг. Какая при этом совершается работа? [1300]
18. Пружина жесткостью 1 кН/м была сжата на 4 см. Какую работу надо совершить, чтобы увеличить сжатие до 18 см? [ 15,4 ]
19. Тело массой 5 кг движется под действием силы, равной 30 Н, направленной под углом 30 о к горизонту. Определить скорость тела через 10 c от начала движения и работу против силы трения, если коэффициент трения скольжения равен 0,2. [ 38; 1330]
20. К лежащему на горизонтальной поверхности бруску массой 12 кг прикреплена пружина жесткостью 300 Н/м. Коэффициент трения 0,4. К свободному концу пружины приложена сила под углом 30 о к горизонту, под действием которой груз равномерно перемещается на расстояние 4 м. Определить совершенную работу. [ 1 59]
22. Какую работу надо совершить, чтобы вывести спутник массой 500 кг на круговую орбиту, проходящую вблизи поверхности Земли? Сопротивление воздуха не учитывать. [15,7 Г]
23. Определить кинетическую энергию тела массой 1 кг, брошенного горизонтально со скоростью 20 м/с, в конце четвертой секунды его движения. [970]
24. Тело, брошенное вертикально вверх, упало обратно через 4 с после начала движения. Определить кинетическую энергию в момент падения и потенциальную энергию в верхней точке, если масса тела 200 г. [38]
25. По канатной железой дороге, идущей с углом наклона 45 о к горизонту, поднимается вагонетка массой 500 кг. Найти работу, которую совершает мотор подъемника, при поднятии вагонетки на высоту 10 м. Коэффициент трения принять m = 0,1. [54000]
26. Тележка движется по горизонтальной дороге со скоростью 18 км/ч и въезжает на подъем. На какой высоте над уровнем дороги остановится тележка? [1,28]
27. На нити длиной l подвешен шар. Какую горизонтальную скорость нужно сообщить шару, чтобы он отклонился до высоты точки подвеса? [(2gl) 1/2 ]
28. Пружина жесткостью k = 100 кН/м и массой m = 400 г падает на землю с высоты h = 5 м. На сколько сожмется пружина, если при ударе ее ось остается вертикальной? [20 м]
31. Найти полезную мощность двигателя мотодельтаплана, имеющего полетную массу 200 кг, при горизонтальном полете со скоростью 72 км/ч. Известно, что отношение подъемной силы к силе лобового сопротивления k = 5, а КПД винтомоторной установки 0,4. [20000]
33. Почему расходуется больше бензина в случае, когда автомобиль движется с ускорением, чем при движении с постоянной скоростью?
35. Тело массой 100 г, брошенное вертикально вниз с высоты 20 м со скоростью 10 м/с, упало на землю со скоростью 20 м/с. Найти работу по преодолению сопротивления воздуха. [4,6]
36. Когда к пружине подвешен груз массой 3 кг, ее длина 112 мм. Если масса груза 8 кг, то длина пружины 132 мм. Какую работу необходимо совершить, чтобы растянуть пружину из недеформированного состояния до длины 132 мм? [ 1,25 ]
37. Две пружины, жесткости которых раны 300 Н/м и 500 Н/м, скреплены последовательно и растянуты так, что растяжение второй пружины 3 см. вычислите работу по растяжению пружин.
38. На горизонтальной плоскости лежит брусок массой 2 кг. К бруску, прикреплена пружина жесткостью 100 Н/м, к пружине приложили горизонтально действующую силу. Какую работу, совершит сила к моменту, когда брусок начинает скользить? Коэффициент трения о плоскость 0,5.
39. Тормозной путь автомобиля, двигавшегося горизонтально со скоростью 30 км/ч, равен 7,2 м. Чему будет равен тормозной путь, если его скорость увеличится до 50 км/ч? [ 20 ]
40. Санки массой 2 кг и длиной 1 м выезжают со льда на асфальт. Коэффициент трения полозьев об асфальт 0,5. Какую работу, совершит сила трения к моменту, когда санки полностью окажутся на асфальте? [ –5 ]
41. Для того чтобы вытащить целую пробку из бутылки, нужно совершить работу 2 Дж. Какую работу нужно совершить, чтобы откупорить бутылку, у которой отломалась и выкрошилась верхняя половина пробки? Пробку считать невесомой. [1,5]
43. Если автомобиль въезжает на гору при неизменной мощности двигателя, то водитель уменьшает скорость движения. Почему?
44. Автомобиль массой 2 т трогается с места и движется в гору, уклон которой 0,02. Пройдя расстояние 100 м, он развивает скорость 9 м/с. Коэффициент трения 0,05. Определить среднюю мощность, развиваемую мотором автомобиля. [9944]
46. Мощность гидроэлектростанции N = 73,5 МВт, коэффициент полезного действия 0,75. Определить на какой уровень плотина поднимает воду, если расход воды 1 × 10 3 м 3 /с. [10]
47. Найти мощность воздушного потока, имеющего поперечное сечение в виде круга диаметром d = 18 м и движущегося со скоростью 12 м/с. [280 k ]
49. С ледяной горы высотой 1 м и основанием 5 м съезжают санки, которые останавливаются, пройдя горизонтальный путь 95 м. Найти коэффициент трения и КПД наклонной плоскости. [0,01; 95]
Смотрите новый сайт В. Грабцевича по физике, а также шутки про школу.
Максимальная скорость, аэродинамика, мощность и момент (мат. часть)
Доброго времени суток, в прошлой записи Максималки Astra G на которую меня сподвигло большое количество сказочников я пропустил мимо практически всю физику. Видимо зря. Не то, чтобы меня это сильно беспокоило, но ввиду свободного времени в выходной и плохой погоды — решил состряпать статейку из нескольких копи-паст (источники вконце) и немножко отсебятины.
Всем остальным для общего развития не помешает почитать и подчерпнуть какие-то знания, или уточнить что-то, что вызывало сомнения. Возможно пригодится кому-то, чтобы объяснить своему товарищу, что » вы, батенька, пиздите » он не прав и немножко привирает. Потому что, даже грамотные и уважаемые люди после прошлой записи немного недопонимали основного. Цитата » Тебя сейчас бомбанет если я напишу что мой нексиевский 8миклоп с длинным коробасом 200 поедет, только скорость буду набирать примерно минут 20» Не бомбануло, он поедет столько-же сколько и с «коротким коробасом», почему? читаем про мощность и момент.
Часть 1. Коэффициент аэродинамического сопротивления Cx
Наверное, каждый слышал о том, что сила сопротивления воздуха пропорциональна квадрату скорости – столь быстро нарастает противодействие движению в процессе разгона. Впечатляет, но как это соотнести с параметрами автомобиля? Для этого нужно лишь перейти в термины механической работы, и тогда получится, что отбираемая от двигателя мощность находится аж в кубической зависимости от скорости! Только представьте, с каким трудом даются автомобилю последние десятки километров в час. В таких условиях даже значительная прибавка мощности мотора не в состоянии существенно увеличить максимальную скорость.
Таким образом, задача снижения лобового сопротивления – приоритетная задача не только для аэродинамики, но, в свете борьбы за экологию, и для всего автомобилестроения в целом.
Решение можно искать по двум направлениям. Первое – это уменьшение площади поперечного сечения автомобиля, иными словами, создание более узкого и низкого кузова. Путь весьма эффективный, ибо сопротивление воздуха напрямую зависит от размеров объекта, но, к сожалению, совершенно расходящийся с нынешней тенденцией к увеличению габаритов автомобилей. И увеличению, стоит отметить, немалому, ведь в моду активно входят кроссоверы, вторгающиеся даже в совершенно чуждый им сегмент спортивных, скоростных автомобилей, где требования к аэродинамике предельно высоки.
А значит остается второй и единственный вариант – оптимизация процесса обтекания кузова, критерием совершенства которого как раз и является коэффициент аэродинамического сопротивления Cx (или Cw, как иногда встречается в литературе).
Величина Cx определяется опытным путем. Факторов, влияющих на Cx автомобиля, несколько: во-первых, это внутреннее сопротивление, возникающее при прохождении воздуха через подкапотное пространство и салон, во-вторых, сопротивление трения между воздушным потоком и поверхностью кузова, и, в-третьих, сопротивление формы, проявляющееся главным образом в избыточном давлении перед автомобилем и разряжением позади него.
Внутреннее сопротивление составляет около 12% от общей величины, и пока особых успехов в этой области не наблюдается: напротив, все более и более мощные моторы современных автомобилей требуют все больше воздуха для охлаждения. Например, в пределе 300-сильный бензиновый двигатель выделяет в виде тепла около 450кВт – этого хватило бы для отопления нескольких особняков! Соответственно, растут размеры радиаторов, уплотняются моторные отсеки, увеличивается сопротивление воздуха… Существенные же улучшения здесь возможны лишь при переходе на более эффективные электродвигатели, но пока они так и остаются технологией будущего.
Сопротивление поверхностного трения так же вносит свой 10-процентный вклад в величину Cx. Вообще, наличие столь ощутимого трения между воздухом и кузовом может показаться странным, но оно действительно имеет место: прилегающий к поверхности слой воздуха сталкивается с микронеровностями покрытия и тормозиться — образуется так называемый пограничный слой. Пока это течение находится в ламинарном состоянии, то есть все его частицы движутся в одном направлении, толщина пограничного слоя невелика (около нескольких миллиметров) и сопротивление трения небольшое. Но с переходом в турбулентное состояние, когда поток «спотыкается» о более крупное препятствие, и траектории его частиц становятся хаотичными, пограничный слой расширяется, а вместе с ним увеличивается и трение – воздух словно становится более вязким. Таким образом, от разработчиков в данном случае требуется обеспечение гладкости кузова, дабы пограничный слой дольше оставался ламинарым. А для этого нужно уменьшать зазоры кузовных элементов, закрывать уплотнителями щели между деталями. Помогает и придание поверхностям небольшой кривизны – прилегающий поток ускоряется, давление в нем падает, и траектории частиц упорядочиваются. К сожалению, в целях экономии этими мерами в последнее время частично пренебрегают, например, уплотнители по периметру лобового стекла или вокруг фар сейчас встретишь нечасто.
И, наконец, сопротивление формы или сопротивление давления – главный фактор, определяющий значение Cx. Причина его возникновения понятна – спереди на автомобиль давит набегающий поток воздуха, а позади его «оттягивает» назад зона разряжения, образующаяся в результате отрыва потока от резко заканчивающегося кузова. Решение проблемы тоже, казалось бы, очевидно – нужно придать автомобилю такую форму, чтобы он плавно рассекал воздух и опять-таки плавно, без отрыва потока от поверхности, позволял ему сойтись позади себя. Но загвоздка в том, что в соответствии с такими требованиями автомобиль должен напоминать дирижабль (точнее, его половину, отрезанную в продольной плоскости), то есть иметь минимум граней и, главное, очень длинную, постепенно сужающуюся заднюю часть. Разумеется, о рациональной компоновке в данном случае говорить трудно.
Немножко о Cx ВАЗов.
Что может стандартный ВАЗовский двигатель и чего он не может.
Скоростные характеристики.
ВАЗ 2108-09-99-2115: Cx — 0,468; S (площадь лобового сопротивления) — 1,8
1100 карб. (39,7 кВт/54,4 л.с.) — 139, 35 км/ч.
1300 карб. (47 кВт/64,4 л.с.) — 147,42 км/ч.
1500 карб. (51,5 кВт/71,6 л.с.) — 152 км/ч.
1500 инж. (60 кВт/82,2 л.с) — 159,92 км/ч.
ВАЗ 2110: Cx — 0,348; S (площадь лобового сопротивления) — 1,93
1500 инж. 8-кл. (56 кВт/76,7 л.с.) — 168,54 км/ч.
1500 инж. 16-кл. (69 кВт/94,5 л.с.) — 180,69 км/ч
Для достижения «зубилом» скоростного барьера в 200 км/ч. необходима мощность двигателя 160 л.с, «десятке» потребуется поменьше — 130 л.с. Другие «контрольные точки» —
170 км/ч — 100 л.с (2108)/ 80 л.с (2110)
180 км/ч — 120 л.с (2108)/ 95 л.с (2110)
190 км/ч — 140 л.с (2108)/110 л.с (2110)
Будьте реалистами. Законы физики обмануть невозможно. Для преодоления каждых «лишних» 10 км/ч на максимальных скоростях «зубилкам» требуется около 20 л.с, «матрешкам» — 15 (Дальше — еще больше: сопротивление растет пропорционально квадрату скорости) Хвастливые утверждения о достижении на стандартных авто ВАЗ скорости 200 (300) км/ч. могут вызвать лишь улыбку. Cx Нивы 0.536 поэтому я дико ржал с мифического родственника одного из коментаторов, который 170 на ней ехал. 137 максималка НИВЫ.
Барьер 300 км/час требует от двигателя минимум 390 лошадиных сил и двигаться на таких скоростях могут только спортивные авто либо седаны огромной по 600+лс мощности.
400 км/час. Даже имея двигатель мощностью 1000 лошадиных сил не каждый суперкар может развить эту скорость ведь сопротивление воздуха на таких скоростях так велико что для преодоления каждых 10 км/час приходиться добавлять к мощности двигателя около 100 лошадей.
Часть 2. Мощность и крутящий момент
Часто эксперты автомобильных изданий, рассказывая о выдающейся динамике машины, в первую очередь превозносит огромный крутящий момент двигателя, оставляя мощности роль второго плана. Мол, благодаря именно моменту машина ровно и напористо разгоняется в широком диапазоне оборотов и скоростей. Особенно востребовано это качество на высших передачах, – ведь тяговые силы и ускорения на них в любом случае не столь велики, как на первой или второй передаче. А для безаварийного движения в потоке транспорта возможность быстро прибавить скорость зачастую играет судьбоносную роль. Ездить на таком автомобиле даже психологически легче. И все же, когда нужно быстрей разогнаться, что важней – мощность или крутящий момент?
Сразу отметим: чаще всего эти два параметра «конфликтуют»… в головах журналистов, охотно повторяющих признанные публикой «истины» без какого-либо их анализа. На самом же деле смешно рассматривать мощность в отрыве от крутящего момента и наоборот. Первая показывает энергию, ежесекундно вырабатываемую двигателем, тогда как крутящий момент – всего лишь силовой фактор, показывающий, как нагружен при работе коленчатый вал.
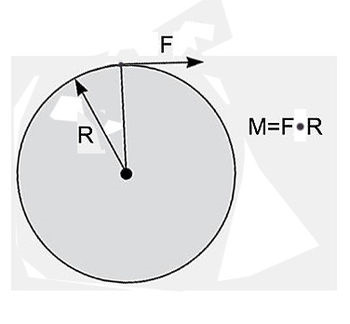
Тут впору вспомнить школьную физику. Нарисуйте круг радиуса R – это будет сечение вала – и приложите к нему «касательную» силу F.
Крутящий момент этой силы М = F • R. За один оборот вала сила F пройдет путь 2πR – и выполнит работу: А = F • R • 2π = М • 2π. А работа за n оборотов: А = М • 2π • n. Если n – число оборотов в минуту, то работа за одну секунду – то есть, мощность – составит N = М • 2πn /60.
Выражение 2π n /60 = 0,1047 n = ω – угловая скорость вала. Итак, N = М • 0,1047 n (Формула [1]).
Но мы имеем дело не только с вращающимися деталями, но и движущимися линейно. В этом случае в формуле (1) момент М заменим силой F, а угловую скорость ω – линейной v. Получим: N = F • v (Формула [2]).
Эти формулы равноправны. Замерив, например, тяговую силу колес, умножим на достигнутую машиной скорость – и найдем затрачиваемую мощность. Но если крутящий момент на ведущей оси умножить на угловую скорость колес, получим то же самое.
Итак, мощность – это работа (или энергия) израсходованная или произведенная за 1 секунду. Конечно, о «законе сохранения энергии» знает каждый. Говоря по пионерски, она «не возникает из ничего», но и не исчезает, не оставив следа. Так, лишь около четверти тепловой энергии, получаемой двигателем от сгорания топлива, превращается в механическую, соответствующая мощность (эффективная) тратится на движение машины. Большая же часть полученной в цилиндрах двигателя теплоты идет на «обогрев» окружающего нас мира.
Эффективная мощность тоже доходит до ведущих колес не вся – до 15 % ее может рассеять в виде тепла трение в узлах и агрегатах трансмиссии. Но для нас важней другое: если при открытом дросселе (или при полной подаче топлива в дизель) двигатель выдает на колеса сколько-то киловатт, то это – его «потолок». Никакими простыми механизмами вроде коробок передач, редукторов и т. п. превысить эту величину невозможно – этого «закон сохранения» не допустит.
Итак, крутящий момент – это удобный для нас «инструмент», связывающий процессы в двигателе с трансмиссией машины и ведущими колесами. Но не более того
Из формулы (1) видно, что для получения достаточной мощности вовсе не обязателен огромный крутящий момент, ведь в произведении два сомножителя. Почему бы, например, не увеличивать мощность при постоянном моменте, наращивая угловую скорость в каком-то диапазоне оборотов? При этом мощность растет по оборотам линейно. А постоянство момента в заданном диапазоне – не чудо, которым некоторые почему-то восторгаются, а всего лишь признак постоянства тяговых сил. Если пренебречь сопротивлением воздуха (к примеру, на первой передаче оно невелико), то и ускорение машины в этом диапазоне постоянное. Это довольно удобно для водителя. Но спросим себя: если бы в начале диапазона момент был таким же, а ближе к пресловутым «верхам» стал больше, стал бы с таким «подхватом» автомобиль хуже? – Вряд ли. Разве только что-нибудь нарушилось бы в смысле экологии.
Мощность можно менять и при постоянных оборотах. Пример: мы ехали со скоростью 90 км/ч по горизонтальному шоссе, а с началом подъема, дабы сохранить скорость, пришлось больше открыть дроссель. Это увеличение момента в чистом виде.
Если пренебречь разницей в КПД передач (она невелика), то на любой передаче машину движут одни и те же киловатты. Но движут по-разному. Момент и тяговая сила на ведущих колесах подчиняются «золотому правилу»: сколько процентов выиграешь в скорости, столько потеряешь в силе. Это показывают рис. 1 и 2. Если двигатель заведомо слаб, с ним сильно не разгонишься.
Величины мощности N1 … N5 на ведущей оси не зависят от включенной передачи. Точки пересечения кривой Nсопр с кривыми N3, N4 и N5 дают информацию о максимальных скоростях автомобиля на этих передачах. Здесь самая скоростная на горизонтальной дороге в безветрие – четвертая.
Главные враги любителя скорости – не гаишники, а силы, тормозящие движение, – от этих не откупишься! Мощность сопротивления воздуха вкупе с мощностью шинных потерь показаны на рис. 1 линией Nсопр.
(Желающие посчитать, могут воспользоваться следующими формулами. Nсопр. = Nw + Nf. Мощность аэродинамических потерь Nw для автомобиля весом 15000 Н при плотности воздуха 1,25 кг/м3, Сх = 0,3 и лобовой площади S = 2 • м2 составляет: Nw = (0,3 • 2 • 1,25)/2 • v3 = 0,375 v3 Вт. А мощность шинных потерь Nf = 0,015 • 15000 • v = 225 v Вт. При 100 км/ч Nсопр составляет лишь 14,5 кВт. А при 200 км/ч – 77 кВт. Разница впечатляет?)
Колеса автомобиля, борясь с мощностями сил сопротивления, при максимальной скорости полностью расходуют мощность, получаемую от двигателя. Но ее характеристика (например, показанная кривой N4 на рис.1) при полностью открытом дросселе похожа на гору с округлой макушкой, тогда как характеристика мощности сопротивлений Nсопр. поднимается как крутая парабола. Чтобы полностью использовать арсенал мощности двигателя – и получить максимум скорости V4 (на горизонтальной трассе, без ветра), передаточное число трансмиссии и размер шин подбирают так, чтобы кривая Nсопр пересекла кривую N4 возле вершины. Максимальные скорости на третьей и пятой передачах (V3 и V5) существенно ниже. Но на спуске или с ветром вдогон выгодней может стать пятая передача, а на подъеме или с ветром в лоб – третья.
Другие враги скорости – подъем дороги и встречный ветер. Подъем с углом всего 1,5% добавит к потерям в шинах еще столько же. Но еще коварней ветер. Его скорость сложится со скоростью машины относительно дороги, – и уже эту сумму в расчете затрат мощности надо возвести в куб! При скорости по спидометру 36 км/ч (10 м/сек) и ровном встречном ветре 5 м/сек мощность Nсопр вырастет лишь на 0,9 кВт, а вот при 180 км/ч (50 м/сек) – аж на 15,5 кВт
Так зависит крутящий момент (М1…М5) или тяговая сила (Fтяг 1 …Fтяг 5) на ведущей оси от включенной передачи. При коэффициенте сцепления шин с дорогой 0,7 ведущая ось, нагруженная половиной веса машины (Gавтом = 15000 н), может создать реальную тяговую силу не больше Fмакс. доп. = 5250 Н.
На рис.2 величины крутящего момента М1…М5, а заодно и теоретические тяговые силы F1…F5 на ведущей оси, показаны одними и теми же кривыми, – ведь тяговые силы пропорциональны моментам. Величины сил – на вертикальной оси справа. Но тут важно учесть следующее.
Разгоняет машину не вся тяговая сила, а лишь избыточная – то есть разница между полной тяговой силой колес и сопротивлением воздуха. Отношение этой силы к весу машины академик Чудаков назвал динамическим фактором D. На первой передаче сопротивление воздуха мало, его можно не учитывать – считать, что машину разгоняет полная сила Fтяг.1. Но отталкиваться от дороги сильней, чем позволяет сцепление шин, невозможно! Если, например, ведущая ось несет половину веса машины – 7500 Н, то при коэффициенте сцепления φ = 0,7 тяговая сила не может превысить 35% ее веса. Это неплохо согласуется с такой официальной характеристикой любого автомобиля как предельно возможный угол подъема. С «моноприводом» трудно получить больше. Правда, у машины с задним приводом на подъемах ведущие колеса несколько догружаются весом машины, а вот передний тут невыгоден. Лучшая схема, но сложная и дорогая, – полный привод (конечно, не с такой скромной мощностью, как у «Нивы» или УАЗа!).
Если избыточная сила (на первой передаче, например) слишком велика, машина «шлифует» дорогу. Дело нелепое, нужно перейти на следующую передачу. А вот при разработке нового авто конструктор учитывает высокую мощность двигателя и ее следствие – тяговые силы в передаточных числах трансмиссии. Передачи проектируются как достаточно «длинные», расширяющие диапазон скоростей при достаточных ускорениях. А это значит, что и при более высоких скоростях действуют нужные тяговые силы (или моменты) на колесах. Иначе говоря, реализуется весь арсенал мощности! Значит, она все же важнее.
Споры на тему влияния мощности-момента ведутся давно, и конца им не видно. Вроде бы сто раз уже объясняли самыми разными способами, что тут к чему, а воз и ныне там. Вызывает неподдельный интерес, откуда все же берется заблуждение и почему оно такое устойчивое?
Причин видится две. Одна из них в том, что мощность есть функция от момента. Зависимость мощности от момента стоит барьером, который преодолеть оказывается непросто. Что странно. Поскольку очевидность того, что мощность есть функция не только от момента, но и от оборотов, не оспаривается, и тот факт, что у разных двигателей бывает весьма большой разброс по соотношению мощности к моменту, также не подвергается сомнению. То есть существует молчаливое согласие с тем, что мощность есть функция от двух аргументов — оборотов и момента, но при этом зависимость от оборотов как бы игнорируется. Почему?
А в этом и есть вторая, главная причина заблуждения. И ключевая фраза здесь: «Человек совершенно может не иметь понятие про мощность.А вот разницу в ускорении на 3 и 4 передаче он вполне способен почувствовать.» Ясно, что на динамику автомобиля оказывают большое влияние и передаточные числа КПП. На графике 1 видны кривые мощности двигателя, смещенные в зависимости от разных передаточных чисел и кривая сопротивлений. Видно, что с ростом передаточного числа динамика резко возрастает. Это очевидно и вопросов не вызывает. Странно, что не менее очевидный факт, что бОльшая часть времени при разгоне приходится вовсе не на 1 и 2 передачи, а на 3-4, при этом упускается из виду.
При разгоне здравомыслящий водитель пользуется всеми четырьмя передачами и весьма широким диапазоном частот вращения двигателя. При этом редко задумывается о том, что динамика разгона на высокой скорости мала и плохо ощущается, но именно на нее и приходится львиная доля времени разгона (по той простой причине, повторю, что на высших передачах динамика хуже и потому занимает больше времени). Хорошо ощущается динамика разгона на низших передачах, в диапазоне низких и средних оборотов (дальше водитель двигатель раскручивает редко). И что выходит? А выходит, что «низовой», моментный двигатель дает ощущение уверенного и бодрого разгона по той простой причине, что легко и весело страгивает и начинает разгонять автомобиль. А по достижении скорости ощущения становятся слабыми, и оценить разницу в разгоне 100- и 120 сильного моторов на 4-5 передачах, способен не каждый. Потому и кажется, что момент определяет динамику. По ощущениям. А ощущениям человек склонен верить очень сильно, даже вопреки логике и здравому смыслу.
Проповедующие формулировку «скорость определяется мощностью, а динамика разгона — моментом двигателя» могут убедиться в своем заблуждении, решив простую задачу.
Вводные
1. Равномерный подъем на некоторую высоту равносилен равномерному ускорению, поскольку увеличивает потенциальную энергию тела mgh*. (что можно объяснить — чем с большей высоты упадет, тем сильней ударится).
2. Поднимаем равномерно груз весом 75 кг на высоту 1 м за 1 с.
3. Имеется черный ящик, в котором спрятан мотор неизвестной природы и, возможно, редуктор с КПД=1.
Вопросы.
1. Какая мощность должна быть в моторе, спрятанном внутри черного ящика?
2. Какой момент должен быть в моторе, спрятанном внутри черного ящика?
Подъем указанного груз на нужную высоту за время аналогичен разгону по горизонтали той же массы с ускорением g в 0.5 степени или корень из g.
Если ускорение определяется моментом — просто назовите цифру
Если ускорение определяется мощностью — тоже просто назовите цифру
Если цифру назвать не удается, значит параметр может быть самым разным и роли не играет.
Вы можете разгонять тело с заданным ускорением (или поднимать его вверх), меняя крутящий момент по своей прихоти (и устанавливая каждый раз соответствующий редуктор). Вы можете отталкиваться от параметров редуктора, и всякий раз требуемый момент будет меняться и зависеть от передаточного отношения этого редуктора. Но всегда мощность будет оставаться одной и той же, неизменной величиной — для подъема груза 75 кг на 1 м за 1с понадобится ровно одна лошадиная сила или 0,73549875 кВт
Это практически ответ на цитату про «длинный коробас».
Касаемо тех-же астр, если воткнуть коробку F18 с 2.0 вместо F13 на какой-нибудь 1.2 или 1.4 двигатель, максималка не увеличится, а скорее даже и снизится, потому что передаточные числа подобраны оптимально для более мощного двигателя и с ними не будет достигнута оптимальная мощность на более слабом двигателе.
Повторюсь: будьте реалистами. Законы физики обмануть невозможно.
Если дочитали до конца, то молодцы. Надеюсь кому-нибудь когда нибудь пригодится этот материал. Можно кидать на него ссылку особо упёртым в своей правоте гонщикам))) Хотя таких людей ничего не переубедит.