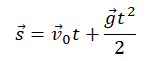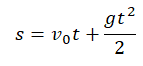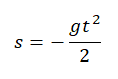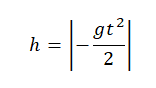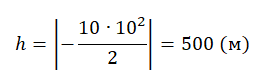Задание №1 ЕГЭ по физике
В задании №1 ЕГЭ по физике необходимо решить простую задачу по кинематике. Это может быть нахождение пути, скорости, ускорения тела или объекта по графику из условия.
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость автомобиля относительно земли ( v 1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v 2). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем данные относительно Земли:
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость второго автомобиля относительно оси ОХ ( v 2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v 1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид :
Отсюда скорость равна:
Подставляем имеющиеся данные и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Весь график можно поделить на 3 участка:
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…
Алгоритм решения
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
Скорость определяется формулой:
Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:
Скорость первого тела:
Скорость второго тела:
Отношение скорости второго тела к скорости первого тела:
pазбирался: Алиса Никитина | обсудить разбор | оценить
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Запишем исходные данные:
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем исходные данные:
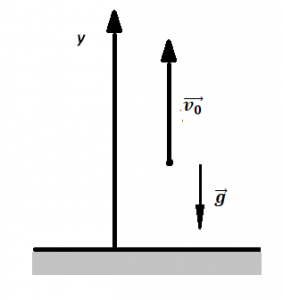
Записываем формулу для определения скорости тела в векторном виде:
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
Подставим известные данные и вычислим скорость:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем исходные данные:
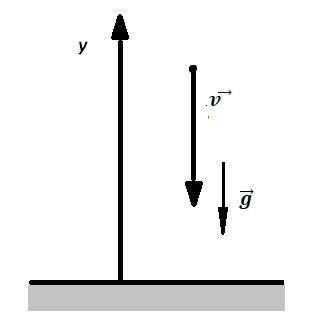
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем исходные данные:
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Контрольные тесты по физике на тему «Кинематика» 10 класс
Тест по теме «Кинематика» Вариант 1.
А) путь Б) перемещение В) смещение Г) траектория
2. В каком из следующих случаев движение тела нельзя рассматривать как движение материальной точки?
А) Движение Земли вокруг Солнца. Б) Движение спутника вокруг Земли.
В) Полет самолета из Владивостока в Москву. Г) Вращение детали, обрабатываемой на
3. Какие из перечисленных величин являются скалярными?
А) перемещение Б) путь В) скорость
4. Что измеряет спидометр автомобиля?
А) ускорение; Б) модуль мгновенной скорости;
В) среднюю скорость; Г) перемещение
5. Какая единица времени является основной в Международной системе единиц?
А) 1час Б) 1 мин В) 1 с Г) 1 сутки.
8. Какой из графиков соответствует равномерному движению? ( Рис. 1).
9. Определите путь, пройденный точкой за 5 с. (Рис. 2).
А) 2м Б) 2,5м В) 5м Г) 10м.
10.. На рисунке 3 представлен график зависимости пути, пройденного велосипедистом, от времени. Определить путь, пройденный велосипедистом за интервал времени от t 1 = 1 c до t 2 = 3с?
А) 9 м Б) 6 м В) 3 м. Г) 12 м
А) равномерное движение Б) равнозамедленное движение
В) равноускоренное движение Г) прямолинейное
12. Ускорение характеризует изменение вектора скорости
А) по величине и направлению Б) по направлению В) по величине
13. Автомобиль, движущийся прямолинейно равноускоренно, увеличил свою скорость с
3 м/с до 9 м/с за 6 секунд. С каким ускорением двигался автомобиль?
А) 0 м/с 2 Б) 3 м/с 2 В) 2 м/с 2 Г) 1 м/с 2
14. Какую скорость приобретает автомобиль при торможении с ускорением 0,5 м/с 2 через 10 с от начала торможения, если начальная скорость его была равна 72 км/ч?
А) 15м/с Б) 25м/с В) 10м/с Г) 20м/с.
Тест по теме «Кинематика» Вариант 2.
1. Велосипедист движется из точки А велотрека в точку В по кривой АВ. Назовите
физическую величину, которую изображает вектор АВ.
А) путь Б) перемещение В) скорость
2. Почему при расчетах можно считать Луну материальной точкой (относительно Земли)?
Г) Расстояние от Земли до Луны во много раз больше радиуса Луны.
5. Основными единицами длины в СИ являются:
А) метр Б) километр В) сантиметр Г) миллиметр
7. Тело, брошенное вертикально вверх, достигло наибольшей высоты 10 м и упало на
землю. Чему равны путь l и перемещение S за все время его движения?
A) l = 20 м, S = 0 м Б) l = 10 м, S = 0 B) l = 10 м, S = 20 м Г) l = 20 м, S = 10 м.
9. Определите путь, пройденный точкой за 3 с. (Рис. 2).
А) 2м Б) 6м В) 5м Г) 1,5м.
10.. На рисунке 3 представлен график зависимости пути, пройденного велосипедистом, от времени. Определить путь, пройденный велосипедистом за интервал времени от t 1 = 2 c до t 2 = 4с?
А) 9 м Б) 6 м В) 3 м. Г) 12 м
А) равномерное движение Б) равноускоренное движение
В) равнозамедленное движение Г) прямолинейное движение
12. Автомобиль трогается с места и движется с возрастающей скоростью прямолинейно.
Какое направление имеет вектор ускорения?
А) ускорение равно 0 Б) направлен против движения автомобиля
В) направлен в сторону движения автомобиля
13. Скорость автомобиля за 20с уменьшилась с 20м/с до 10м/с. С каким средним ускорением двигался автомобиль?
14. Определить скорость тела при торможении с ускорением 0,2м/с 2 через 30с от начала движения, если начальная скорость его была равна 2м/с.
Вариант 1 Вариант 2
Тело двигается вдоль оси x декартовой системы координат со скоростью 3 м/с и одновременно вдоль оси y со скоростью 4 м/с. Найти результирующую скорость.



1.13. Автомобиль трогается с места и движется с возрастающей скоростью прямолинейно.
Какое направление имеет вектор ускорения?
А) ускорение равно 0; Б) направлен против движения автомобиля;
В) направлен в сторону движения автомобиля.
1.14. Автомобиль тормозит на прямолинейном участке дороги. Какое направление имеет
вектор ускорения?
А) ускорение равно 0; Б) направлен против движения автомобиля;
В) направлен в сторону движения автомобиля.
1.16. Физические величины бывают векторными и скалярными. Какая физическая величина из перечисленных является скалярной?
А) ускорение; Б) время; В) скорость; Г) перемещение.
1.18. Основными единицами длины в СИ являются:
А) километр; Б) метр; В) сантиметр; Г) миллиметр.
1.19. Какие из перечисленных ниже величин являются векторными:
1) путь, 2) перемещение, 3) скорость?
А) 1 и 2; Б) 2; В) 2 и 3; Г) 3 и 1.
1 25. Модуль скорости тела за каждую секунду увеличивался в 2 раза. Какое утверждение будет правильным?
А) ускорение уменьшалось в 2 раза; Б) ускорение не изменялось;
В) ускорение увеличивалось в 2 раза
1.26. Тело, брошенное вертикально вверх, достигло наибольшей высоты 10 м и упало на
землю. Чему равны путь l и перемещение S за все время его движения?
A) l = 10 м, S = 0 м; Б) l = 20 м, S = 0;
B) l = 10 м, S = 20 м; Г) l = 20 м, S = 10 м.
1.35. При отходе от станции ускорение поезда составляет 1 м/с2. Какой путь проходит поезд за 10 с?
А) 5 м; Б) 10 м; В) 50 м; Г) 100 м.
1.36. При равноускоренном движении в течение 5 с автомобиль увеличил скорость от 10 до
15 м/с. Чему равен модуль ускорения автомобиля?
А) 1 м/с2; Б) 2 м/с2; В) 3 м/с2; Г) 5 м/с2.
1.65. Находящемуся на горизонтальной поверхности стола бруску сообщили скорость 5 м/с. Под действием сил трения брусок движется с ускорением 1 м/с2. Чему равен путь, пройденный бруском за 6 секунд?
А) 48 м; Б) 12 м; В) 40 м; Г) 30 м.
13. На рисунке 3 представлен график зависимости пути, пройденного велосипедистом, от времени. Определить путь, пройденный велосипедистом за интервал времени от t 1 = 1 c до t 2 = 4с?
18. Тело движется прямолинейно и уменьшает скорость. Куда направлено ускорение?
20. Почему при расчетах можно считать Луну материальной точкой (относительно Земли)?
Г) Расстояние от Земли до Луны во много раз больше радиуса Луны.
Д) Среди предложенных ответов нет правильного.
Тест №1 ЕГЭ по физике
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость автомобиля относительно земли ( v 1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v 2). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
Алгоритм решения
Решение
Записываем данные относительно Земли:
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость второго автомобиля относительно оси ОХ ( v 2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v 1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид :
Отсюда скорость равна:
Подставляем имеющиеся данные и вычисляем:
Алгоритм решения
Решение
Весь график можно поделить на 3 участка:
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…
Алгоритм решения
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
Скорость определяется формулой:
Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:
Скорость первого тела:
Скорость второго тела:
Отношение скорости второго тела к скорости первого тела:
Алгоритм решения
Решение
Запишем исходные данные:
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу для определения скорости тела в векторном виде:
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
Подставим известные данные и вычислим скорость:
Алгоритм решения
Решение
Записываем исходные данные:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Алгоритм решения
Решение
Записываем исходные данные:
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем: