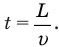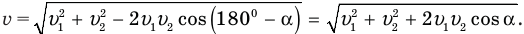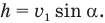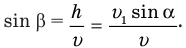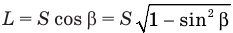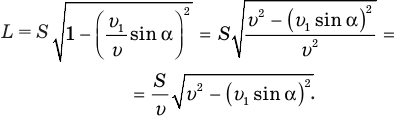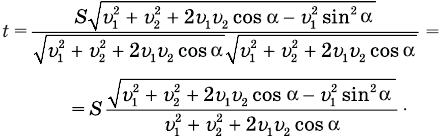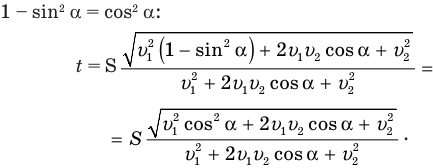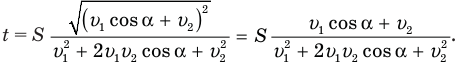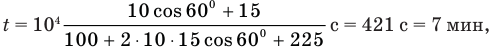Два автомобиля движутся после развилки по двум дорогам расходящимся под углом 60
Цитата: deviance написал 8 окт. 2010 20:52
Небольшому грузу массой 600г, лежащему на длинной доске массой 1 кг, толчком сообщили скорость 4 м/c, направленную вдоль доски. До этого толчка доска покоилась на гладкой горизонтальной плоскости. Найти работу сил трения между грузом и доской к моменту, когда груз перестанет скользить по доске.
Заранее спасибо!
Проще всего задача решается с использованием теоремы об изменении кинетической энергии центра масс системы. (Ответ. A=-mM/(m+M)v 2 /2). Какие у Вас идеи? Можем обсудить.
Желаю успеха, ZVlad.
(Сообщение отредактировал ZVlad 9 окт. 2010 21:50)
| mariso4335 |       что означает альфа в коэффициенте стьюдента и как ее найти что означает альфа в коэффициенте стьюдента и как ее найти |
| Всего сообщений: 2 | Присоединился: октябрь 2010 | Отправлено: 9 окт. 2010 16:31 | IP |
| deviance |       Уважаемый ZVlad, прочтите, пожалуйста, ЛС! Уважаемый ZVlad, прочтите, пожалуйста, ЛС! Заранее спасибо. |
| Всего сообщений: 4 | Присоединился: октябрь 2010 | Отправлено: 9 окт. 2010 18:30 | IP |
| ZVlad |     
Конечно, Вы можете вместо понятия скорости центра масс использовать закон сохранения импульса. |
| Всего сообщений: 137 | Присоединился: апрель 2007 | Отправлено: 9 окт. 2010 21:49 | IP |
| Mihn |      1) Два автомобиля подъезжают к развилке дороги со скоростями 72 и 54 км/ч и разъежаются по двум дорогам, угол между которыми 60градусов. Определите скорость первого автомобиля относительно второго:1) До развилки 2) после развилки. Благодарю 1) Два автомобиля подъезжают к развилке дороги со скоростями 72 и 54 км/ч и разъежаются по двум дорогам, угол между которыми 60градусов. Определите скорость первого автомобиля относительно второго:1) До развилки 2) после развилки. Благодарю Ответ: 18км/ч и 65 км/ч. Пацаны помогите по возможности, охота самому ещё понять. (Сообщение отредактировал Mihn 10 окт. 2010 10:03) |
| Всего сообщений: 9 | Присоединился: октябрь 2010 | Отправлено: 10 окт. 2010 10:02 | IP |
| ZVlad |     
(Сообщение отредактировал Mihn 10 окт. 2010 10:03) Первый ответ очевидный: автомобили движутся в одном направлении вдоль прямой. Поэтому, V2-V1= 18 (км/ч). Желаю успехов, ZVlad |
| Всего сообщений: 137 | Присоединился: апрель 2007 | Отправлено: 10 окт. 2010 10:44 | IP |
| ART 95 |       Пожалуйста, помогите решить: Пожалуйста, помогите решить: Шумахер прошел финишный отрезок гоночной трассы со скоростью 70 м/с, Виталий Петров появился на этом отрезке с задержкой на 1 с относительно Шумахера, но через 10 с после своего появления догнал его и пришел первым. С какой скоростью двигался россиянин? |
| Всего сообщений: 9 | Присоединился: октябрь 2010 | Отправлено: 10 окт. 2010 11:06 | IP |
| Larka92 |      Помогите решить Помогите решить 1. Материальная точка массой m = 1,0 кг движется вдоль оси x под действием периодической силы F = F0 cosωt (F0 = 10 Н, ω = 1,0 рад/с), 2. Стационарный спутник связи постоянно находится над одной и той же точкой экватора. Определить его высоту h над поверхностью Земли. 2. Велосипедист массы M = 50 кг скатывается по наклонной дорожке и делает «мертвую петлю» радиуса R = 3,5 м. Определить минимальную высоту h, с которой должен съехать велосипедист, чтобы не оторваться от дорожки в верхней точке петли. Масса велосипеда m = 15 кг, причем на колеса приходится масса m0 = 4,0 кг. Колеса считать обручами. По двум пересекающимся под углом 60° дорогам движутся два автомобиля с одинаковыми скоростями, равными 20 м / с?По двум пересекающимся под углом 60° дорогам движутся два автомобиля с одинаковыми скоростями, равными 20 м / с. Через какое время после встречи у перекрестка расстояние между ними станет равным 3 км? За какое время автомобиль, движущийся со скоростью 72км / ч, догонит автомобильь, движущийся со скоростью 36км / ч, если расстояние между ними равно 1000км?За какое время автомобиль, движущийся со скоростью 72км / ч, догонит автомобильь, движущийся со скоростью 36км / ч, если расстояние между ними равно 1000км? Две моторные лодки движутся вдоль берега озера навстречу друг другу?Две моторные лодки движутся вдоль берега озера навстречу друг другу. Скорость каждой лодки равна 3м / с. Через какое время после встречи расстояние между лодками станет равным 120м? Через сколько секунд после их встречи на перекрестке расстояние между ними станет равным 625 м? Две моторные лодки движутся вдоль берега озера навстречу друг другу?Две моторные лодки движутся вдоль берега озера навстречу друг другу. Скорость каждой лодки равна 3 м / с. Через какое время после встречи расстояние между лодками станет равным 120 м? Два автомобиля движутся навстречу друг другу со скоростями 12 м / с и 8 м / с, соответственно?Два автомобиля движутся навстречу друг другу со скоростями 12 м / с и 8 м / с, соответственно. Начальное расстояние между ними равно 600м. Найдите время их встречу. По двум пересекающимся под углом 60° дорогам движутся два автомобиля с одинаковыми скоростями, равными 20 м / с. Через какое время после встречи у перекрестка расстояние между ними станет равным 3 км? Автомобиль затратил на прохождение пути время t. Чему равна средняя скорость автомобиля. Два спортсмена движутся по пересекающимся под углом 60 градусов прямым дорожкам с одинаковыми по модулю скоростями?Два спортсмена движутся по пересекающимся под углом 60 градусов прямым дорожкам с одинаковыми по модулю скоростями. Через промежуток времени t = 1 мин после их встречи в месте пересечения дорожек расстояние между ними стало l = 200м. Найдите модули скоростей движения спортсменов. Автомобиль и мотоциклист движутся навстречу друг другу со скоростями, модули которых равны 30 м / с и 20 м / с соответственно?Автомобиль и мотоциклист движутся навстречу друг другу со скоростями, модули которых равны 30 м / с и 20 м / с соответственно. Расстояние между ними в начальный момент времени равно 150 м. Найдите аналитическим способом время встречи автомобиля с мотоциклистом и расстояние, которое проехал мотоциклист. Пожалуйста помогите решить. Два спортсмена движутся по пересекающимся под углом α = 60° прямым дорожкам с одинаковыми по модулю скоростями?Два спортсмена движутся по пересекающимся под углом α = 60° прямым дорожкам с одинаковыми по модулю скоростями. Через промежуток времени 10 мин. После их встрече в месте пересечения дорожек расстояние между ними стало l = 200 м. Найдите модули скоростей движения спортсменов. Научный форум dxdyМатематика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия, |
Задачки по кинематике
Здравствуйте! Ниже ряд задач с которыми у меня проблемы. Прошу помочь разобраться.
Задача №1
Лодка перевозит людей с одного берега реки на другой. Нужно найти куда лодке плыть, чтобы она затратила наименьшее время. В ответе сказано, что минимальным время будет, если скорость лодки направлена под прямым углом к берегу. Но почему это будет минимальное время?
Задача №2
В решении предлагают перейти в одну из галактик и определить скорость второй галактике относительно первой.
Вопрос 1. Разве можно искать скорость второй галактики относительно первой? Ведь первая галактика не ИСО. Значит преобразования Галилея верны и для неИСО?
Вопрос 2. Если в открытом космосе в какой то произвольной точке пространства измерить (относительно себя) скорость двух этих галактик. Так как мы неподвижны относительно центра Большого Взрыва, то обе измеренные скорости будут абсолютными. Значит мы найдём 


До развилки решил. А вот после развилки получаю ответ 109.5 км/ч. А в ответах 65 км/ч. Кто прав я или авторы?
Задача №4
Вообще не знаю как подступиться к решению. Наведите, пожалуйста, на верный путь.
Задача №5
Ищу среднее ускорение по формуле 

| Заслуженный участник |
2.1 В какое-то мгновение выберем систему отсчета такую, что бы скорость галлактики (выбранной) была 0 (в следующую секунду это может быть уже не так). В этот момент времени все быстренько сосчитаем, пока не началось.
3. Непонятно, как подъезжают, и как разъезжаются.
| Заслуженный участник |
Последний раз редактировалось arseniiv 02.01.2015, 21:43, всего редактировалось 1 раз.
Потому что время зависит только от слагаемого скорости, перпендикулярного берегам, а течение как раз в него не вкладывается. Значит, нам придётся.
С задачей №4 смотрите лучше на зонт. Если капля упала на зонт, она не опасна, так что надо удостовериться, что человек проецируется на зонт целиком. Направление проекции задаёт как раз скорость капель. Видимо, предполагается, что сам человек, в отличие от зонта, перпендикулярен поверхности. Тогда при некоторых направлениях движения капель он проецироваться на зонт, как его ни поворачивай, не сможет. Вам надо только угадать, почему капли должны падать на зонт нормально.
Как так нулю? Скорость сменила направление, т. е. изменилась.
Задача C8. Два автомобиля движутся co скоростями 36 км/ч и 54 км/ч под углом = 60° друг к другу. В некоторый момент времени один из них оказался в пункте М, а другой в тот же момент — в пункте N, расстояние между которыми S = 10 км.
Задача C8. Два автомобиля движутся co скоростями 36 км/ч и 54 км/ч под углом 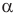
Через какой промежуток времени t расстояние между автомобилями станет минимальным?
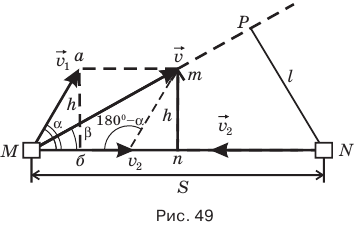
Обозначим v — скорость автомобиля слева на рис. 49, 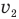
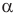
t — промежуток времени, через который расстояние между автомобилями станет минимальным, v — скорость автомобиля слева, если бы автомобиль справа был неподвижен, l — кратчайшее расстояние между обоими автомобилями, L — путь, пройденный левым автомобилем со скоростью V, Р — один из острых углов треугольника Мmn, h — длину перпендикуляра, опущенного из конца вектора 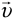
Решение:
Как же определить момент времени, когда расстояние между автомобилями станет наименьшим? Они же все время едут, причем каждый со своей скоростью — попробуй поймать этот самый момент.
Сразу дадим совет: при решении подобных задач, когда два тела одновременно движутся относительно друг друга, примите одно из них, например, автомобиль справа, за неподвижное, тогда можно считать, что автомобиль слева, продолжая двигаться со своей скоростью 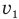
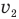
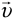
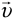
Если теперь из точки N, где находится правый неподвижный автомобиль, опустить перпендикуляр NP на эту траекторию, то длина этого перпендикуляра l и будет тем самым кратчайшим расстоянием между обоими автомобилями. Искомый промежуток времени t можно найти, если разделить путь L, пройденный левым автомобилем со скоростью v и равный длине отрезка МР, на эту скорость:
Скорость v найти несложно. В тупоугольном треугольнике скоростей вектор этой скорости лежит против тупого угла, равного 180° — 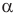
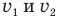
Труднее определить длину отрезка L = МР. Этот отрезок является катетом в прямоугольном треугольнике MPN, где гипотенузой служит известное нам расстояние S=MN, а другим катетом — неизвестный отрезок l. Этот треугольник прямоугольный, но и от этого мало радости, ведь отрезок l взять неоткуда. Вот если бы в этом треугольнике нам был известен очень острый угол PMN, мы тогда могли найти катет L через прилежащий к этому катету угол PMN и гипотенузу S.
Но как определить этот острый угол? Обозначим его как-нибудь, например, 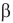
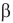
Вот если бы как-нибудь найти этот h. Может, опустить из конца вектора скорости 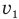
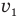
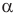
Зная h, находим из прямоугольного треугольника Мmn 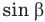
Теперь уже просто. Из прямоугольного треугольника MPN выражаем катет L через известную нам гипотенузу S и найденный угол 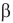
Нам осталось подставить правые части равенств (2) и (5) в формулу (1), и непростая задача, потребовавшая от нас столько выдумки и сообразительности, будет решена. Подставляем:
В общем-то задача решена, но хорошо бы полученную формулу упростить. Сделать это несложно. Достаточно сгруппировать под корнем первый и последний члены, вынести 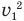
Теперь мы видим, что под корнем стоит квадрат суммы величин 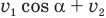
Выразим все величины в единицах СИ: 36 км/ч = 10 м/с, 54 км/ч = 15 м/с, 10 км = 1- 10* м.
Подставим числа и произведем вычисления:
Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти задачи:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института