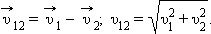Два автомобиля равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекре…
В начальный момент времени расстояние между машинами по теореме Пифагора
S0 = √(16^2 + 12^2) = √(256 + 144) = √400 = 20 км.
Расстояние от 1 машины до перекрестка меняется по закону:
s1 = 16 — 65*t км, где t — время в часах.
Расстояние от 2 машины до перекрестка меняется по закону:
Расстояние между машинами по той же теореме Пифагора
Вычислим минимум этой функции, который будет в вершине параболы
В этот момент машины проехали
s2 = 12 — 45*t0 = (12*625 — 45*158)/625 = 390/625 = 78/125
16÷65=16/65 ч первый а/м достигнет перекрестка.
(16/65)*45=11 1/13 км проедет второй а/м, когда первый достигнет перекрёстка.
12-11 1/3=12/13 км будет расстояние между первым а/м и вторым а/м.
Дальше смотрите рисунок к задаче, на рисунке перекрёсток. По началу я думал, что самая короткая гипотенуза между автомобилями будет тогда, когда расстояния от перекрёстка до первого и второго автомобиля будут равны. Оно бы так и было, если бы скорости у первого и второго автомобиля были бы равные.
В данном случае расстояние между автомобилями будет меняться по гипотенузе прямоугольного треугольника, когда первый автомобиль удаляется от перекрестка, а второй приближаться к перекрёстку (находясь от него на расстоянии 12/13 км.) Если записать функцию как квадрат гипотенузы, то:
Найдем наименьшее значение функции:
(1080/13)/(2*6250)=54/8125 часа после движения первого автомобиля от перекрёстка расстояние между автомобилями будет наименьшим.
16/65+54/8125=0,2528 часа=15,168 минут после начала движения, расстояние между автомобилями будет наименьшим.
(54/8125)*65=54/125 км проехал первый автомобиль от перекрёстка за 54/8125 часа.
(12/13)-(54/8125)*45=(12/13)-(486/1625)=78/125 км расстояние до перекрестка второго автомобиля, когда первый автомобиль отъехал от перекрестка на 54/125 км.
Найдём наименьшее расстояние между автомобилями по теореме Пифагора.
S=√(54/125)²+(78/125)²≈0,758946638≈0,76 км. наименьшее расстояние между автомобилями.
Ответ: через 15,168 минут после начала движения, расстояние между автомобилями будет наименьшим: ≈ 0,76 км.
Два автомобиля движутся по взаимно перпендикулярным дорогам по направлению к перекрестку в некоторый
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние? Считайте, что перекресток не T-образный, обе дороги продолжаются за перекрестком.
Обозначим буквой t время, прошедшее с начального момента времени. Поскольку каждый велосипедист движется по взаимно перпендикулярным дорогам, то расстояние между ними может быть вычислено по теореме Пифагора. Рассмотрим f (t) — квадрат длины в каждый момент времени, тогда:
Итак, У данной квадратичной функции есть наименьшее значение, которое достигается при
мин. Найдем его:
Таким образом минимальное расстояние между велосипедистами равно км, и будет достигнуто через
мин.
Ответ: мин,
км.
Условие уточнено редакцией Решу ЕГЭ.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
В условии сказано, что велосипедисты движутся по направлению к перекрестку и ничего не сказано, куда они будут двигаться, достигнув этого перекрёстка, и будут ли вообще куда-то двигаться. И даже продолжается ли каждая из дорог после этого перекрёстка нам тоже неизвестно (бывают ведь и Т-образные перекрёстки). И остаются ли они на этом продолжении, если таковое имеется, по-прежнему взаимно перпендикулярными.
На мой взгляд, правильным решением будет тот момент, когда второй велосипедист достигнет перекрёстка, то есть через шесть минут. Ведь именно в этот момент они оба ещё двигались по направлению к перекрестку. К этому моменту первый велосипедист будет на расстоянии 1 км от перекрёстка и от второго велосипедиста. То есть при решении задачи минимум функции f(t) следует искать на отрезке от 0 до 0,1 часа. В предложенном же на сайте варианте решения второй велосипедист уже почти целую минуту движется по направлению от перекрестка, что не соответствует условию задачи.
 Задачи с решениями
Задачи с решениями 

Решение
Первый способ.
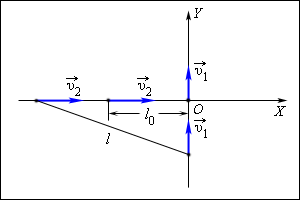
Положение каждого из автомобилей в любой момент времени можно задать двумя координатами. Выберем Землю в качестве тела отсчета. Направим координаты оси и вдоль дорог в направлении движения автомобилей (рис. 1.2.1). За начало координат выберем перекресток, за начало отсчета времени – момент пересечения перекрестка первым автомобилем. Уравнения движения автомобилей записываются в виде:
Расстояние между автомобилями в любой момент времени равно
 | ||
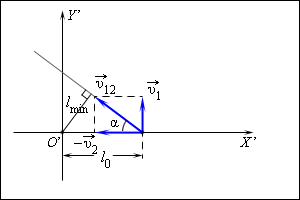
| Рисунок 1.2.1. В качестве тела отсчета выберем второй автомобиль; направление координатных осей и и начало отсчета времени примем такими же, как и в первом способе решения задачи. В системе отсчета, связанной со вторым автомобилем, первый автомобиль движется со скоростью Эта скорость направлена под некоторым углом к прямой, соединяющей автомобили в начальный момент времени (рис. 1.2.2).
|

 Задачи с решениями
Задачи с решениями 

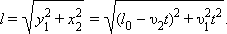
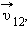 равной:
равной: