Относительное движение
Скорость точки относительно неподвижной системы отсчета равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы.
\(v\) — абсолютная скорость
\(\vec\) — переносная скорость
\(v’\) — относительная скорость
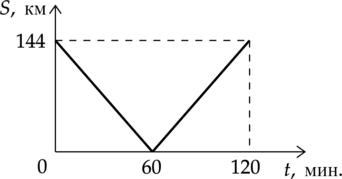
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?
За 60 минут расстояние между автомобилями изменилось с 144 км до 0 км, то есть автомобили встретились. Вычислим скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем: \[v=\dfrac<144000\text< м>><3600\text< с>>=40\text< м/с>\]
Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Так как пассажир идет в том же направлении, что и автобус, то вектора их скоростей складываются, поэтому абсолютная скорость равна \[\upsilon_<\text<абс>>=\upsilon_<\text<пер>>+\upsilon_<\text<отн>>=10\text< м/с>+1\text< м/с>=11\text< м/с>\]
По прямой дороге с постоянной скоростью 100 км/ч едет мотоциклист и в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 8 км/ч. Река течёт со скоростью 6 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.
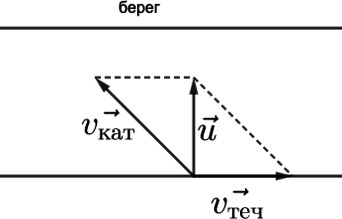
Чтобы катер двигался перпендикулярно относительно берега, относительно воды ему надо двигаться под углом. По закону сложения скоростей: \[\vec
По теореме Пифагора найдем скорость катера относительно воды: \[v_<\text<кат>>=\sqrt
Пассажир зашел в автобус через заднюю дверь. Автобус поехал с постоянной скоростью \(\upsilon_1=25\) м/с, а пассажир пошел к передней части автобуса. Скорость пассажира относительно автобуса равна \(\upsilon_<2>=3\) м/с. С какой скоростью едет автобус относительно пассажира?
Скорость первого тела относительного второго равна скорости второго тела относительно первого и направлена в противоположную сторону. \[\vec