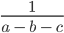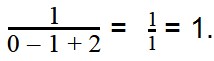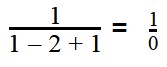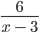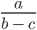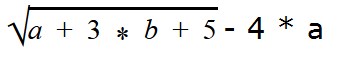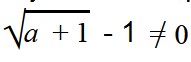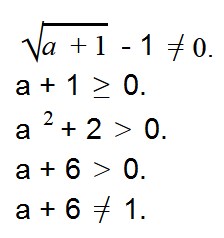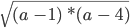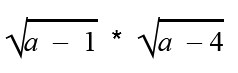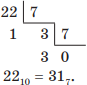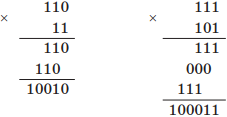Приведите по одному примеру допустимых и недопустимых значений для каждой из величин : А) температура человека ; Б) скорость автор ; В) площадь государства ; Г) название дня недели?
Приведите по одному примеру допустимых и недопустимых значений для каждой из величин : А) температура человека ; Б) скорость автор ; В) площадь государства ; Г) название дня недели.
Могут ли разные объекты описываться одной и той же моделью?
Могут ли разные объекты описываться одной и той же моделью?
Является ли природа источником информации для человека?
Является ли природа источником информации для человека?
Приведи пример из своей жизни.
(C + + ) В структурах U[7], D[7], V[7] содержатся значения утренней, дневной и вечерней температуры соответственно за каждый день недели?
(C + + ) В структурах U[7], D[7], V[7] содержатся значения утренней, дневной и вечерней температуры соответственно за каждый день недели.
Подсчитать среднее значение дневной температуры за каждый день.
Температура воздуха за неделю принимала следующие значения : 17, 15, 14, 24, 27, 30, 28?
Температура воздуха за неделю принимала следующие значения : 17, 15, 14, 24, 27, 30, 28.
В какой день еедели температура была максимальной.
Приведите примеры изменения значений свойств объекта в результате действия самого объекта?
Приведите примеры изменения значений свойств объекта в результате действия самого объекта.
Использования слов в прямом и переносном значение приведите примеры?
Использования слов в прямом и переносном значение приведите примеры?
Напишите программу, которая вычисляет среднюю за неделю температуру воздуха?
Напишите программу, которая вычисляет среднюю за неделю температуру воздуха.
Исходные данные вводятся с клавиатуры.
Пример выходных данных : Введите температуру Понедельник> ; > ; 12 Вторник> ; > ; 10 Среда> ; > ; 16 Четверг> ; > ; 18 Пятница> ; > ; 17 Суббота> ; > ; 16 Воскресенье> ; > ; 14 Пример выходных данных : Средняя температура за неделю : 14.
Написать программу выбора дня недели, не используя оператора выбора case a of?
Написать программу выбора дня недели, не используя оператора выбора case a of.
Каждый день пронумерован от 1 до 7.
Напишите программу которая вычисляет среднюю за неделю температуру воздуха?
Напишите программу которая вычисляет среднюю за неделю температуру воздуха.
Исходные данные вводятся с клавиатуры Средняя температура за неделю 14.
Область допустимых значений функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 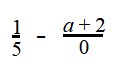
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Пример 7
Найдем ОДЗ переменной a в выражении
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 8
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Скорость. Единицы скорости
Содержание
Механическое движение имеет множество характеристик. Вы уже узнали, что оно относительно и бывает разных видов: прямолинейное и криволинейное, равномерное и неравномерное.
Тела движутся по воображаемым линиям, которые называются траекториями, а длина траектории – это путь, который проходит тело.
В этом уроке мы рассмотрим новую физическую величину, характеризующую движение – скорость.
Скорость при равномерном движении
Взгляните на рисунок 1. Если мы предположим, что бегуны, велосипедисты и автомобили двигаются равномерно, то чем будет отличаться их движение?

В таких случаях обычно мы говорим, что машина будет двигаться быстрее, чем велосипедист, а велосипедист – быстрее, чем бегун. Здесь, в физике, появляется такая величина, как скорость.
Скорость – это физическая величина, характеризующая быстроту движения тел
В нашем случае люди пробегают 15 км за 1 час, велосипедисты проезжают 25 км за 1 час, а машина за то же время – 60 км, т.е. движутся с различными скоростями.
Скорость при равномерном движении тела показывает, какой путь проходит тело в единицу времени
Скорость при равномерном движении постоянна
Как вычислить скорость
Чтобы определить скорость при равномерном движении, нужно путь, пройденный телом за выбранный промежуток времени, разделить на этот промежуток времени:
$$\upsilon = \large \frac
Cкорость тела при равномерном движении – это величина, равная отношению пути ко времени, за которое пройден этот путь.
Скорость при неравномерном движении
При неравномерном движении тело проходит разные пути за равные промежутки времени, т.е. скорость тела изменяется от одного участка пути к другому.
Как же определить скорость на всем пути? Здесь нам поможет понятие средней скорости.
Чтобы определить среднюю скорость тела при неравномерном движении, надо весь пройденный путь разделить на все время движения:
Отметим, что средняя скорость описывает движение тела за весь промежуток времени. В это время тело можно замедляться, разгоняться, останавливаться.
Например, если вы выезжаете на автомобиле из Москвы в Санкт-Петербург (рисунок 2), то весь путь займет у вас 10 ч. В это время машина будет то набирать скорость, то тормозить, сделает остановку. Общий путь, который вы при этом проедите, будет равен 600 км.
Средняя скорость движения автомобиля будет равна:
$\upsilon_ <ср>= \frac

Взгляните на таблицу 1, где приведены различные средние скорости.
Единицы измерения скорости
За за единицу скорости принимают скорость такого равномерного движения, при котором за 1 секунду тело проходит путь длиной 1 метр.
Следственно, скорость в системе СИ – количество метров, которое тело пройдёт за 1 секунду.
В повседневной жизни мы чаще видим, что скорость измеряют в километрах в час $\frac<км><ч>$. Также можно использовать километры в секунду $\frac<км><с>$ и сантиметры в секунду $\frac<см><с>$.
Так мы увидели, что числовое значение скорости зависит от выбранной единицы измерения.
Скорость как вектор
Логично, что, кроме числового значения, скорость имеет и направление. Например, чтобы узнать, где будет находиться велосипедист через 1 час после того, как он выехал из дома, нам необходимо знать скорость движения и ее направление.
Физические величины делятся на те, которые имеют направление и те, которые его не имеют – на векторные и скалярные:
1. Векторные величины – это величины, которые, кроме числового значения (модуля), имеют еще и направление.
Скорость – это векторная физическая величина
На рисунке 3 стрелкой показано направление скорости (направление движение тела).

2. Скалярные величины – это физические величины, которые не имеют направления и характеризуются только числовым значением. Это путь, объем, время, длина, масса и др.
Примеры задач на нахождение скорости
1. Равномерно двигаясь, поезд за 3 часа прошел путь длиной 152 км. Найдите скорость движения поезда в единицах СИ.
Дано:
$S = 152 км$
$t = 3 ч$
Показать решение и ответ
Решение:
$\upsilon = \frac
$\upsilon = \frac<152> <3>\frac<км> <ч>\approx 51 \frac<км> <ч>$.
Выразим в единицах СИ:
$51 \frac<км> <ч>= \frac<51 000> <3600>\frac<м>
Рисунок 4. Схема движения лыжника.
Дано:
$\upsilon_1 = 20 \frac<км><ч>$
$t_1 = 15$ мин
$\upsilon_2 = 10 \frac<км><ч>$
$t_2 = 45$ мин
Найти:
$\upsilon_ <ср>-?$
Показать решение и ответ
Чтобы найти среднюю скорость лыжника, нужно его полный путь разделить на все время движения:
$\upsilon_ <ср>= \frac
Скорость передачи информации, объем памяти
Теория к заданию 9 из ЕГЭ по информатике
Информация и ее кодирование
Различные подходы к определению понятия «информация». Виды информационных процессов. Информационный аспект в деятельности человека
Информация (лат. informatio — разъяснение, изложение, набор сведений) — базовое понятие в информатике, которому нельзя дать строгого определения, а можно только пояснить:
Понятие «информация» является общенаучным, т. е. используется в различных науках: физике, биологии, кибернетике, информатике и др. При этом в каждой науке данное понятие связано с различными системами понятий. Так, в физике информация рассматривается как антиэнтропия (мера упорядоченности и сложности системы). В биологии понятие «информация» связывается с целесообразным поведением живых организмов, а также с исследованиями механизмов наследственности. В кибернетике понятие «информация» связано с процессами управления в сложных системах.
Основными социально значимыми свойствами информации являются:
В человеческом обществе непрерывно протекают информационные процессы: люди воспринимают информацию из окружающего мира с помощью органов чувств, осмысливают ее и принимают определенные решения, которые, воплощаясь в реальные действия, воздействуют на окружающий мир.
Информационный процесс — это процесс сбора (приема), передачи (обмена), хранения, обработки (преобразования) информации.
Сбор информации — это процесс поиска и отбора необходимых сообщений из разных источников (работа со специальной литературой, справочниками; проведение экспериментов; наблюдения; опрос, анкетирование; поиск в информационно-справочных сетях и системах и т. д.).
Передача информации — это процесс перемещения сообщений от источника к приемнику по каналу передачи. Информация передается в форме сигналов — звуковых, световых, ультразвуковых, электрических, текстовых, графических и др. Каналами передачи могут быть воздушное пространство, электрические и оптоволоконные кабели, отдельные люди, нервные клетки человека и т. д.
Хранение информации — это процесс фиксирования сообщений на материальном носителе. Сейчас для хранения информации используются бумага, деревянные, тканевые, металлические и другие поверхности, кино- и фотопленки, магнитные ленты, магнитные и лазерные диски, флэш-карты и др.
Обработка информации — это процесс получения новых сообщений из имеющихся. Обработка информации является одним из основных способов увеличения ее количества. В результате обработки из сообщения одного вида можно получить сообщения других видов.
Защита информации — это процесс создания условий, которые не допускают случайной потери, повреждения, изменения информации или несанкционированного доступа к ней. Способами защиты информации являются создание ее резервных копий, хранение в защищенном помещении, предоставление пользователям соответствующих прав доступа к информации, шифрование сообщений и др.
Язык как способ представления и передачи информации
Для того чтобы сохранить информацию и передать ее, с давних времен использовались знаки.
В зависимости от способа восприятия знаки делятся на:
Для долговременного хранения знаки записывают на носители информации.
Для передачи информации используются знаки в виде сигналов (световые сигналы светофора, звуковой сигнал школьного звонка и т. д.).
По способу связи между формой и значением знаки делятся на:
Для представления информации используются знаковые системы, которые называются языками. Основу любого языка составляет алфавит — набор символов, из которых формируется сообщение, и набор правил выполнения операций над символами.
Системы счисления также можно рассматривать как формальные языки. Так, десятичная система счисления — это язык, алфавит которого состоит из десяти цифр 0..9, двоичная система счисления — язык, алфавит которого состоит из двух цифр — 0 и 1.
Методы измерения количества информации: вероятностный и алфавитный
Единицей измерения количества информации является бит. 1 бит — это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.
Связь между количеством возможных событий N и количеством информации I определяется формулой Хартли:
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка (алфавит) можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ:
Например, в русском языке 32 буквы (буква ё обычно не используется), т. е. количество событий будет равно 32. Тогда информационный объем одного символа будет равен:
I = log2 32 = 5 битов.
Если N не является целой степенью 2, то число log2N не является целым числом, и для I надо выполнять округление в большую сторону. При решении задач в таком случае I можно найти как log2N’, где N′ — ближайшая к N степень двойки — такая, что N′ > N.
Например, в английском языке 26 букв. Информационный объем одного символа можно найти так:
N = 26; N’ = 32; I = log2N’ = log2(2 5 ) = 5 битов.
Если количество символов алфавита равно N, а количество символов в записи сообщения равно М, то информационный объем данного сообщения вычисляется по формуле:
Примеры решения задач
Пример 1. Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
Пример 2. Метеорологическая станция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
Решение. В данном случае алфавитом является множество целых чисел от 0 до 100. Всего таких значений 101. Поэтому информационный объем результатов одного измерения I = log2101. Это значение не будет целочисленным. Заменим число 101 ближайшей к нему степенью двойки, большей 101. Это число 128 = 27. Принимаем для одного измерения I = log2128 = 7 битов. Для 80 измерений общий информационный объем равен:
80 · 7 = 560 битов = 70 байтов.
Вероятностный подход к измерению количества информации применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
$N$ — количество возможных событий;
Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Единицы измерения количества информации
Наименьшей единицей информации является бит (англ. binary digit (bit) — двоичная единица информации).
Бит — это количество информации, необходимое для однозначного определения одного из двух равновероятных событий. Например, один бит информации получает человек, когда он узнает, опаздывает с прибытием нужный ему поезд или нет, был ночью мороз или нет, присутствует на лекции студент Иванов или нет и т. д.
В информатике принято рассматривать последовательности длиной 8 битов. Такая последовательность называется байтом.
Производные единицы измерения количества информации:
1 килобайт (Кб) = 1024 байта = 2 10 байтов
1 мегабайт (Мб) = 1024 килобайта = 2 20 байтов
1 гигабайт (Гб) = 1024 мегабайта = 2 30 байтов
1 терабайт (Тб) = 1024 гигабайта = 2 40 байтов
Процесс передачи информации. Виды и свойства источников и приемников информации. Сигнал, кодирование и декодирование, причины искажения информации при передаче
Информация передается в виде сообщений от некоторого источника информации к ее приемнику посредством канала связи между ними.
В качестве источника информации может выступать живое существо или техническое устройство. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал.
Сигнал — это материально-энергетическая форма представления информации. Другими словами, сигнал — это переносчик информации, один или несколько параметров которого, изменяясь, отображают сообщение. Сигналы могут быть аналоговыми (непрерывными) или дискретными (импульсными).
Сигнал посылается по каналу связи. В результате в приемнике появляется принимаемый сигнал, который декодируется и становится принимаемым сообщением.
Передача информации по каналам связи часто сопровождается воздействием помех, вызывающих искажение и потерю информации.
Примеры решения задач
Пример 1. Для кодирования букв А, З, Р, О используются двухразрядные двоичные числа 00, 01, 10, 11 соответственно. Этим способом закодировали слово РОЗА и результат записали шестнадцатеричным кодом. Указать полученное число.
Решение. Запишем последовательность кодов для каждого символа слова РОЗА: 10 11 01 00. Если рассматривать полученную последовательность как двоичное число, то в шестнадцатеричном коде оно будет равно: 1011 01002 = В416.
Скорость передачи информации и пропускная способность канала связи
Прием/передача информации может происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации, или скорость информационного потока.
Скорость выражается в битах в секунду (бит/с) и кратных им Кбит/с и Мбит/с, а также в байтах в секунду (байт/с) и кратных им Кбайт/с и Мбайт/с.
Максимальная скорость передачи информации по каналу связи называется пропускной способностью канала.
Примеры решения задач
Пример 1. Скорость передачи данных через ADSL-соединение равна 256000 бит/с. Передача файла через данное соединение заняла 3 мин. Определите размер файла в килобайтах.
Решение. Размер файла можно вычислить, если умножить скорость передачи информации на время передачи. Выразим время в секундах: 3 мин = 3 ⋅ 60 = 180 с. Выразим скорость в килобайтах в секунду: 256000 бит/с = 256000 : 8 : 1024 Кбайт/с. При вычислении размера файла для упрощения расчетов выделим степени двойки:
Размер файла = (256000 : 8 : 1024) ⋅ (3 ⋅ 60) = (2 8 ⋅ 10 3 : 2 3 : 2 10 ) ⋅ (3 ⋅ 15 ⋅ 2 2 ) = (2 8 ⋅ 125 ⋅ 2 3 : 2 3 : 2 10 ) ⋅ (3 ⋅ 15 ⋅ 2 2 ) = 125 ⋅ 45 = 5625 Кбайт.
Представление числовой информации. Сложение и умножение в разных системах счисления
Представление числовой информации с помощью систем счисления
Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.
Система счисления — это система записи чисел с помощью определенного набора цифр.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.
Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.
Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.
Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.
Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.
Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.
Развернутая форма записи чисел произвольной системы счисления имеет вид
$a$ — цифры численной записи, соответствующие разрядам;
$m$ — количество разрядов числа дробной части;
$n$ — количество разрядов числа целой части;
$q$ — основание системы счисления.
Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.
Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В12 можно расписать так:
В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.
Перевод чисел в позиционных системах счисления
Перевод чисел из произвольной системы счисления в десятичную
Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:
11012 = 1 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 1310;
17D,ECH = 12 ⋅ 16 –2 + 14 ⋅ 16 –1 + 13 ⋅ 160 + 7 ⋅ 16 1 + 1 ⋅ 16 2 = 381,921875.
Перевод чисел из десятичной системы счисления в заданную
Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
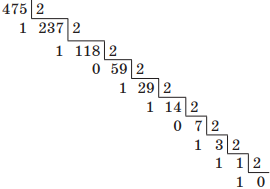
Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:
Читая остатки от деления снизу вверх, получим 111011011.
1 ⋅ 2 8 + 1 ⋅ 2 7 + 1 ⋅ 2 6 + 0 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 47510.
Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.
Например, переведем десятичную дробь 0,37510 в двоичную систему счисления:
Полученный результат — 0,0112.
Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2 І ; І = 3).
Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.
1234,7778 = 001 010 011 100,111 111 1112 = 1 010 011 100,111 111 1112;
12345678 = 001 010 011 100 101 110 1112 = 1 010 011 100 101 110 1112.
При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.
Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2 І ; І = 4).
Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.
Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.
1234,AB7716 = 0001 0010 0011 0100,1010 1011 0111 01112 = 1 0010 0011 0100,1010 1011 0111 01112;
CE456716 = 1100 1110 0100 0101 0110 01112.
При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.
Например, переведем троичное число 2113 в семеричную систему счисления. Для этого сначала преобразуем число 2113 в десятичное, записав его развернутую форму:
2113 = 2 ⋅ 3 2 + 1 ⋅ 3 1 + 1 ⋅ 3 0 = 18 + 3 + 1 = 2210.
Затем переведем десятичное число 2210 в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:
Примеры решения задач
Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.
Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.
a1 = 0; x = 5 + 0 · 8 = 5;.
a1=1; x = 5 + 1 · 8 = 13;.
a1 = 2; x = 5 + 2 · 8 = 21;.
Арифметические операции в позиционных системах счисления
Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 – 0 = 0 | 0 ⋅ 0 = 0 |
| 0 + 1 = 1 | 1 – 0 = 1 | 0 ⋅ 1 = 0 |
| 1 + 0 = 1 | 1 – 1 = 0 | 1 ⋅ 0 = 0 |
| 1 + 1 = 10 | 10 – 1 = 1 | 1 ⋅ 1 = 1 |
Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.
Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:
Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:
Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:
Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.
Например, выполним сложение восьмеричных чисел 368 и 158, а также вычитание шестнадцатеричных чисел 9С16 и 6716:
При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.
Представление чисел в компьютере
Формат с фиксированной запятой
В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно
1 ⋅ 2 7 + 1 ⋅ 2 6 + 1 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 1 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 25510.
Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.
Для п-разрядного представления диапазон будет составлять от 0 до 2 n – 1.
Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.
Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2 n − |А|.
Алгоритм получения дополнительного кода отрицательного числа:
1. Записать прямой код числа в п двоичных разрядах.
2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)
3. Прибавить единицу к полученному обратному коду.
Например, получим дополнительный код числа –201410 для шестнадцатиразрядного представления:
| Прямой код | Двоичный код числа 201410 со знаковым разрядом | 1000011111011110 |
| Обратный код | Инвертирование (исключая знаковый разряд) | 1111100000100001 |
| Прибавление единицы | 1111100000100001 + 0000000000000001 | |
| Дополнительный код | 1111100000100010 |
При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.
1) Найдем разность 1310 – 1210 для восьмибитного представления. Представим заданные числа в двоичной системе счисления:
Запишем прямой, обратный и дополнительный коды для числа –1210 и прямой код для числа 1310 в восьми битах:
| 1310 | –1210 | |
| Прямой код | 00001101 | 10001100 |
| Обратный код | — | 11110011 |
| Дополнительный код | — | 11110100 |
Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):
Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.
2) Найдем разность 810 – 1310 для восьмибитного представления.
Запишем прямой, обратный и дополнительный коды для числа –1310 и прямой код для числа 810 в восьми битах:
| 810 | –1310 | |
| Прямой код | 00001000 | 10001101 |
| Обратный код | — | 11110010 |
| Дополнительный код | — | 11110011 |
Вычитание заменим сложением:
В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:
11111011 – 00000001 = 11111010.
Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –510.
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно
А = –2 31 = –214748364810.
Максимальное положительное число равно
А = 2 31 – 1 = 214748364710.
Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.
Формат с плавающей запятой
Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.
Число в экспоненциальном формате представляется в таком виде:
$q$ — основание системы счисления;
Например, десятичное число 2674,381 в экспоненциальной форме запишется так:
Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Две последние величины определяют диапазон изменения чисел и их точность.
Определим диапазон (порядок) и точность (мантиссу) для формата чисел обычной точности, т. е. четырехбайтных. Из 32 битов 8 выделяется для хранения порядка и его знака и 24 — для хранения мантиссы и ее знака.
Найдем максимальное значение порядка числа. Из 8 разрядов старший разряд используется для хранения знака порядка, остальные 7 — для записи величины порядка. Значит, максимальное значение равно 11111112 = 12710. Так как числа представляются в двоичной системе счисления, то
Аналогично, максимальное значение мантиссы равно
Кодирование текстовой информации. Кодировка ASCII. Основные используемые кодировки кириллицы
Соответствие между набором символов и набором числовых значений называется кодировкой символа. При вводе в компьютер текстовой информации происходит ее двоичное кодирование. Код символа хранится в оперативной памяти компьютера. В процессе вывода символа на экран производится обратная операция — декодирование, т. е. преобразование кода символа в его изображение.
Присвоенный каждому символу конкретный числовой код фиксируется в кодовых таблицах. Одному и тому же символу в разных кодовых таблицах могут соответствовать разные числовые коды. Необходимые перекодировки текста обычно выполняют специальные программы-конверторы, встроенные в большинство приложений.
Как правило, для хранения кода символа используется один байт (восемь битов), поэтому коды символов могут принимать значение от 0 до 255. Такие кодировки называют однобайтными. Они позволяют использовать 256 символов ( N = 2 I = 2 8 = 256 ). Таблица однобайтных кодов символов называется ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией). Первая часть таблицы ASCII-кодов (от 0 до 127) одинакова для всех IBM-PC совместимых компьютеров и содержит:
Вторая часть таблицы (коды от 128 до 255) бывает различной в различных компьютерах. Она содержит коды букв национального алфавита, коды некоторых математических символов, коды символов псевдографики. Для русских букв в настоящее время используется пять различных кодовых таблиц: КОИ-8, СР1251, СР866, Мас, ISO.
В последнее время широкое распространение получил новый международный стандарт Unicode. В нем отводится по два байта (16 битов) для кодирования каждого символа, поэтому с его помощью можно закодировать 65536 различных символов ( N = 2 16 = 65536 ). Коды символов могут принимать значение от 0 до 65535.
Примеры решения задач
Пример. С помощью кодировки Unicode закодирована следующая фраза:
Я хочу поступить в университет!
Оценить информационный объем этой фразы.
Решение. В данной фразе содержится 31 символ (включая пробелы и знак препинания). Поскольку в кодировке Unicode каждому символу отводится 2 байта памяти, для всей фразы понадобится 31 ⋅ 2 = 62 байта или 31 ⋅ 2 ⋅ 8 = 496 битов.
Ответ: 32 байта или 496 битов.
Технология обработки графической и звуковой информации
Растровая графика. Растровые графические объекты и операции над ними
Растровые графические изображения формируются в процессе сканирования рисунков и фотографий, а также при использовании цифровых фото- и видеокамер. С помощью графического редактора можно создать растровое графическое изображение непосредственно на компьютере.
Растровое графическое изображение состоит из отдельных точек — пикселей, образующих строки и столбцы. Основные свойства пикселя — расположение и цвет. Значения свойств кодируются двоичным кодом и сохраняются в видеопамяти компьютера.
Качество изображения на экране монитора зависит от пространственного разрешения и глубины цвета.
Пространственное разрешение определяется как произведение количества строк изображения на количество точек в строке. Глубина цвета измеряется в битах на точку и определяет количество цветов, в которые могут быть окрашены точки изображения. Чем больше пространственное разрешение и глубина цвета, тем выше качество изображения и тем больше объем его файла. В операционных системах предусмотрена возможность выбора необходимого пользователю и технически возможного графического режима.
Растровые изображения чувствительны к масштабированию. При уменьшении изображения несколько соседних точек преобразуются в одну, поэтому теряется четкость мелких деталей изображения. При его увеличении увеличивается размер каждой точки и появляется ступенчатый эффект (пикселизация изображения).
Например, для черно-белого изображения палитра состоит из двух цветов. Тогда с помощью этой формулы можно вычислить, какое количество информации необходимо, чтобы закодировать цвет каждой точки: 2 = 2 I ⇒ 2 1 = 2 I ⇒ I = 1 бит.
Информационный объем IП требуемой видеопамяти рассчитывается по формуле I п = I · X · Y,
где I — глубина цвета в битах на точку,
Х — количество точек изображения по горизонтали,
Y — количество точек изображения по вертикали.
Для кодирования цветов изображения в компьютере используются цветовые модели. Цветовая модель (система цветопередачи) — это способ представления различных цветов спектра в виде набора числовых характеристик определенных базовых компонентов.
Цветовая модель RGB. С экрана монитора человеческий глаз воспринимает цвет как сумму излучения трех базовых цветов: красного (Red), зеленого (Green) и синего (Blue). Эти цвета называются основными. Цвета палитры RGB формируются путем сложения базовых цветов, имеющих различную интенсивность. Цвет Color в палитре можно определить с помощью формулы Color = R + G + B.
Если все базовые цвета имеют максимальную интенсивность, получается белый цвет, если минимальную — черный. Серый цвет — промежуточный между черным и белым. В нем есть все цветовые составляющие, но они одинаковы и нейтрализуют друг друга. Красный цвет получается при максимальной интенсивности красного и минимальной интенсивности зеленого и синего цветов. Аналогично, зеленый и синий цвета получаются при максимальной интенсивности соответствующего базового цвета и минимальной интенсивности остальных цветов. При глубине цвета в 24 бита (трехбайтная кодировка) значение интенсивности каждого базового компонента задается целым десятичным числом от 0 до 255 или двоичным числом от 00000000 до 11111111. В этом случае красный цвет, например, будет закодирован последовательностью 255 0 0 (или 11111111 00000000 00000000); белый — 255 255 255 (11111111 11111111 11111111); желтый — 255 255 0 (или 11111111 11111111 00000000); голубой — 0 255 255 (или 00000000 11111111 11111111); черный — 0 0 0 (или 00000000 00000000 00000000). Последовательности 127 0 0 и 235 0 0 будут означать оттенки красного цвета, но в первом случае цвет будет более темный. Данная цветовая модель используется для компьютерных изображений, предназначенных для просмотра на экране монитора или телевизора.
Цветовая модель CMYK. Палитра цветов формируется путем наложения базовых цветов: голубого (Cyan), пурпурного (Magenta), желтого (Yellow) и черного (Black). Доля каждого базового компонента задается в процентах (целым числом от 0 до 100). Цвет Color в палитре можно определить с помощью формулы Color = C + M + Y.
Голубой, пурпурный и желтый цвета называются дополнительными, т. к. они дополняют основные цвета до белого: голубой дополняет красный, пурпурный — зеленый, а желтый — синий.
Данная палитра используется при печати изображений на принтере и основана на восприятии отражаемого света. Изображение на бумаге человек воспринимает в отраженном свете. Если на бумагу краски не нанесены, то падающий белый свет полностью отражается, и мы видим белый лист бумаги (White = (C = 0, M = 0, Y = 0)). Если краски нанесены, то они поглощают определенные цвета. Цвета в палитре формируются путем вычитания из белого цвета определенных цветов. Например, нанесенная на бумагу голубая краска поглощает красный свет и отражает зеленый и синий (Cyan = W – R = G + B); желтая краска поглощает синий свет и отражает красный и зеленый (Yellow = W – B = G + R).
Цветовая модель HSB. Палитра цветов формируется путем установки значений трех базовых компонентов: оттенка (Hue), насыщенности (Saturation) и яркости (Brightness). Оттенок Н определяет цвет в спектре и задается целым числом от 0 до 360 (0 — красный цвет, 360 — фиолетовый). Насыщенность S характеризует долю белого цвета, добавленного к выбранному оттенку, и задается в процентах от 0 до 100. При минимальной насыщенности какой-либо оттенок цвета становится серым. Яркость В определяется примесью черного цвета к выбранному оттенку и задается в процентах от 0 до 100. Любой оттенок при минимальной яркости становится черным. Эту модель используют художники при создании компьютерных изображений, моделируя нужный цвет на «виртуальном мольберте» графического редактора.
Форматы растровых графических файлов
При сохранении графического изображения на внешнем носителе могут использоваться различные способы упорядочивания данных в файле, каждый из которых определяет формат (тип) графического файла.
За счет большого количества пикселей в изображении и соответственно большого количества данных, которые надо сохранять, размеры файлов растровых изображений достаточно велики. Поэтому для растровых графических файлов применяется сжатие. Алгоритм сжатия включается непосредственно в формат графического файла.
BMP (Bit MaP image) — универсальный формат растровых графических файлов. Изображение в этом формате сохраняется попиксельно, без сжатия. Стандартное расширение имени файла — bmp. Этот формат поддерживается многими графическими редакторами и рекомендуется для хранения и обмена данными с другими приложениями.
JPEG (Joint Photographic Expert Group) — использует эффективные алгоритмы сжатия данных, которые значительно уменьшают размеры файлов. Но это достигается за счет необратимой потери части данных и ухудшения качества изображения. Стандартные расширения имени файла — jpg или jpeg. Данный формат целесообразно использовать для хранения многоцветных изображений с плавными переходами между цветами, где потеря качества малозаметна. Формат поддерживается приложениями для различных операционных систем и часто используется для размещения графических изображений на Web-страницах в Интернете.
GIF (Graphics Interchange Format) — самый «плотный» из графических форматов, не имеющих потери информации. Файлы этого формата имеют расширение gif. В этом формате хранятся и передаются малоцветные (до 256 цветов) изображения, например рисованные иллюстрации. У этого формата есть интересные особенности, позволяющие создавать необычные эффекты: прозрачность фона и анимацию изображения.
TIFF (Tagged Image File Format) — формат, поддерживаемый всеми основными графическими редакторами, включает в себя алгоритм сжатия без потерь информации. Файлы этого формата имеют расширение tif. Они сохраняют изображения с высоким качеством, поэтому широко используются в полиграфии. Формат обеспечивает не очень большую степень сжатия, но дает возможность сохранять в одном файле дополнительную информацию в невидимых вспомогательных слоях — каналах (например, наложение аннотаций и примечаний на рисунок).
PNG (Portable Network Graphic) — формат, аналогичный формату GIF, но позволяет использовать значительно больше цветов в изображении. Стандартное расширение имени файла — png.
Существуют и другие форматы растровых файлов, такие как PCX, IFF, LBM, IMG, MAC, MSP, PGL.
Среди всего разнообразия форматов нет идеального, удовлетворяющего всем требованиям пользователя. Поэтому графические редакторы предоставляют пользователю возможность самостоятельно выбирать формат графического файла в зависимости от целей работы с ним и последующего использования.
Для создания, редактирования и просмотра графических изображений используются специальные программы — графические редакторы.
С помощью растровых графических редакторов можно обрабатывать цифровые фотографии и отсканированные изображения, повышая при этом их качество путем изменения яркости, контрастности, цветовой палитры, а также удаления дефектов изображения. Кроме того, растровые графические редакторы позволяют создавать новые изображения и применять к ним различные эффекты преобразования. Необходимо помнить, что после окончания рисования нарисованный объект перестает существовать как самостоятельный элемент и становится лишь группой пикселей на рисунке.
Существуют простые растровые графические редакторы, например Paint — стандартное приложение операционной системы Windows, и мощные графические системы, например Adobe Photoshop. Основные возможности растровых графических редакторов:
— определение области рисования (размер, поля, ориентация холста);
— рисование стандартных графических примитивов (линии, прямоугольники, многоугольники, овалы);
— рисование традиционными методами с помощью инструментов рисования, таких как карандаш, кисть, распылитель, заливка, ластик;
— добавление текста и его форматирование;
— управление цветом: выбор цвета из стандартной и расширенной палитры, копирование цвета, определение цвета пикселя;
— выделение области изображения для обработки специальными инструментами;
— копирование, перемещение, удаление выделенных областей изображения;
— геометрическое преобразование выделенных областей изображения: изменение размера, поворот, наклон, отражение.
Примеры решения задач
Пример 1. В процессе преобразования растрового графического изображения количество цветов уменьшилось с 65536 до 16. Как уменьшился его информационный объем?
2 I2 = 16; 2 I2 = 2 4 ⇒ I2 = 4.
Ответ: информационный объем уменьшился в 4 раза.
Решение. В палитре 2 цвета, следовательно, глубина цвета I = 1 бит (2 = 2 I ; 2 1 = 2 I ⇒ I = 1).
Информационный объем IП найдем по формуле: IП = I · X · Y = 1 · 10 · 10 = 100 битов.
Решение. По условию IП =1,5 Кбайт или 1,5 · 2 10 байт = 1,5 · 2 10 · 8 бит.
Из формулы N = 2 I найдем число цветов N: N = 2 3 = 8 цветов.
Ответ: максимально возможное количество цветов в палитре — 8.
Пример 5. Каков минимальный объем памяти, достаточный для хранения любого растрового изображения размером 256 × 256 пикселей, если в изображении используется палитра из 216 цветов? (Саму палитру хранить не нужно).
Решение. Из формулы N = 2 I найдем глубину цвета I: 2 16 = 2 I ; I = 16. Тогда объем памяти IП = I · X · Y = 16 · 256 · 256 = 2 4 · 2 8 · 2 8 = 2 20 бита = 2 20 : 8 = 2 17 байта = 2 7 Кбайтт.
Ответ: 2 7 Кбайт = 128 Кбайт.
Векторная графика. Векторные графические объекты и операции над ними
В векторной графике основным элементом изображения является линия. В растровой графике тоже существует линия, но там она рассматривается как комбинация точек. Для каждой точки отводится одна или несколько ячеек памяти. Следовательно, чем длиннее растровая линия, тем больше памяти она занимает. В векторной графике объем памяти, занимаемый линией, не зависит от размеров линии, поскольку линия представляется в виде нескольких параметров. Что бы мы ни делали с этой линией, меняются только ее параметры, хранящиеся в ячейках памяти. Количество же ячеек остается неизменным для любой линии.
Линия — это элементарный объект векторной графики. Простейшие объекты объединяются в более сложные. Например, объект четырехугольник можно рассматривать как четыре связанные линии, а объект куб — либо как 12 связанных линий, либо как 6 связанных четырехугольников. Из-за такого подхода векторную графику часто называют объектно-ориентированной графикой.
Как и все объекты, линии имеют свойства: форма линии, ее толщина, цвет, характер линии (сплошная, пунктирная и т. п.). Замкнутые линии имеют свойство заполнения. Внутренняя область замкнутого контура может быть заполнена цветом, текстурой, картой. Незамкнутая линия имеет вершины, которые называются узлами. Узлы тоже имеют свойства, от которых зависит, как выглядит вершина линии и как две линии сопрягаются между собой.
Хотя объекты векторной графики хранятся в памяти в виде набора параметров, на экран все изображения все равно выводятся в виде точек. Перед выводом на экран каждого объекта программа производит вычисления координат экранных точек в изображении объекта. Аналогичные вычисления производятся и при выводе объектов на принтер.
Достоинства векторной графики:
Программы, предназначенные для работы с векторными изображениями, называют векторными графическими редакторами. Их применяют в тех случаях, когда основным требованием к изображению является высокая точность формы. Такая задача возникает при разработке логотипов компаний, при художественном оформлении текста (например, журнальных заголовков или рекламных объявлений), а также во всех случаях, когда иллюстрация является чертежом, схемой или диаграммой, а не рисунком. Векторная графика также лежит в основе flash-анимации. Примеры редакторов: Adobe Illustrator, Macromedia Freehand, CorelDraw.
Основные возможности векторных графических редакторов:
1) создание изображения:
2) редактирование изображения:
Форматы векторных графических файлов
Разнообразие форматов векторной графики значительно меньше, чем растровой графики, и практически каждый векторный редактор использует свой собственный формат сохранения данных.
WMF (Windows MetaFile) — универсальный формат векторных графических файлов для приложений Windows. Используется для хранения коллекции графических изображений Microsoft Clip Gallery. Возможные расширения файлов WMF, EMF, WMZ, EMZ:
CGM (Computer Graphic Metafile) — широко используется как стандартный формат векторных графических данных в сети Интернет.
EPS (Encapsulated PostScript) — формат, поддерживаемый программами для различных операционных систем. Рекомендуется для создания иллюстраций в настольных издательских системах.
CDR (CorelDRaw files) — оригинальный формат файлов векторного графического редактора CorelDraw. Изображение в файле может состоять из нескольких страниц. Формат позволяет сохранять не только векторную графику, но и текст и растровые изображения. Максимальный размер рисунка 45 × 45 м. Возможные расширения файлов CDR или CDТ.
AI (Adobe Illustrator files) — оригинальный формат файлов векторного графического редактора Adobe Illustrator. Сохраняет в файле только одну страницу, максимальный размер рисунка 3 × 3 м.
SVG (Scalable Vector Graphics) — универсальный формат двумерной графики. Позволяет сохранять в файле текст, графические изображения и анимацию. Файлы могут дополнительно сжиматься программами-архиваторами. Формат обрабатывается практически всеми векторными графическими редакторами. Широкое применение получил в инженерной графике и при разработке Web-сайтов.
Компьютерное черчение
Системы компьютерного черчения являются векторными редакторами, предназначенными для создания чертежей. Они позволяют создавать чертежи с высокой точностью, а также измерять расстояния, углы, периметры и площади начерченных объектов. Системы компьютерного черчения используются в качестве инструментов автоматического проектирования на производстве.
Примером системы автоматизированного проектирования является система КОМПАС-3D. В центре рабочего окна расположена система координат, от начала которой отсчитывается положение курсора. Создание и редактирование чертежа реализуется с помощью инструментальной панели, содержащей пять функциональных групп инструментов:
Создание чертежного объекта осуществляется щелчком мыши на соответствующей кнопке панели Геометрические построения. После этого на экране появится Строка параметров объекта с полями для задания значений, которые характеризуют размеры объекта и его положение на чертеже. При редактировании объектов в Строке параметров объекта активизируют нужные поля и вводят новые значения.
Кроме ручного ввода значений параметров объектов в Строку параметров, можно осуществлять автоматический ввод параметров (активизацией поля и щелчком мыши в нужном месте чертежа) и ввод параметров с использованием геометрического калькулятора (значение параметров объекта определяется на основе параметров другого, указанного мышью объекта).
Создание и редактирование цифровых звукозаписей
Звук — это продольная волна сжатия/расширения, распространяющаяся в воздушной, водной или другой среде (механические колебания). Звук характеризуется интенсивностью, которую человек воспринимает как громкость, и частотой, воспринимаемой как тон. Чем больше интенсивность, тем громче звук; чем выше тон, тем выше частота.
Диапазон частот звука, воспринимаемых человеком, очень велик (от 20 Гц до 20000 Гц). Для измерения интенсивности (мощности) звука используются относительные логарифмические единицы — децибелы. Изменение мощности звука в 10 раз соответствует изменению на 10 децибел. Разность между максимальной и минимальной интенсивностью звука называется динамическим диапазоном, и для человеческого уха она составляет огромную величину — 140 децибел.
Для преобразования звуковых колебаний в электрические применяют микрофоны. Чтобы микрофон можно было подключить к компьютеру, компьютер должен быть оборудован звуковой картой. В последнее время звуковые карты интегрированы в материнские платы, однако лучшее качество обеспечивают дискретные и внешние карты.
Звуковая волна по своей природе непрерывна. Для ее обработки в компьютере производится дискретизация по времени и по уровню. В результате этого процесса непрерывная волна заменяется совокупностью цифровых отсчетов громкости сигнала в дискретные равноотстоящие моменты времени. Эту задачу выполняет АЦП (аналогово-цифровой преобразователь) звуковой карты. Чем больше разрядность АЦП, тем точнее передается форма звуковой волны, тем меньше искажения и тем больше динамический диапазон.
От быстродействия АЦП зависит максимальная частота записываемого звука. Минимальное значение частоты дискретизации по теореме Котельникова должно вдвое превышать максимально возможную частоту записываемого сигнала. Например, цифровой компакт-диск имеет два канала записи с частотой дискретизации 44100 Гц и 16-битное кодирование. При этом гарантируется частотный диапазон записи до 20000 Гц; динамический диапазон теоретически может достигать 90 децибел. Одна секунда записи компакт-диска займет 2 ⋅ 2 ⋅ 44100 = 176400 байтов. Одна минута — 10,1 Мбайт.
Для современных звуковых карт частота дискретизации может быть от 6 до 192 кГц, кодирование — 8, 16 или 32 бита.
Прямая запись звуковой волны приводит к большим объемам файлов. Поэтому для аудиофайлов было изобретено множество форматов. Они делятся на форматы без потери качества (lossless) и с потерей качества (lossy).
К lossless-форматам относятся WAV, APE, FLAC. В них сжатие или не применяется совсем, или применяется обратимое (архивация).
В lossy-форматах (MP3, OGG, WMA и т. д.) кроме архивации применяется психоакустическое кодирование, использующее физиологические свойства человеческого слуха, такие как маскировка более слабого сигнала более сильным и т. п. При этом ради достижения большего сжатия из сигнала выбрасывается часть информации и его полное восстановление становится невозможным.
Для создания и редактирования цифровых звукозаписей применяются специальные программы — звуковые редакторы, например Adobe Audition, Sound Forge. Они позволяют не только записывать, воспроизводить и синтезировать звук, но и проводить его сложную обработку. Нелинейный монтаж, реставрация, акустические эффекты, а также музыкальные преобразования (изменение тональности и темпа) выполняются наглядно и просто — несколькими щелчками мыши. Эта видимая простота и наглядность в своей основе имеют очень сложные математические алгоритмы спектрального анализа, в частности быстрое преобразование Фурье, статистической обработки сигналов и т. д.
Современные звуковые редакторы позволяют записывать аудиофайлы в различных форматах в зависимости от того, как они далее будут использованы (на чем будут воспроизведены). Чтобы звук попал в компьютер, необходимо подключить источник сигнала к звуковой карте. Например, микрофон — к микрофонному входу, или другой источник — к линейному входу звуковой карты. Далее необходимо настроить звуковую карту, т. е. выбрать источник и уровень сигнала. Для этого используется стандартная программа Регулятор громкости, входящая в состав операционной системы Windows. При выборе команды Параметры/Свойства откроется окно Свойства, в котором нужно включить переключатель Запись, указать нужный вход (Microphone или Line-in) и установить необходимый уровень записи. Далее можно использовать любой звуковой редактор. При использовании звуковых редакторов новый файл создается традиционной командой File/New. При этом потребуется установить частоту дискретизации и глубину кодирования звукового сигнала, а также режим записи (стерео или моно). Для музыкального сигнала лучше использовать параметры компакт-диска (44100 Гц, 16 битов, два канала); если требования к качеству звука выше, можно поднять частоту дискретизации до 48000 Гц. Речь с микрофона в нестудийных условиях с приемлемым качеством можно писать и с частотой дискретизации 8000 Гц, 8 битов, 1 канал. Дальнейшие действия выполняются в соответствии с инструкцией к конкретному редактору.
Для того чтобы прослушать звуковой файл, нужно к линейному выходу звуковой карты подключить колонки или наушники. Сравнительно недавно появились компьютерные колонки со встроенным ЦАП (цифро-аналоговым преобразователем), питание и сигнал в которые подается через шину USB. В этом случае можно воспроизводить аудиофайлы на компьютере без звуковой карты. Компьютерный звук воспроизводится специальной программой-плеером, которая управляет ЦАП звуковой карты. В состав операционной системы Windows входит стандартный проигрыватель Windows Media Player; из аналогичных продуктов других фирм очень популярна программа WinAmp. Эти программы позволяют воспроизводить аудиофайлы практически любого формата.
Компьютерные презентации: типы слайдов, мультимедиа эффекты, организация переходов между слайдами
Компьютерные презентации являются одним из типов мультимедийных проектов. Презентация — ряд последовательно демонстрируемых в процессе урока, лекции, конференции, совещания и т. д. изображений — слайдов, содержащих текстовую и графическую информацию.
Графическая программа PowerPoint нашла широкое применение как средство создания презентаций. Она предоставляет возможность пользователю самостоятельно создавать слайды, вносить изменения, дополнять текстовые и графические элементы, а также редактировать всю презентацию в целом. Данная программа позволяет наглядно представить сообщение несколькими способами: показом слайдов на экране, на бумажной распечатке или пленке для проектора (35 мм), размещением в Интернете на одной или нескольких страницах или демонстрацией с компакт-диска. PowerPoint может задействовать элементы, полученные из множества источников. Создавая слайды, можно не только использовать встроенные в программу инструменты, но и импортировать элементы из других программ.
Порядок создания презентации в программе PowerPoint из пакета Microsoft Office 2007
Основные типы слайдов
Текстовые слайды. К ним относятся заголовки, маркированные списки и текст в две колонки. В слайдах других видов текст комбинируется с такими элементами, как картинки, диаграммы или видеоклипы. На ленте появляется дополнительная панель Средства рисования с вкладкой Фор- мат, команды которой позволяют отформатировать текст: задать стиль, цвет контура и заливки, добавить эффекты (тень, отражение, рельеф и др.), выровнять или развернуть текст, изменить его размер и переместить на задний или передний план.
Слайды с диаграммами. В PowerPoint можно создавать разнообразные двумерные и трехмерные диаграммы. Диаграммы, имеющие оси, создаются для того, чтобы продемонстрировать относительные величины и взаимосвязи между несколькими классами (например, нужно сравнить продажи текущего и прошлого года или выяснить, скорость какого процессора выше, и т. д.). Круговые диаграммы позволяют определить долю составляющего от целого. При добавлении на слайд диаграммы на ленте появляется дополнительная панель Работа с диаграммами, содержащая вкладки Конструктор, Макет и Формат.
Слайды с таблицами. При активизации таблицы на ленте появляется дополнительная панель Работа с таблицами, содержащая вкладки Конструктор и Макет, команды которых позволяют настроить внешний вид таблицы и ее структуру.
Слайды с рисунками. На слайд можно поместить предлагаемые программой образцы изображений или рисунок из любого файла пользователя, причем изображение можно как внедрить в документ, так и связать с файлом. На ленте появляется дополнительная панель Работа с рисунками, содержащая вкладку Формат.
Чтобы начать показ слайдов, надо нажать клавишу [F5]. Слайд появится в полноэкранном режиме. Для перехода к следующему слайду надо нажать клавишу [Enter] или левую кнопку мыши. Нажатие [Esc] отменяет показ слайдов. Во время показа презентации можно перейти к любому слайду. Для этого надо щелкнуть в любом месте слайда правой кнопкой мыши и в появившемся контекстном меню выбрать команду Перейти к слайду.
Во время показа слайдов может возникнуть необходимость сделать пометки на слайде, чтобы подчеркнуть какую-либо мысль. Для этого во время показа надо вызвать контекстное меню и выбрать в нем команду Указатель. В появившемся окне можно выбрать вид указателя (стрелка, ручка, фломастер, выделение), и при движении мыши на слайде будет создаваться рисунок.
PowerPoint позволяет задать автоматический показ слайдов (без щелчков мышью для перехода к следующему слайду). Можно предварительно отрепетировать показ презентации. По команде Настройка времени из группы Настройка вкладки Показ слайдов на экране появится первый слайд и откроется панель инструментов Репетиция. Теперь нужно отрепетировать свою речь при отображении каждого слайда. Когда вы будете готовы перейти к следующему слайду, надо нажать любую из клавиш, выполняющих эту функцию, или щелкнуть на кнопке Далее панели инструментов Репетиция. Те же действия надо выполнять на протяжении всего показа слайдов. После окончания программа отобразит общее время показа и задаст вопрос, сохранить ли время смены для каждого слайда и использовать ли его при показе презентации. Щелчок на кнопке Да запишет время и создаст автоматический показ слайдов.