Машина Тьюринга: описание и примеры машин Тьюринга
Что это и кто создал
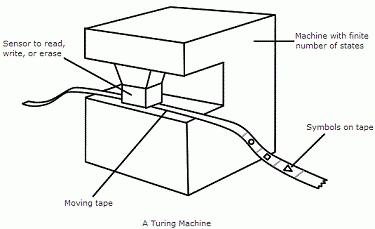
Алан Тьюринг стремился описать наиболее примитивную модель механического устройства, которая имела бы те же основные возможности, что и компьютер. Тьюринг впервые описал машину в 1936 году в статье «О вычислимых числах с приложением к проблеме разрешимости», которая появилась в Трудах Лондонского математического общества.
Из чего состоит устройство
Каждая такая машина состоит из двух составляющих:
Как работает механизм
Машина Тьюринга имеет принципиальное отличие от вычислительных устройств – ее запоминающее приспособление имеет бесконечную ленту, тогда как у цифровых аппаратов такое устройство имеет полосу определенной длины. Каждый класс заданий решает только одна построенная машина Тьюринга. Задачи иного вида предполагают написание нового алгоритма.
Управляющее устройство, находясь в одном состоянии, может передвигаться в любую сторону по ленте. Оно записывает в ячейки и считывает с них символы конечного алфавита. В процессе перемещения выделяется пустой элемент, который заполняет позиции, не содержащие входные данные. Алгоритм для машины Тьюринга определяет правила перехода для управляющего устройства. Они задают головке записи-чтения такие параметры: запись в ячейку нового символа, переход в новое состояние, перемещение влево или вправо по ленте.
Свойства механизма
Машина Тьюринга, как и другие вычислительные системы, имеет присущие ей особенности, и они сходны со свойствами алгоритмов:
Функции машины Тьюринга
В решении алгоритмов часто требуется реализация функции. В зависимости от возможности написания цепочки для вычисления, функцию называют алгоритмически разрешимой или неразрешимой. В качестве множества натуральных или рациональных чисел, слов в конечном алфавите N для машины рассматривается последовательность множества В – слова в рамках двоичного кодового алфавита В=<0.1>. Также в результат вычисления учитывается «неопределенное» значение, которое возникает при «зависании» алгоритма. Для реализации функции важно наличие формального языка в конечном алфавите и решаемость задачи распознавания корректных описаний.
Программа для устройства
Составляющие для вычислений
Чтобы построить машину Тьюринга для решения одной определенной задачи, необходимо определить для нее следующие параметры.
Непрерывная цепочка букв-символов, записываемая на ленту, именуется словом.
Таблица переходов. Эта составляющая представляет собой алгоритм поведения каретки устройства в зависимости от того, каковы в данный момент состояние автомата и значение считываемого символа.
Алгоритм для автомата
Кареткой устройства Тьюринга во время работы управляет программа, которая во время каждого шага выполняет последовательность следующих действий:
Машина Тьюринга: примеры
Пример 1. Дана задача построить алгоритм, прибавляющий единицу к последней цифре заданного числа, расположенного на ленте. Входные данные – слово – цифры целого десятичного числа, записанные в последовательные ячейки на ленту. В первоначальный момент устройство располагается напротив самого правого символа – цифры числа.
Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:
| a0 | 0 | 1 | 2 | 3 | . | 7 | 8 | 9 | |
| q1 | 1 H q0 | 1 H q0 | 2 H q0 | 3 H q0 | 4 H q0 | . | 8 H q0 | 9 H q0 | 0 λ q1 |
Здесь q1 — состояние изменения цифры, q0 — остановка. Если в q1 автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q0, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q1. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q0 – остановка.
| a0 | ( | ) | |
| q1 | a0 H q0 | ( П q2 | ) П q1 |
| q2 | a0 H q0 | ( П q2 | ) λ q3 |
| q3 | a0 H q0 | a0 П q3 | a0 П q1 |
Состояние q1: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q2; если определен “a0”, то остановка.
Состояние q2: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q3.
Состояние q3: осуществить удаление сначала символа “(”, а затем “)” и перейти в q1.
Машина Тьюринга
Вы будете перенаправлены на Автор24
Машина Тьюринга — это абстрактный исполнитель или абстрактная вычислительная машина.
Введение
Машина Тьюринга является одним из наиболее выдающихся научных изобретений двадцатого века. Она представляла несложную и удобную абстрактную модель вычислительного процесса, которая представлена в обобщённом формате и позволяет реализовать практически все компьютерные задачи. Простое описание и выполненный математический анализ позволяют считать её фундаментом теоретической информатики.
Эта научная работа послужила стимулом к более углублённому изучению цифрового исчисления и компьютерных устройств, в том числе осознание мысли, что есть проблематика в сфере вычислений, которую нельзя решить на обычных электронных вычислительных машинах пользователей
Машина Тьюринга
Алан Тьюринг хотел выполнить описание самой простой модели механического модуля, который обладал бы такими же базовыми возможностями, как и компьютер. Первое описание такой машины Тьюринг опубликовал в 1936-ом году в работе с названием «О вычислимых числах в приложении к проблеме разрешения», появившейся в работах Лондонского математического сообщества.
Машина Тьюринга была вычислительным модулем, который состоит из сканера для чтения и записи информации с бумажной ленты, пропускаемой через него. Лента поделена на квадратики, несущие один знак, а именно нуль или единицу. Механизм предназначен для ввода и вывода информации и одновременно служит рабочей памятью для сохранения итогов промежуточных вычислительных шагов. Машина имеет в своём составе два компонента:
Готовые работы на аналогичную тему
Принцип работы машины Тьюринга
Машина Тьюринга принципиально отличается от компьютерных модулей, у неё в качестве запоминающего устройства выступает бесконечная лента, а у цифровых устройств память представляет полосу заданной длины. Любой тип заданий может решить лишь одна сформированная машина Тьюринга. Задания другого класса могут быть решены написанием другого алгоритма. Устройство управления находится в определённом состоянии и способно перемещаться в обе стороны вдоль ленты. Оно может записывать в ячейки и считывать из них алфавитные символы. При перемещении определяется пустой компонент, заполняющий места, которые не содержать входных данных. Алгоритм машины Тьюринга формирует условия перемещений управляющего механизма. Он может задать головке, выполняющей запись и чтение данных, следующие команды:
Машина Тьюринга подобно другим системам, предназначенным для вычислений, обладает определёнными особенностями, которые похожи на свойства алгоритмов:
Функции машины Тьюринга
Рисунок 1. Функции машины Тьюринга. Автор24 — интернет-биржа студенческих работ
Программа для машины Тьюринга
Программа для машины Тьюринга формируется как таблицы, в которых в первой строчке и столбце находятся знаки внешнего алфавита и набор допустимых внутренних состояний автомата, то есть внутренний алфавит. Данные в таблице, по сути, это команды, которые должна исполнять машина Тьюринга. Разрешение задачи выполняется по следующим правилам. Символ, принятый сканером из ячейки, над которой он располагается в текущий момент, и определённое внутреннее состояние сканера автомата определяют, какую команду требуется исполнить. А именно, это команда, расположенная в таблице, и находящаяся в точке пересечения знаков внутреннего и внешнего алфавита.
Характеристика машины Тьюринга
Понятие и формальное описание машины Тьюринга, ее свойства (дискретность, понятность, детерминированность, массовость) и программная реализация. Параметры вычислительной сложности алгоритма. Причины, ведущие к алгоритмической неразрешимости проблем.
| Рубрика | Программирование, компьютеры и кибернетика |
| Вид | курсовая работа |
| Язык | русский |
| Дата добавления | 01.10.2012 |
| Размер файла | 84,2 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
1. Описание машины Тьюринга
1.1 Свойства машины Тьюринга как алгоритма
2. Сложность алгоритмов
2.1 Сложность проблем
3. Машина Тьюринга и алгоритмически неразрешимые проблемы
4. Реализация машины Тьюринга
Устройство машины Тьюринга чрезвычайно просто, однако на ней можно выполнить практически любую программу. Для выполнения всех этих действий предусмотрена специальная таблица правил, в которой прописано, что нужно делать при различных комбинациях текущих состояний и символов, прочитанных с ленты.
В 1947 г. Алан Тьюринг расширил определение, описав «универсальную машину Тьюринга». Позже для решения определенных классов задач была введена ее разновидность, которая позволяла выполнять не одну задачу, а несколько.
1. Описание машины Тьюринга
Алан Тьюринг (Turing) в 1936 году опубликовал в трудах Лондонского математического общества статью «О вычислимых числах в приложении к проблеме разрешения», которая наравне с работами Поста и Черча лежит в основе современной теории алгоритмов.
Приведем характеристику этой работы, принадлежащую Джону Хопкрофту: «Работая над проблемой Гильберта, Тьюрингу пришлось дать четкое определение самого понятия метода. Отталкиваясь от интуитивного представления о методе как о некоем алгоритме, т.е. процедуре, которая может быть выполнена механически, без творческого вмешательства, он показал, как эту идею можно воплотить в виде подробной модели вычислительного процесса. Полученная модель вычислений, в которой каждый алгоритм разбивался на последовательность простых, элементарных шагов, и была логической конструкцией, названной впоследствии машиной Тьюринга».
Машина Тьюринга является расширением модели конечного автомата, расширением, включающим потенциально бесконечную память с возможностью перехода (движения) от обозреваемой в данный момент ячейки к ее левому или правому соседу.
Формально машина Тьюринга может быть описана следующим образом. Пусть заданы:
один символ из Г—>е (пустой);
Остановка машины происходит в том случае, если для пары (qi,Si) функция перехода не определена.
Алан Тьюринг высказал предположение, что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной Тьюринга. Это предположение известно как тезис Черча-Тьюринга. Каждый компьютер может моделировать машину Тьюринга (операции перезаписи ячеек, сравнения и перехода к другой соседней ячейке с учетом изменения состояния машины). Следовательно, он может моделировать алгоритмы в любом формализме, и из этого тезиса следует, что все компьютеры (независимо от мощности, архитектуры и т.д.) эквивалентны с точки зрения принципиальной возможности решения алгоритмических задач.
1.1 Свойства машины Тьюринга как алгоритма
На примере машины Тьюринга хорошо прослеживаются свойства алгоритмов. Попросите учащихся показать, что машина Тьюринга обладает всеми свойствами алгоритма.
Понятность. На каждом шаге в ячейку пишется символ из алфавита, автомат делает одно движение (Л, П, Н), и машина Тьюринга переходит в одно из описанных состояний.
Детерминированность. В каждой клетке таблицы машины Тьюринга записан лишь один вариант действия. На каждом шаге результат определен однозначно, следовательно, последовательность шагов решения задачи определена однозначно, т.е. если машине Тьюринга на вход подают одно и то же входное слово, то выходное слово каждый раз будет одним и тем же.
Результативность. Содержательно результаты каждого шага и всей последовательности шагов определены однозначно, следовательно, правильно написанная машина Тьюринга за конечное число шагов перейдет в состояние q0, т.е. за конечное число шагов будет получен ответ на вопрос задачи.
Массовость. Каждая машина Тьюринга определена над всеми допустимыми словами из алфавита, в этом и состоит свойство массовости. Каждая машина Тьюринга предназначена для решения одного класса задач, т.е. для каждой задачи пишется своя (новая) машина Тьюринга.
2. Сложность алгоритмов
Обычно вычислительная сложность алгоритма выражается с помощью нотации «О большого», т. е описывается порядком величины вычислительной сложности. Это просто член разложения функции сложности, быстрее всего растущий с ростом n, все члены низшего порядка игнорируются. Например, если временная сложность данного алгоритма равна 4n2+7n+12, то вычислительная сложность порядка n2, записываемая как О(n2).
Временная сложность измеренная таким образом не зависит от реализации. Не нужно знать ни точное время выполнения различных инструкций, ни число битов, используемых для представления различных переменных, ни даже скорость процессора. Один компьютер может быть на 50 процентов быстрее другого, а у третьего шина данных может быть в два раза шире, но сложность алгоритма, оцененная по прядку величины, не изменится. Это не жульничество, при работе с алгоритмами настолько сложными, как описанные в этой книге, всем прочим можно пренебречь (с точностью до постоянного множителя) в сравнении со сложностью по порядку величины.
Эта нотация позволяет увидеть, как объем входных данных влияет на требования к времени и объему памяти. Например, если Т= О(n), то удвоение входных данных удвоит и время выполнения алгоритма. Если Т=О(2n), то добавление одного бита к входным данным удвоит время выполнения алгоритма.
В идеале, криптограф хотел бы утверждать, что алгоритм, лучший для взлома спроектированного алгоритма шифрования, обладает экспоненциальной временной сложностью. На практике, самые сильные утверждения, которые могут быть сделаны при текущем состоянии теории вычислительной сложности, имеют форму «все известные алгоритмы вскрытия данной криптосистемы обладают суперполиномиальной временной сложностью». То есть, известные нам алгоритмы вскрытия обладают суперполиномиальной временной сложностью, но пока невозможно доказать, что не может быть открыт алгоритм вскрытия с полиномиальной временной сложностью. Развитие теории вычислительной сложности возможно когда-нибудь позволит создать алгоритмы, для которых существование алгоритмов с полиномиальным временем вскрытия может быть исключено с математической точностью.
С ростом n временная сложность алгоритмов может стать настолько огромной, что это повлияет на практическую реализуемость алгоритма.
2.1 Сложность проблем
Теория сложности также классифицирует и сложность самих проблем, а не только сложность конкретных алгоритмов решения проблемы. Теория рассматривает минимальное время и объем памяти, необходимые для решения самого трудного варианта проблемы на теоретическом компьютере, известном как машина Тьюринга. Машина Тьюринга представляет собой конечный автомат с бесконечной лентой памяти для чтения записи и является реалистичной моделью вычислений.
Проблемы, которые можно решить с помощью алгоритмов с полиномиальным временем, называются решаемыми, потому что для разумных входных данных обычно могут быть решены за разумное время. (Точное определение «разумности» зависит от конкретных обстоятельств) Проблемы, которые невозможно решить за полиномиальное время, называются нерешаемыми, потому что вычисление их решений быстро становится невозможным. Нерешаемые проблемы иногда называют трудными. Проблемы, которые могут быть решены только с помощью суперполиномиальных алгоритмов, вычислительно нерешаемы, даже при относительно малых значениях n.
Что еще хуже, Алан Тьюринг доказал, что некоторые проблемы принципиально неразрешимы. Даже отвлекаясь от временной сложности алгоритма, невозможно создать алгоритм решения этих проблем.
Задачи можно разбить на классы в соответствии со сложностью их решения. Вот важнейшие из них и предполагаемые соотношения между ними: P NP (или P=NP). Однако, большинство специалистов, занимающихся теорией сложности, убеждены, что это классы неравны.
Как ни странно, можно доказать, что некоторые NP-задачи настолько же трудны, что и любая задача этого класса. Такие задачи называются NP-полными. То есть, если такая задача решается за полиномиальное время, то P=NP.
Наконец, существует класс задач EXPTIME. Эти задачи решаются за экспоненциальное время. В настоящее время можно доказать, что EXPTIME-полные задачи невозможно решить за детерминированное полиномиальное время. Кроме того, доказано, что P<>EXPTIME.
3. Машина Тьюринга и алгоритмически неразрешимые проблемы
Имеет место быть следующая теорема: не существует алгоритма (машины Тьюринга), позволяющего по описанию произвольного алгоритма и его исходных данных (и алгоритм и данные заданы символами на ленте машины Тьюринга) определить, останавливается ли этот алгоритм на этих данных или работает бесконечно.
Таким образом, фундаментально алгоритмическая неразрешимость связана с бесконечностью выполняемых алгоритмом действий, т.е. невозможностью предсказать, что для любых исходных данных решение будет получено за конечное количество шагов.
Тем не менее, можно попытаться сформулировать причины, ведущие к алгоритмической неразрешимости, эти причины достаточно условны, так как все они сводимы к проблеме останова, однако такой подход позволяет более глубоко понять природу алгоритмической неразрешимости:
а) Отсутствие общего метода решения задачи
Проблема 1: Распределение девяток в записи числа;
Задача состоит в вычислении функции f(n) для произвольно заданного n.
Проблема 2: Вычисление совершенных чисел;
Проблема 3: Десятая проблема Гильберта;
Ю.В. Матиясевич показал, что такого алгоритма не существует, т.е. отсутствует общий метод определения целых корней уравнения P=0 по его целочисленным коэффициентам.
б) Информационная неопределенность задачи
Проблема 4: Позиционирование машины Поста на последний помеченный ящик;
Пусть на ленте машины Поста заданы наборы помеченных ящиков (кортежи) произвольной длины с произвольными расстояниями между кортежами и головка находится у самого левого помеченного ящика. Задача состоит установке головки на самый правый помеченный ящик последнего кортежа.
в) Логическая неразрешимость (в смысле теоремы Гёделя о неполноте)
Проблема 5: Проблема «останова» (см. теорема);
Проблема 6: Проблема эквивалентности алгоритмов;
По двум произвольным заданным алгоритмам (например, по двум машинам Тьюринга) определить, будут ли они выдавать одинаковые выходные результаты на любых исходных данных.
Проблема 7: Проблема тотальности;
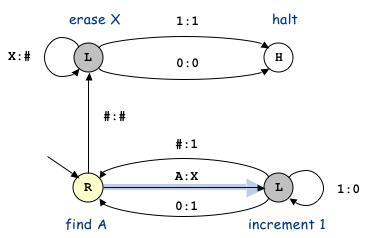
4. Реализация машины Тьюринга
Входные параметры и условия:
Дана строка «11111111», требуется определить количество единиц и если оно четное, то добавить к началу строки «i», в случае если количество нечетное, добавить «l»
Команды для выполнения задачи:
Программа считывает данные условия из файла, потом заполняет массив с командами. После чего машина встает на начало ленты и согласно командам выполняет действия над ней.
Условно программа состоит из двух частей: первая часть считывает данные из файла и заносит команды в массив, а вторая часть программы выполняет действия над исходной строкой.
Т.е. сама программа не может выполнять действий с лентой, она это делает на основании команд хранящихся в файле.
После выполнения каждой команды машина либо сдвигается влево, либо вправо, либо остается в текущем положении и переходит к выполнению следующей команды. И так до тех пор пока не получит выходной сигнал «f». После этого машина прекращает свою работу и выводит результат на экран.
Результат работы машины представлен на рисунке 1.
Рисунок 1. Результат работы машины Тьюринга
Теория сложности также классифицирует и сложность самих проблем, а не только сложность конкретных алгоритмов решения проблемы. Теория рассматривает минимальное время и объем памяти, необходимые для решения самого трудного варианта проблемы на теоретическом компьютере, известном как машина Тьюринга. Машина Тьюринга представляет собой конечный автомат с бесконечной лентой памяти для чтения записи и является реалистичной моделью вычислений.
Задачи можно разбить на классы в соответствии со сложностью их решения. Вот важнейшие из них и предполагаемые соотношения между ними: P NP (или P=NP). Однако, большинство специалистов, занимающихся теорией сложности, убеждены, что это классы неравны.
Список литературы
машина тьюринг алгоритм неразрешимость
Реферат: Машина Тьюринга
Содержание
1. Описание машины Тьюринга. 3
1.1 Свойства машины Тьюринга как алгоритма. 5
2. Сложность алгоритмов. 7
2.1 Сложность проблем… 9
3. Машина Тьюринга и алгоритмически неразрешимые проблемы… 12
Список литературы… 18
Введение
Машина Тьюринга — это очень простое вычислительное устройство. Она состоит из ленты бесконечной длины, разделенной на ячейки, и головки, которая перемещается вдоль ленты и способна читать и записывать символы. Также у машины Тьюринга есть такая характеристика, как состояние, которое может выражаться целым числом от нуля до некоторой максимальной величины. В зависимости от состояния машина Тьюринга может выполнить одно из трех действий: записать символ в ячейку, передвинуться на одну ячейку вправо или влево и установить внутреннее состояние.
Устройство машины Тьюринга чрезвычайно просто, однако на ней можно выполнить практически любую программу. Для выполнения всех этих действий предусмотрена специальная таблица правил, в которой прописано, что нужно делать при различных комбинациях текущих состояний и символов, прочитанных с ленты.
В 1947 г. Алан Тьюринг расширил определение, описав «универсальную машину Тьюринга». Позже для решения определенных классов задач была введена ее разновидность, которая позволяла выполнять не одну задачу, а несколько.
1. Описание машины Тьюринга
Алан Тьюринг (Turing) в 1936 году опубликовал в трудах Лондонского математического общества статью «О вычислимых числах в приложении к проблеме разрешения», которая наравне с работами Поста и Черча лежит в основе современной теории алгоритмов.
Предыстория создания этой работы связана с формулировкой Давидом Гильбертом на Международном математическом конгрессе в Париже в 1900 году неразрешенных математических проблем. Одной из них была задача доказательства непротиворечивости системы аксиом обычной арифметики, которую Гильберт в дальнейшем уточнил как «проблему разрешимости» — нахождение общего метода, для определения выполнимости данного высказывания на языке формальной логики.
Статья Тьюринга как раз и давала ответ на эту проблему — вторая проблема Гильберта оказалась неразрешимой. Но значение статьи Тьюринга выходило далеко за рамки той задачи, по поводу которой она была написана.
Приведем характеристику этой работы, принадлежащую Джону Хопкрофту: «Работая над проблемой Гильберта, Тьюрингу пришлось дать четкое определение самого понятия метода. Отталкиваясь от интуитивного представления о методе как о некоем алгоритме, т.е. процедуре, которая может быть выполнена механически, без творческого вмешательства, он показал, как эту идею можно воплотить в виде подробной модели вычислительного процесса. Полученная модель вычислений, в которой каждый алгоритм разбивался на последовательность простых, элементарных шагов, и была логической конструкцией, названной впоследствии машиной Тьюринга».
Машина Тьюринга является расширением модели конечного автомата, расширением, включающим потенциально бесконечную память с возможностью перехода (движения) от обозреваемой в данный момент ячейки к ее левому или правому соседу.
Формально машина Тьюринга может быть описана следующим образом. Пусть заданы:
конечное множество состояний – Q, в которых может находиться машина Тьюринга;
конечное множество символов ленты – Г;
функция δ (функция переходов или программа), которая задается отображением пары из декартова произведения Q x Г (машина находится в состоянии qi и обозревает символ gi) в тройку декартова произведения Q х Г х
один символ из Г—>е (пустой);
одно из состояний – q0 є Q является начальным состоянием машины.
Решаемая проблема задается путем записи конечного количества символов из множества Σ є Г – Si є Σ на ленту:
Остановка машины происходит в том случае, если для пары (qi,Si) функция перехода не определена.
Алан Тьюринг высказал предположение, что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной Тьюринга. Это предположение известно как тезис Черча–Тьюринга. Каждый компьютер может моделировать машину Тьюринга (операции перезаписи ячеек, сравнения и перехода к другой соседней ячейке с учетом изменения состояния машины). Следовательно, он может моделировать алгоритмы в любом формализме, и из этого тезиса следует, что все компьютеры (независимо от мощности, архитектуры и т.д.) эквивалентны с точки зрения принципиальной возможности решения алгоритмических задач.
1.1 Свойства машины Тьюринга как алгоритма
На примере машины Тьюринга хорошо прослеживаются свойства алгоритмов. Попросите учащихся показать, что машина Тьюринга обладает всеми свойствами алгоритма.
Дискретность. Машина Тьюринга может перейти к (к + 1) — му шагу только после выполнения каждого шага, т.к именно каждый шаг определяет, каким будет (к + 1) — й шаг.
Понятность. На каждом шаге в ячейку пишется символ из алфавита, автомат делает одно движение (Л, П, Н), и машина Тьюринга переходит в одно из описанных состояний.
Детерминированность. В каждой клетке таблицы машины Тьюринга записан лишь один вариант действия. На каждом шаге результат определен однозначно, следовательно, последовательность шагов решения задачи определена однозначно, т.е. если машине Тьюринга на вход подают одно и то же входное слово, то выходное слово каждый раз будет одним и тем же.
Результативность. Содержательно результаты каждого шага и всей последовательности шагов определены однозначно, следовательно, правильно написанная машина Тьюринга за конечное число шагов перейдет в состояние q0, т.е. за конечное число шагов будет получен ответ на вопрос задачи.
Массовость. Каждая машина Тьюринга определена над всеми допустимыми словами из алфавита, в этом и состоит свойство массовости. Каждая машина Тьюринга предназначена для решения одного класса задач, т.е. для каждой задачи пишется своя (новая) машина Тьюринга.
2. Сложность алгоритмов
Сложность алгоритма определяется вычислительными мощностями, необходимыми для его выполнения. Вычислительная сложность алгоритма часто измеряется двумя параметрами: Т (временная сложность) и S (пространственная сложность, или требования к памяти). И Т, и S обычно представляются в виде функций от n, где n — это размер входных данных. (Существую и другие способы измерения сложности: количество случайных бит, ширина канала связи, объем данных и т.п.)
Обычно вычислительная сложность алгоритма выражается с помощью нотации «О большого», т. е описывается порядком величины вычислительной сложности. Это просто член разложения функции сложности, быстрее всего растущий с ростом n, все члены низшего порядка игнорируются. Например, если временная сложность данного алгоритма равна 4n2+7n+12, то вычислительная сложность порядка n2, записываемая как О(n2).
Временная сложность измеренная таким образом не зависит от реализации. Не нужно знать ни точное время выполнения различных инструкций, ни число битов, используемых для представления различных переменных, ни даже скорость процессора. Один компьютер может быть на 50 процентов быстрее другого, а у третьего шина данных может быть в два раза шире, но сложность алгоритма, оцененная по прядку величины, не изменится. Это не жульничество, при работе с алгоритмами настолько сложными, как описанные в этой книге, всем прочим можно пренебречь (с точностью до постоянного множителя) в сравнении со сложностью по порядку величины.
Эта нотация позволяет увидеть, как объем входных данных влияет на требования к времени и объему памяти. Например, если Т= О(n), то удвоение входных данных удвоит и время выполнения алгоритма. Если Т=О(2n), то добавление одного бита к входным данным удвоит время выполнения алгоритма.
Обычно алгоритмы классифицируются в соответствии с их временной или пространственной сложностью. Алгоритм называют постоянным, если его сложность не зависит от n: 0(1). Алгоритм является линейным, если его временная сложность О(n). Алгоритмы могут быть квадратичными, кубическими и т.д. Все эти алгоритмы — полиномиальны, их сложность — О(m), где m — константа. Алгоритмы с полиномиальной временной сложностью называются алгоритмами с полиномиальным временем
Алгоритмы, сложность которых равна О(tf(n)), где t — константа, большая, чем 1, a f(n) — некоторая полиномиальная функция от n, называются экспоненциальными. Подмножество экспоненциальных алгоритмов, сложность которых равна О(сf(n)), где где с — константа, a f(n) возрастает быстрее, чем постоянная, но медленнее, чем линейная функция, называется суперполиномиальным.
В идеале, криптограф хотел бы утверждать, что алгоритм, лучший для взлома спроектированного алгоритма шифрования, обладает экспоненциальной временной сложностью. На практике, самые сильные утверждения, которые могут быть сделаны при текущем состоянии теории вычислительной сложности, имеют форму «все известные алгоритмы вскрытия данной криптосистемы обладают суперполиномиальной временной сложностью». То есть, известные нам алгоритмы вскрытия обладают суперполиномиальной временной сложностью, но пока невозможно доказать, что не может быть открыт алгоритм вскрытия с полиномиальной временной сложностью. Развитие теории вычислительной сложности возможно когда-нибудь позволит создать алгоритмы, для которых существование алгоритмов с полиномиальным временем вскрытия может быть исключено с математической точностью.
С ростом n временная сложность алгоритмов может стать настолько огромной, что это повлияет на практическую реализуемость алгоритма.
При условии, что единицей времени для нашего компьютера является микросекунда, компьютер может выполнить постоянный алгоритм за микросекунду, линейный — за секунду, а квадратичный — за 11.6 дня. Выполнение кубического алгоритма потребует 32 тысяч лет, что в принципе реализуемо, компьютер, конструкция которого позволила бы ему противостоять следующему ледниковому периоду, в конце концов получил бы решение. Выполнение экспоненциального алгоритма тщетно, независимо от экстраполяции роста мощи компьютеров, параллельной обработки или контактов с инопланетным суперразумом.
Взглянем на проблему вскрытия алгоритма шифрования грубой силой. Временная сложность такого вскрытия пропорциональна количеству возможных ключей, которое экспоненциально зависит от длины ключа. Если n — длина ключа, то сложность вскрытия грубой силой равна 0(2n). Сложность вскрытия грубой силой при 56-битовом ключе составляет 256, а при 112-битовом ключе — 2112. В первом случае вскрытие возможно, а во втором — нет.
2.1 Сложность проблем
Теория сложности также классифицирует и сложность самих проблем, а не только сложность конкретных алгоритмов решения проблемы. Теория рассматривает минимальное время и объем памяти, необходимые для решения самого трудного варианта проблемы на теоретическом компьютере, известном как машина Тьюринга. Машина Тьюринга представляет собой конечный автомат с бесконечной лентой памяти для чтения записи и является реалистичной моделью вычислений.
Проблемы, которые можно решить с помощью алгоритмов с полиномиальным временем, называются решаемыми, потому что для разумных входных данных обычно могут быть решены за разумное время. (Точное определение «разумности» зависит от конкретных обстоятельств) Проблемы, которые невозможно решить за полиномиальное время, называются нерешаемыми, потому что вычисление их решений быстро становится невозможным. Нерешаемые проблемы иногда называют трудными. Проблемы, которые могут быть решены только с помощью суперполиномиальных алгоритмов, вычислительно нерешаемы, даже при относительно малых значениях n.
Что еще хуже, Алан Тьюринг доказал, что некоторые проблемы принципиально неразрешимы. Даже отвлекаясь от временной сложности алгоритма, невозможно создать алгоритм решения этих проблем.
Задачи можно разбить на классы в соответствии со сложностью их решения. Вот важнейшие из них и предполагаемые соотношения между ними:
P NP (или P=NP). Однако, большинство специалистов, занимающихся теорией сложности, убеждены, что это классы неравны.
Как ни странно, можно доказать, что некоторые NP-задачи настолько же трудны, что и любая задача этого класса. Такие задачи называются NP-полными. То есть, если такая задача решается за полиномиальное время, то P=NP.
Таким образом, для программиста NP-полнота означает полный перебор, причем сложность этого перебора будет экспоненциальной или факториальной. Но следует понимать, что не всякий полный перебор имеет такую сложность. Например, если решать задачи из предыдущего выпуска полным перебором, то сложность полученных алгоритмов будет полиномиальной — O(n2) для задачи про подпоследовательности и O(n6) для задачи про подматрицы.
Наконец, существует класс задач EXPTIME. Эти задачи решаются за экспоненциальное время. В настоящее время можно доказать, что EXPTIME-полные задачи невозможно решить за детерминированное полиномиальное время. Кроме того, доказано, что P<>EXPTIME.
3. Машина Тьюринга и алгоритмически неразрешимые проблемы
За время своего существования человечество придумало множество алгоритмов для решения разнообразных практических и научных проблем. Зададимся вопросом – а существуют ли какие-нибудь проблемы, для которых невозможно придумать алгоритмы их решения?
Утверждение о существовании алгоритмически неразрешимых проблем является весьма сильным – мы констатируем, что мы не только сейчас на знаем соответствующего алгоритма, но мы не можем принципиально никогда его найти.
Успехи математики к концу XIX века привели к формированию мнения, которое выразил Д. Гильберт – «в математике не может быть неразрешимых проблем», в связи с этим формулировка проблем Гильбертом на конгрессе 1900 года в Париже была руководством к действию, констатацией отсутствия решений в данный момент.
Первой фундаментальной теоретической работой, связанной с доказательством алгоритмической неразрешимости, была работа Курта Гёделя – его известная теорема о неполноте символических логик. Это была строго формулированная математическая проблема, для которой не существует решающего ее алгоритма. Усилиями различных исследователей список алгоритмически неразрешимых проблем был значительно расширен. Сегодня принято при доказательстве алгоритмической неразрешимости некоторой задачи сводить ее к ставшей классической задаче – «задаче останова».
Имеет место быть следующая теорема: не существует алгоритма (машины Тьюринга), позволяющего по описанию произвольного алгоритма и его исходных данных (и алгоритм и данные заданы символами на ленте машины Тьюринга) определить, останавливается ли этот алгоритм на этих данных или работает бесконечно.
Таким образом, фундаментально алгоритмическая неразрешимость связана с бесконечностью выполняемых алгоритмом действий, т.е. невозможностью предсказать, что для любых исходных данных решение будет получено за конечное количество шагов.
Тем не менее, можно попытаться сформулировать причины, ведущие к алгоритмической неразрешимости, эти причины достаточно условны, так как все они сводимы к проблеме останова, однако такой подход позволяет более глубоко понять природу алгоритмической неразрешимости:
а) Отсутствие общего метода решения задачи
Проблема 1: Распределение девяток в записи числа;
Определим функцию f(n) = i, где n – количество девяток подряд в десятичной записи числа, а i – номер самой левой девятки из n девяток подряд: =3,141592… f(1) = 5.
Задача состоит в вычислении функции f(n) для произвольно заданного n.
Поскольку число является иррациональным и трансцендентным, то мы не знаем никакой информации о распределении девяток (равно как и любых других цифр) в десятичной записи числа. Вычисление f(n) связано с вычислением последующих цифр в разложении, до тех пор, пока мы не обнаружим n девяток подряд, однако у нас нет общего метода вычисления f(n), поэтому для некоторых n вычисления могут продолжаться бесконечно – мы даже не знаем в принципе (по природе числа) существует ли решение для всех n.
Проблема 2: Вычисление совершенных чисел;
Совершенные числа – это числа, которые равны сумме своих делителей, например: 28 = 1+2+4+7+14.
Определим функцию S(n) = n-ое по счёту совершенное число и поставим задачу вычисления S(n) по произвольно заданному n. Нет общего метода вычисления совершенных чисел, мы даже не знаем, множество совершенных чисел конечно или счетно, поэтому наш алгоритм должен перебирать все числа подряд, проверяя их на совершенность. Отсутствие общего метода решения не позволяет ответить на вопрос о останове алгоритма. Если мы проверили М чисел при поиске n-ого совершенного числа – означает ли это, что его вообще не существует?
Проблема 3: Десятая проблема Гильберта;
Пусть задан многочлен n-ой степени с целыми коэффициентами – P, существует ли алгоритм, который определяет, имеет ли уравнение P=0 решение в целых числах?
Ю.В. Матиясевич показал, что такого алгоритма не существует, т.е. отсутствует общий метод определения целых корней уравнения P=0 по его целочисленным коэффициентам.
б) Информационная неопределенность задачи
Проблема 4: Позиционирование машины Поста на последний помеченный ящик;
Пусть на ленте машины Поста заданы наборы помеченных ящиков (кортежи) произвольной длины с произвольными расстояниями между кортежами и головка находится у самого левого помеченного ящика. Задача состоит установке головки на самый правый помеченный ящик последнего кортежа.
Попытка построения алгоритма, решающего эту задачу приводит к необходимости ответа на вопрос – когда после обнаружения конца кортежа мы сдвинулись вправо по пустым ящикам на М позиций и не обнаружили начало следующего кортежа – больше на ленте кортежей нет или они есть где-то правее? Информационная неопределенность задачи состоит в отсутствии информации либо о количестве кортежей на ленте, либо о максимальном расстоянии между кортежами – при наличии такой информации (при разрешении информационной неопределенности) задача становится алгоритмически разрешимой.
в) Логическая неразрешимость (в смысле теоремы Гёделя о неполноте)
Проблема 5: Проблема «останова» (см. теорема);
Проблема 6: Проблема эквивалентности алгоритмов;
По двум произвольным заданным алгоритмам (например, по двум машинам Тьюринга) определить, будут ли они выдавать одинаковые выходные результаты на любых исходных данных.
Проблема 7: Проблема тотальности;
По произвольному заданному алгоритму определить, будет ли он останавливаться на всех возможных наборах исходных данных. Другая формулировка этой задачи – является ли частичный алгоритм Р всюду определённым?
Заключение
Теория сложности также классифицирует и сложность самих проблем, а не только сложность конкретных алгоритмов решения проблемы. Теория рассматривает минимальное время и объем памяти, необходимые для решения самого трудного варианта проблемы на теоретическом компьютере, известном как машина Тьюринга. Машина Тьюринга представляет собой конечный автомат с бесконечной лентой памяти для чтения записи и является реалистичной моделью вычислений.
Задачи можно разбить на классы в соответствии со сложностью их решения. Вот важнейшие из них и предполагаемые соотношения между ними:
P NP (или P=NP). Однако, большинство специалистов, занимающихся теорией сложности, убеждены, что это классы неравны.
Как ни странно, можно доказать, что некоторые NP-задачи настолько же трудны, что и любая задача этого класса. Такие задачи называются NP-полными. То есть, если такая задача решается за полиномиальное время, то P=NP.
Список литературы
1. Рощин А.Г., Половов Р.М. Теория автоматов. Часть I. Тексты лекций — Москва: МГТУ ГА, 2001. — 76 с.
2. Фалевич Б.Я. Теория алгоритмов. – М.: ИНФРА-М, 2006. – с.324.
3. Фалина Н.М. Машина Тьюринга // Информатика. — №26. – 2005. – с.12-15