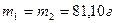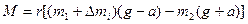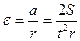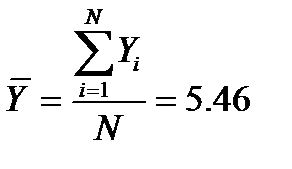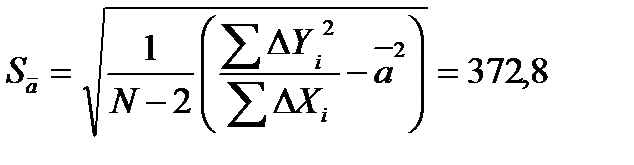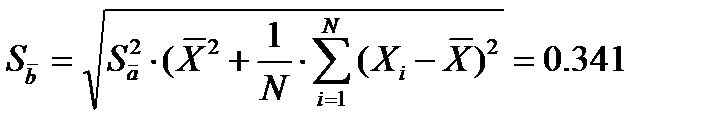Машина Атвуда
Задан вопрос:
В чем заключается проверка основного закона динамики поступательного движения с помощью машины Атвуда?
Можно ли ответить следующим образом?
Когда на концах нити висят грузы одинаковой массы, система находится в положении безразличного равновесия. Если же на один из грузов (обычно на правый) положить перегрузок, то система выйдет из равновесия, и грузы начнут двигаться с ускорением.
Или же ответ другой?

Здравствуйте, формумчане! Решаю задачку по механике и не понимаю кое-каких моментов. Вот.
Думаю, удобство в том что поскольку:
можно подобрать m1 и m2 так, чтобы ускорение было невелико, а влиянием силы трения всё ещё можно было бы пренебречь. Тогда достаточно «секундомера и шнурка от кеда» чтобы, например, измерить пару перемещения и времени из которой найти ускорение:
и убедиться, что это значение удовлетворяет и первой формуле.
Можно решить и обратную задачу определив ускорение свободного падения.
То есть это легче чем найти Пизанскую башню и от-туда чего-нибудь сбросить, замерив высоту и время.
А бросать в лабораторных условиях бессмысленно, так как время слишком мало, учитывая цену деления простых хронометров и скорость реакции человека, если использовать что-то поточнее.
Реферат: Определение момента инерции в машине Атвуда
Определение момента инерции в машине Атвуда
Приборы и принадлежности: машина Атвуда, набор грузов, секундомер, масштабная линейка.
Цель работы: изучение вращательного и поступательного движений на машине Атвуда, определение момента инерции блока и момента сил трения в оси блока.
Описание установки и исследуемые закономерности

На среднем кронштейне 4 крепится фотодатчик 8, выдающий электрический сигнал по окончанию счета времени равноускоренного движения грузов. На среднем кронштейне есть риска, совпадающая с оптической осью фотодатчика. Нижний кронштейн представляет собой площадку с резиновым амортизатором, о который ударяется груз при остановке. На вертикальной стойке 1 укреплена миллиметровая линейка 9, по которой определяют начальное и конечное положение грузов, т.е. пройденный путь.
Начальное положение определяют визуально по нижнему краю груза, конечное положение – по риске среднего кронштейна. Секундомер 10 выполнен как самостоятельный прибор с цифровой индикацией времени.
Машина Атвуда предназначена для изучения законов поступательного и вращательного движений. Принцип работы установки основан на том, что, когда на концах нити подвешены грузы различной массы, система начинает двигаться равноускоренно. В комплект грузов входит несколько перегрузов, что позволяет исследовать движения с различными ускорениями.
На каждый груз действует две силы – сила тяжести и сила натяжения нити, под действием которых грузы движутся. Полагая, что нить невесома и нерастяжима, получим, что ускорения обоих грузов будут постоянны, одинаковы по значению и противоположны по направлению.
На основании второго закона Ньютона для первого груза с перегрузом и второго груза можно записать
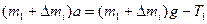
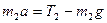
где m1 и m2 – массы 1-го и 2-го грузов; 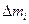
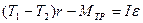
где r – радиус блока; 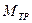
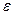
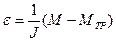
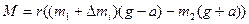
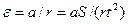
где S– пройденный грузом за время tпуть.
Целью выполнения работы является определение момента инерции блока и момента сил трения в блоке. Для этого экспериментально исследуется зависимость М от ε. Различные значения М реализуются с помощью набора перегрузов массой 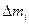
| Название: Определение момента инерции в машине Атвуда Раздел: Рефераты по физике Тип: реферат Добавлен 23:52:38 23 июня 2011 Похожие работы Просмотров: 110 Комментариев: 19 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать |
| t, c | |
| Перегруз 1,3 г | |
| 1 | 2,61 |
| 2 | 2,761 |
| 3 | 2,77 |
| Перегруз 2,2 г | |
| 1 | 2,226 |
| 2 | 2,242 |
| 3 | 2,229 |
| Перегруз 2,6 г | |
| 1 | 1,95 |
| 2 | 1,968 |
| 3 | 1,937 |
| Перегруз 3,9 г | |
| 1 | 1,597 |
| 2 | 1,525 |
| 3 | 1,54 |
| Перегруз 4,8 г | |
| 1 | 1,445 |
| 2 | 1,444 |
| 3 | 1,467 |
| Перегруз 5,8 г | |
| 1 | 1,285 |
| 2 | 1,299 |
| 3 | 1,283 |
Значение масс
Значение с прибора 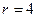
Для определения I и 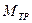
—
—
Для каждого случая.
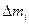
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ В МАШИНЕ АТВУДА



ОТЧЕТ
по лабораторно-практической работе № 5
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
В МАШИНЕ АТВУДА
Выполнил Гладких Н.А.
Преподаватель Морозов В.В
| Оценка лабораторно-практического занятия | |||||
| Выполнение ИДЗ | Вопросы | Подготовка к лабораторной работе | Отчет по лабораторной работе | Коллоквиум | Комплексная оценка |
“Выполнено” “____” ___________Подпись преподавателя __________
ЛАБОРАТОРНАЯ РАБОТА № 5
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ В МАШИНЕ АТВУДА
Цель работы: изучение вращательного и поступательного движений на машине Атвуда, определение момента инерции блока и момента сил трения в оси блока.
Описание установки и её назначение.
Машина Атвуда является настольным прибором, ее изображение приведено на рис. 3.1. На вертикальной стойке 1 основания 2 расположены три кронштейна: нижний 3, средний 4 и верхний 5. На верхнем кронштейне 5 крепится блок с узлом подшипников качения, через который переброшена нить с грузом 6. На верхнем кронштейне находится электромагнит 7, который при подаче на него напряжения с помощью фрикциона удерживает систему с грузами в неподвижном состоянии.
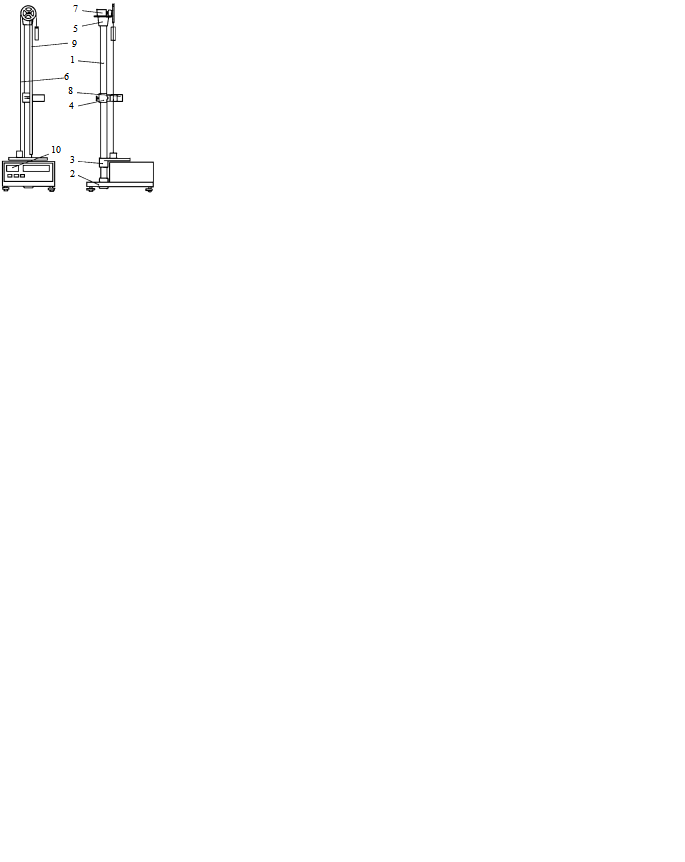 Рис. 3.1 Рис. 3.1 |
На среднем кронштейне 4 крепится фотодатчик 8, выдающий электрический сигнал по окончании счета времени равноускоренного движения грузов. Также на вертикальной стойке 1 укреплена миллиметровая линейка 9, по которой определяют начальное и конечное положения грузов, т. е. пройденный путь.
Начальное положение определяют визуально по нижнему краю груза, конечное положение – по риске среднего кронштейна. Секундомер 10 выполнен как самостоятельный прибор с цифровой индикацией времени.
Машина Атвуда предназначена для изучения законов поступательного и вращательного движений. Принцип работы установки основан на том, что, когда на концах нити подвешены грузы различной массы, система начинает двигаться равноускоренно. В комплект грузов входит несколько перегрузов, что позволяет исследовать движения с различными ускорениями.
Основные расчетные формулы.
2. M = r ((m1 + Dmi) (g – a) – m2(g + a)) – развернутая формула 1. Где m1и m2– массы 1-го и 2-го грузов; Dmi– масса перегруза, находящегося на 1-м грузе; a – ускорение грузов.
e = a / r = 2 S / (r t2) – формула для определения углового ускорения блока.
| № | t, сек | 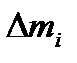 , кг , кг | M, 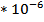 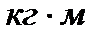 | 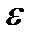 , , 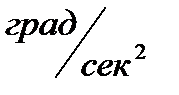 | a, 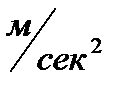 |
| Для перегруза №1 | |||||
| 2.265 | 0.0013 | 2.853 | 0.117 | ||
| 2.426 | 0.0013 | 2.486 | 0.102 | ||
| 2.337 | 0.0013 | 2.679 | 0.11 | ||
| Для перегруза №2 | |||||
| 1.884 | 0.0022 | 4.123 | 0.169 | ||
| 1.791 | 0.0022 | 4.562 | 0.187 | ||
| 1.849 | 0.0022 | 4.28 | 0.176 | ||
| Для перегрузов №3 | |||||
| 1.635 | 0.0026 | 5.474 | 0.224 | ||
| 1.741 | 0.0026 | 4.828 | 0.198 | ||
| 1.780 | 0.0026 | 4.619 | 0.189 | ||
| Для перегрузов №4 | |||||
| 1.400 | 0.0032 | 7.466 | 0.306 | ||
| 1.438 | 0.0032 | 7.077 | 0.29 | ||
| 1.390 | 0.0032 | 7.574 | 0.311 | ||
| Для перегрузов №1+№3 | |||||
| 1.325 | 0.0039 | 8.336 | 0.342 | ||
| 1.344 | 0.0039 | 8.102 | 0.332 | ||
| 1.330 | 0.0039 | 8.273 | 0.339 | ||
| Для перегрузов №2+№3 | |||||
| 1.117 | 0.0048 | 11.729 | 0.481 | ||
| 1.124 | 0.0048 | 11.583 | 0.475 | ||
| 1.132 | 0.0048 | 11.42 | 0.468 | ||
| Для перегрузов №3+№4 | |||||
| 1.028 | 0.0058 | 13.848 | 0.568 | ||
| 1.055 | 0.0058 | 13.148 | 0.539 | ||
| 1.050 | 0.0058 | 13.274 | 0.544 |
Из сопоставлений линейной зависимости 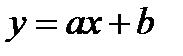
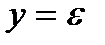
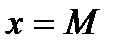
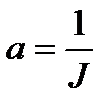
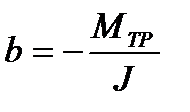
Заменив в этих формулах XK на МК, а YK на 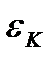
Среднее значение X(MK), Y( 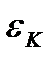

Вычисляем среднее значение коэффициентов а и b:
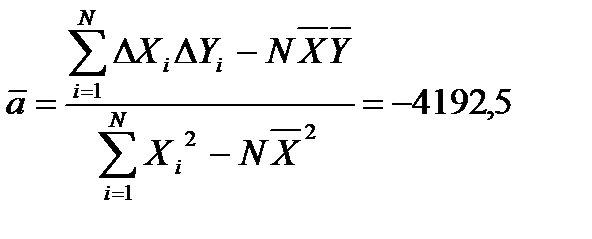
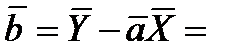
Вычисляем средние квадратические отклонения для средних 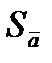
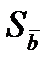
Вычисляем доверительную погрешность 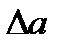
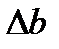
При каком условии можно пренебречь моментом инерции блока машины атвуда не допуская большой ошибки
Лабораторная работа № КСЕ-02
Изучение ДИНАМИЧЕСКИХ ЗАКОНОМЕРНОСТЕЙ
на механической модели – МАШИНЕ АТВУДА
Цель работы:
1. Ознакомиться с динамическими закономерностями на примере законов кинематики и динамики материальной точки.
2. Проверить закон равноускоренного движения тела.
3. Проверить второй закон Ньютона для тела постоянной массы.
Теоретическое введение
Закономерности, описывающие природные процессы и явления, подразделяются на динамические и статистические.
Динамические закономерности позволяют, зная состояние объекта в некоторый момент времени, однозначно и сколь угодно точно определить его состояние в любой предшествующий или последующий момент времени. Пример динамических закономерностей – законы классической механики. Область применения динамических закономерностей – сравнительно простые, например механические, системы. Динамические закономерности не учитывают фактор случайности.
Более общий характер имеют статистические (вероятностные) закономерности, учитывающие влияние фактора случайности на исследуемые объекты и процессы. Они определяют поведение сложных (состоящих из большого числа элементов) систем и микроскопических – квантовых – систем. Динамические закономерности – частный случай статистических. Статистические закономерности переходят в динамические, если ролью случайностей можно пренебречь.
В данной работе мы знакомимся с динамическими закономерностями на примере законов механики, описывающих движение материальной точки.
В механике возникает общий для всего естествознания вопрос об описании состояния исследуемого объекта. Описать состояние объекта в данный момент времени означает дать минимальный набор информации о нем, на основании которого, располагая также информацией о внешних воздействиях на объект, можно предсказать его состояние в любой последующий момент времени, то есть предсказать его движение (развитие).
Познакомимся с описанием состояния объекта и динамическими закономерностями на примере материальной точки, могущей совершать одномерное механическое движение, то есть перемещаться в пространстве лишь вдоль одной оси – оси ОХ. Ограничимся случаем движения со скоростью, много меньшей скорости света, который изучает так называемая классическая (ньютоновская) механика.
При изучении движения тел нужно выбрать некоторую систему отсчета, включающую в себя тело отсчета, связанную с ним систему координат и часы. Положение материальной точки относительно выбранной системы координат можно описать различными способами. Простейший из них – координатный. При одномерном движении относительно оси ОХ положение точки в каждый момент времени характеризует ее координата х (при двух- и трехмерном движении – две и три координаты, соответственно). Говорят, что известен закон движения точки, если известно, как ее положение относительно выбранной системы координат зависит от времени. Закон одномерного движения материальной точки может быть задан аналитически в виде зависимости координаты точки от времени x(t).
Важнейшими кинематическими характеристиками движения точки являются ее скорость и ускорение. Скорость характеризует быстроту движения точки. Быстроту одномерного движения точки вдоль оси ОХ характеризует проекция мгновенной скорости точки на эту ось (далее для краткости слово «мгновенная» опущено). По определению – это предел, к которому стремится отношение приращения (изменения) координаты точки Δх к соответствующему промежутку времени Δt, при условии, что Δt стремится к нулю. Иначе говоря, это – первая производная от координаты точки по времени:
Ускорение характеризует быстроту изменения скорости. При одномерном движении используется проекция ускорения на ось ОХ, обозначаемая ах и равная пределу, к которому стремится отношение приращения проекции скорости точки к соответствующему промежутку времени Δt, при условии, что Δt стремится к нулю. Иначе говоря, это – первая производная от проекции скорости точки по времени или вторая производная от координаты точки по времени:
Динамика базируется на трех законах Ньютона.
Первый закон Ньютона (закон инерции) утверждает, что существует система отсчета (так называемая инерциальная система отсчета), относительно которой свободная материальная точка (точка, на которую не действуют внешние силы) сохраняет состояния покоя или прямолинейного равномерного движения, пока воздействие со стороны других тел не выведет точку из этого состояния. Равномерное прямолинейное движение свободной точки называют движением по инерции, а способность тела сохранять состояние покоя или равномерного прямолинейного движения – инертностью тела. Инерциальные системы отсчета важны тем, что только в них выполняются второй и третий законы Ньютона. Понятие инерциальной системы отсчета является абстракцией, так как ни одна из реально используемых систем отсчета не является, строго говоря, инерциальной. Однако при решении многих практических задач можно считать инерциальной систему отсчета, связанную с Землей.
Второй закон Ньютона устанавливает связь между изменением состояния движения точки и внешним силовым воздействием на нее. Второй закон Ньютона в общем виде гласит: скорость изменения импульса материальной точки равна действующей на эту точку силе:
Если масса точки постоянна, то второй закон Ньютона принимает вид:
Второй закон Ньютона, записанный в виде (2.5), называют дифференциальным уравнением движения материальной точки вдоль оси ОХ.
В динамике рассматриваются две основные задачи. При решении прямой задачи задаются масса точки и закон ее движения, в одномерном случае – зависимость x(t). Требуется найти зависимости от времени кинематических характеристик: скорости и ускорения, а также силы, действующей на тело при данном движении. Задача решается однозначно: путем дифференцирования закона движения находятся скорость и ускорение (формулы (2.1) и (2.2)), по второму закону Ньютона находится сила.
Второй закон Ньютона для точки постоянной массы (2.4) и получающийся из него закон равноускоренного одномерного движения (2.8) – примеры динамических закономерностей из области механики. В данной работе осуществляется проверка этих двух законов.
Описание установки и метода измерения
Машина Атвуда (рисунок 2.1) изобретена в 1784 г. и предназначена для изучения законов поступательного движения тел под действием постоянной силы. Установка представляет собой блок 1, через который перекинута нить. На концах нити закреплены основные грузы равной массы М, на которые можно помещать дополнительные грузы (перегрузки), масса каждого из которых равна m. В исходном состоянии левый груз удерживается электромагнитом 2 в крайнем нижнем положении.
Пусть на правый основной груз помещено N1, а на левый N2 дополнительных грузов, причем N1>N2. Общая масса m1=(М + N1m) правого набора грузов (основного и дополнительных) превышает общую массу m2=(М +N2m) левого набора грузов, вследствие этого после отключения электромагнита система приходит в движение и начинается отсчет времени движения.
Установка снабжена линейкой для измерения пути, который проходит правый груз, и автоматической системой отсчета времени движения 3. При достижении правым грузом финишной платформы 4 отсчет времени движения прекращается.
Покажем, что при этом движение системы грузов будет равноускоренным. Пренебрежем массой блока. Запишем формулу второго закона Ньютона для каждого из тел системы:
Запишем проекции этих векторных равенств на ось ОХ. При этом учтем, что блок и нить невесомы, следовательно, Т1 = Т2 = Т. Кроме того, нить нерастяжима, следовательно, а1 = а2 = а.
С учетом этого получаем:
Вычтем из первого уравнения второе:
Из формул (2.11), (2.12) следует, что при фиксированных значениях величин N1 и N2 результирующая сила Fp и ускорение системы грузов постоянны.
Таким образом, данная установка позволяет, во-первых, проверить справедливость закона равноускоренного движения (2.8). В эксперименте начальная координата правого груза и начальная скорость грузов равны нулю, а конечная координата правого груза равна пройденному пути S. При этих условиях закон движения (2.8) принимает вид:
Задавая путь и измеряя время движения, можно экспериментально проверить справедливость закона (2.13).
Во-вторых, перекладывая перегрузки с правого основного груза на левый, можно, не изменяя массы системы, изменять результирующую силу. Это позволяет изучить влияние силы на ускорение системы постоянной массы, то есть проверить справедливость второго закона Ньютона для тела постоянной массы.
Часть 1. Проверка закона равноускоренного движения
Порядок выполнения работы
1. Подключить установку к сети, включить секундомер, нажать кнопку «СБРОС» («установка нуля»).
2. Установить на правом основном грузе несколько перегрузков общей массой N1m = 5-7 г, записать значение N1m в таблицу 2.1. Левый груз установить на электромагнит.
3. Установить финишную платформу на некоторое расстояние S (примерно 20 см), используя винтовой фиксатор. Записать значение S в таблицу 2.1.
ВНИМАНИЕ! Перед нажатием кнопки «ПУСК» необходимо убедиться, что грузы не совершают колебательных и вращательных движений.