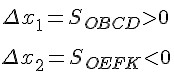Постройте график зависимости модуля скорости автомобиля от времени, если он из состояния покоя движется равноускоренно и прямолинейно и через 10 с с его скорость становится равной 40 м / с?
Постройте график зависимости модуля скорости автомобиля от времени, если он из состояния покоя движется равноускоренно и прямолинейно и через 10 с с его скорость становится равной 40 м / с.
Автомобиль движется прямолинейно вдоль оси ×.
Уравнение зависимости проекции вектора скорости автомобиля от времени в СИ выглядит так : U× = 10 + 0, 5t.
Определите модуль и направление начальной скорости и ускорения автомобиля.
Как меняется модуль вектора скорости автомобиля?
Как направлена равнодействующая сил, приложенных к автомобилю(см?
Как направлена равнодействующая сил, приложенных к автомобилю(см.
Рисунок), если он движется равноускоренно прямолинейно с уменьшающейся по модулю скоростью?
Постройте график зависимости модуля скорости от времени для автомобиля, который движется прямолинейно равноускоренно, если начальная скорость равна 10 м / c, а ускорение 2 м / с2?
Постройте график зависимости модуля скорости от времени для автомобиля, который движется прямолинейно равноускоренно, если начальная скорость равна 10 м / c, а ускорение 2 м / с2.
По графику зависимости модуля скорости от времени определите ускорение прямолинейно движущегося тела в момент времени 2 с?
По графику зависимости модуля скорости от времени определите ускорение прямолинейно движущегося тела в момент времени 2 с.
Помогите плизззззззззззПостройте график зависимости модуля скорости от времени для автомобиля движущегося прямолинейно равноускоренно с начальной скоростью 10м / си укорением 2м / с2?
Постройте график зависимости модуля скорости от времени для автомобиля движущегося прямолинейно равноускоренно с начальной скоростью 10м / си укорением 2м / с2.
Направления ускорения и начальной скорости одинаковы.
По графику зависимости модуля скорости от времени определите ускорение прямолинейно движущегося тела в момент времени t = 2 с?
По графику зависимости модуля скорости от времени определите ускорение прямолинейно движущегося тела в момент времени t = 2 с.
Поезд движется равномерно и прямолинейно, со скростью 72 км / ч?
Поезд движется равномерно и прямолинейно, со скростью 72 км / ч.
Постройте графики зависимости :
1)перемещения от времени
2)скорости от времени
Автомобиль двигаясь прямолинейно и равномерно за 2 часа прошел 120 км.
Постройте график зависимости.
1)перемещения от времени
2)скорости от времени.
Самолет разгоняется из состояния покоя прямолинейно с ускорением 1, 5 м \ с в течение 40 секунд?
Самолет разгоняется из состояния покоя прямолинейно с ускорением 1, 5 м \ с в течение 40 секунд.
Определите скорость самолета в конце разгона.
Постройте график зависимости скорости движения самолета от времени.
Тело движется равноускоренно с ускорением 5 М / С ^ 2 из состояния покоя?
Тело движется равноускоренно с ускорением 5 М / С ^ 2 из состояния покоя.
Через сколько времени его скорость будет равна 80М / С.
На рисунке 1?
50 показан график зависимости проекции скорости тела от времени.
Постройте график зависимости модуля перемещения от времени.
Чем больше витков в катушке, тем сила тока больше. Также увеличить силу тока можно с помощью сердечника.
F = pgV если мы поместим брусок в воду то p = 1000 V = 0, 02 × 0, 05 × 0, 1 = 0, 0001 м ^ 3 F = 1000 × 10 × 0, 0001 = 1 Н Ответ : 1 Н.
График зависимости модуля скорости от времени
при прямолинейном равноускоренном движении график зависимости модуля скорости от времени — отрезок прямой.
Чтобы построить такой график, достаточно найти две принадлежащие ему точки и провести через них отрезок прямой.
Рассмотрим на примерах, как построить график зависимости модуля скорости от времени и какую информацию о движении тела можно получить, изучая такой график.
1. Построим график зависимости от времени модуля скорости свободно падающего тела, если: а) начальная скорость тела равна нулю; б) начальная скорость тела направлена вниз и 
Решение. Найдем по две точки для каждого графика — соответствующую начальному моменту времени и соответствующую моменту времени t = 1с.
В случае а) зависимость модуля скорости от времени выражается формулой υ = gt, поэтому при t = 0 с скорость тела равна нулю, а при t = 1с скорость тела равна 
(Соответствующие точки графика обозначены красным на рис. 3.4.)
В случае б) зависимость модуля скорости от времени выражается формулой υ = υ0 + gt, где 
Поэтому при t = 0 с скорость тела равна 
а при t = 1с скорость тела 
ответствующие точки графика обозначены зеленым на рис. 3.4.)
Рис. 3.4. Графики зависимости модуля скорости от времени для прямолинейного равноускоренного движения: а — без начальной скорости; б — с начальной скоростью
Проводя через найденные точки отрезки прямых, получаем искомые графики (см. рис. 3.4).
Построенные графики оказались параллельными отрезками. Обусловлено это тем, что тела́ двигались с одинаковым ускорением.
Постройте график зависимости модуля скорости автомобиля
§ 15. Графики зависимости модуля и проекции скорости равномерного прямолинейного движения от времени
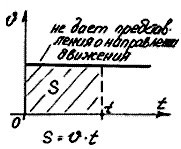
1. График модуля скорости.
Зная график модуля скорости, можно найти не только модуль скорости, но и путь S, пройденный точкой. Он численно равен площади прямоугольника, расположенного под графиком модуля скорости.
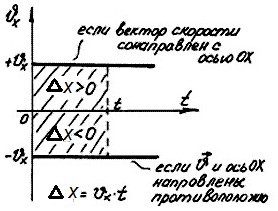
2. Графики проекции скорости.
Так как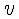 
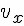
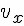
= const, то и 
= const. Поэтому графиками также будут прямые линии, параллельные оси времени. Но в отличие от модуля проекции могут быть как положительными, так и отрицательными. Поэтому графиком = f (t) является прямая, параллельная оси времени, которая может быть расположена как выше, так и ниже оси t.
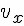
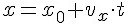
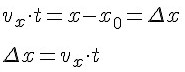
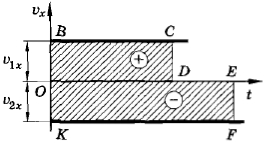
По графикам можно найти проекцию и модуль скорости. По знаку проекции скорости можно судить о направлении движения точки относительно оси OX. Если > 0, то вектор скорости точки сонаправлен с осью OX, и точка движется в положительном направлении оси. Если же
.
.
Изменение координаты движущейся точки численно равно площади прямоугольника между графиком проекции скорости и осью времени. Площади приписывают знак «плюс» или «минус». Если график расположен выше оси времени, то площадь считают положительной, и изменение координаты движущейся точки больше нуля. Если график расположен ниже оси времени, то площадь считают отрицательной, и изменение координаты движущейся точки меньше нуля.
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
Графики прямолинейного движения
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: \(\vec =0\).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: \(\vec =const\). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
Для каждого вида движения получим три графика. Графики будем называть так:
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой \(x_<0>\) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
\[x=x_<0>\]
Скорость и ускорение неподвижного тела равны нулю:
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка \(x_<0>\), а конечная координата — точка \(x\) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
Ускорение есть (рис. 4г) и оно не меняется:
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов \(\vec
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
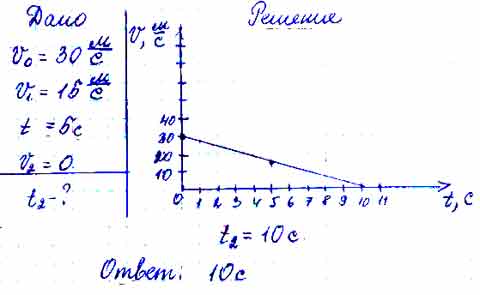
По условию задачи 3.10 постройте график зависимости модуля скорости автомобиля от времени. По графику определите, через сколько секунд посл.
В 6:02 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: По условию задачи 3.10 постройте график зависимости модуля скорости автомобиля от времени. По графику определите, через сколько секунд после начала торможения автомобиль остановится.
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
ответ к заданию по физике 
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.