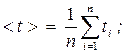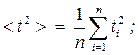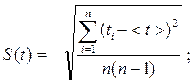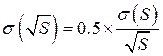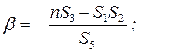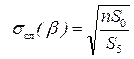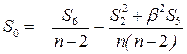Изучение законов падения на машине атвуда лабораторная работа

Лабораторная работа: Изучения прямолинейного движения на машине атвуда

Федеральное Агентство по образованию

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Лабораторная работа по курсу «Общая физика»

ИЗУЧЕНИЕ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ ТЕЛ

Преподаватель Студент группы 220201

___________ /____________. / Стороженко Сергей Валерьевич

___________2011 г. 2011 г.

Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.

2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА

Название: Изучения прямолинейного движения на машине атвуда Раздел: Рефераты по физике Тип: лабораторная работа Добавлен 12:55:38 22 июня 2011 Похожие работы Просмотров: 3892 Комментариев: 18 Оценило: 5 человек Средний балл: 4.8 Оценка: неизвестно Скачать

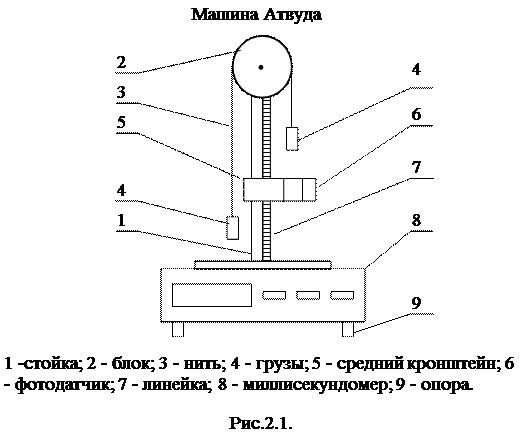Схема экспериментальной установки на основе машины Атвуда приведена на рис.2.1.

Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе.

Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться.

3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ

Средние значения времени и квадрата времени 2 > прохождения грузом с перегрузом пути S:

Абсолютная суммарная погрешность измерения времени прохождения пути S:

(3.3)

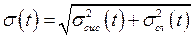
Абсолютная случайная погрешность измерения времени прохождения пути S:

стандартная абсолютная погрешность измерения времени:

Абсолютная суммарная погрешность косвенного измерения квадрата времени прохождения пути S:

Абсолютная погрешность косвенного измерения корня квадратного из расстояния:

Угловой коэффициент экспериментальной прямой:

b =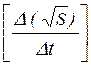 (3.8)

Величина ускорения, определяемого из линеаризованного графика:

Абсолютную случайную погрешность ускорения s_сл (a ) рассчитываем методом наименьших квадратов.

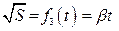
Рассчитываем параметры линеаризованного графика

(y = f(x) = Ax + B) и случайные абсолютные погрешности параметров.

Расчет производится по формулам: (3.10)

куда входят следующие величины:

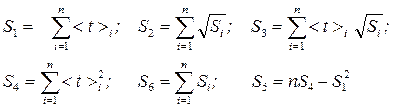
где n – число экспериментальных точек.

Абсолютная случайная погрешность определения углового коэффициента: s_сл (β ):

где вспомогательная величина:

Абсолютная случайная погрешность ускорения:

4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.

Измеренные значения и результаты их обработки приведены в таблице 4.1.

Результаты прямых и косвенных измерений Таблица 4.1

=3,16 см 1/2

= 4,47 см 1/2

= 5,48 см 1/2

= 5,92 см 1/2

=6,48 см 1/2

Источник

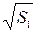
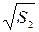
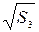
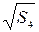
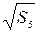
Методические указания к лабораторной работе «Машина Атвуда»

Экспериментальная проверка основных уравнений и законов поступательного движения тела в поле сил земного тяготения, определение ускорения свободного падения лабораторной установке – машине Атвуда.

Время движения грузов измеряется с помощью ручного или стационарного секундомера.

Для выполнения работы машина Атвуда должна быть установлена строго вертикально, что легко проверить по параллельности шкалы и нити.

Второй закон Ньютона в проекциях на вертикальную ось для каждого из тел системы (рис.2) в предположении невесомости блока, отсутствия силы трения и нерастяжимости нити дает:

(1)

(2)

Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то

(3)

Третье соотношение часто называют законом перемещений: «Перемещение при равноускоренном движении прямо пропорционально квадрату времени движения».

Соотношение (3) может быть проверено экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение, с которым движется тело, прямо пропорционально равнодействующей действующих на него сил и обратно пропорционально массе этого тела».

Подставляя a _i в (2) получаем следующую формулу:

(4)

(5)

— сумма проекций на ось Z всех сил, действующих на вращающиеся тело; α- угловое ускорение блока; J – его момент инерции

(6)

Выразим из уравнения (1) разность сил натяжения ( T ₁ – T ₂ ) и подставив ее в уравнение (6) получим:

(7)

Выразим ускорение грузов a :

(8)

Учитывая, что значение момента инерции блока

(9),

k- коэффициент распределения массы блока относительно оси вращения (k

11)

Задание 1. Проверка второго закона Ньютона.

Поскольку ускорение движения является функцией двух переменных – силы и массы, то изучение второго закона Ньютона выполняется путем раздельного исследования двух зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе системы и 2) зависимости ускорения от массы системы при постоянной действующей силе.

Исследование зависимости ускорения от силы при постоянной массе

Измерения и обработка результатов

3. Измеряют время равноускоренного движения системы на пути, например, 1 метр. Все данные заносят в таблицу 1.3 отчета.

4. Пользуясь законом путей (1.6), вычисляют ускорение а.

5. Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.

6. Строят график зависимости ускорения движения от действующей силы. Точку ( F =0, a =0) на графике не откладывают. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод о том, что ускорение действительно прямо пропорционально силе.

7. По угловому коэффициенту полученной прямой определяют массу системы и сравнивают ее реальной массой.

Исследование зависимости ускорения от массы при постоянной силе

Измерения и обработка результатов

1. Все опыты проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе. Ускорение системы измеряется также как и в предыдущем задании.

2. Для изменения массы системы одновременно на правый и левый груз кладут дополнительные одинаковые грузы. Все данные записывают в таблицу отчета.

3. График обратно пропорциональной зависимости ускорения от массы представляет собой гиперболу, которую невозможно идентифицировать. Для проверки предположения об обратно пропорциональной зависимости между ускорением и массой необходимо построить график зависимости ускорения от обратного значения массы системы: a = f (М -1 ). Подтверждением предположения является прямолинейность этого графика.

4. По угловому коэффициенту полученной прямой определяют значение приложенной силы и сравнивают ее с реально действующей в системе

Задание 2. Определение ускорения движения грузов

В полученном уравнении прямой коэффициент k равен половине ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов ( a =2 k ) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет.

Задание 3. Определение ускорения свободного падения

(Выполняется по результатам измерений и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и перегрузка, а также ускорение движения системы, из формулы (3) найдите ускорение свободного падения. Результаты занесите в отчет. В выводе сравните полученный результат с табличной величиной.

Для нахождения погрешности измерения величины ускорения свободного падения Δ g используем формулу:

12)

где ; ; ; ;

– частные производные функции

Проанализируйте результаты своих наблюдений и сформулируйте вывод.

Контрольные вопросы

Какое движение называется поступательным?

Дайте определение инерциальной системы отсчета. Приведите примеры ИСО.

Сформулируйте первый закон Ньютона. Приведите примеры его проявления.

Дайте определение инертной массы тела. Гравитационной? От чего и как зависит масса тела?

Сформулируйте второй закон Ньютона. Приведите варианты его математической формы.

Покажите все силы, действующие на один из грузов в машине Атвуда, и составьте для него уравнение динамики.

Запишите систему уравнений динамики для машины Атвуда с учетом момента инерции блока. Силы трения в блоке?

Источник

лаб 1. Лабораторная работа 1. Исследование прямолинейного движения тел на машине Атвуда цель работы

Дисциплина: Фундаментальное естествознание. Физика.
Преподаватель: Марценюк Н.О

Лабораторная работа №1.

«Исследование прямолинейного движения тел на машине Атвуда»

Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.

Порядок выполнения работы

Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ

1.Измеряем расстояние L с помощью линейки и занесём результат в таблицу измерений 1. Цена деления линейки 1 см.

Таблица 1

m =0,013 кг			L=0,33 м	L2=0,25 м
№ наблюдения	Время ti , с
1	0,549
2	0,565
3	0,548
4	0,554
5	0,571

Таблица 2

Отклонение от каждого из пяти измерений :

Возводим в квадрат каждое отклонение:

Сумма квадратов отклонений:

(t_i— ) 2 =0,0001+0,0001+0,0001+0.0000+0,0002=0,0005с 2
3.Рассчитаем среднее квадратичное отклонение , применив для его расчёта формулу для выборочной оценки S( ) стандартного отклонения результата измерения по формуле из теории погрешностей

S( ) = =0,005 с

4 Умножив это значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени

где t_P()  коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы =n-1.

Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается.

Тогда результат измерения времени t запишем в виде

t=0,56 м/с 2 ± 0,05м/с 2
5.Производим расчет относительной погрешности в определении времени E_t (в процентах) по формуле:

E_t=0,05/0,56*100%=8.44%
Приборная погрешность в определении расстояний уже не может быть отброшена, так как случайной погрешности здесь нет, Тогда для расстояний L и L₂ имеем приборные погрешности, равные половине цены деления линейки

Среднее ускорение грузов рассчитывается по формуле, в которую подставляется среднее значение времени и измеренные линейкой значения расстояний L и L₂.

= 0,25 2 / 2*0,557 2 (0,33-0,25) = 0,0625/0.025=1,26=1,3 м/с 2

Относительная погрешность в определении ускорения а найдётся по формуле:

Абсолютная погрешность находится согласно формуле: Δa = ε_a·
ε_a= = =0,215 = 0,2 м/с2
Δa=0,2*0,7=0,14м/с2

6. Результат измерения ускорения а запишется в виде

a = ± Δa= 0,7 м/с 2 ± 0,2 м/с 2
ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

7. Определяем среднюю величину ускорения свободного падения g по формуле

= =13,3=м/с 2
При этом значение массы грузов принять равным M=90 г.=0,09кг

8. Полуширину доверительного интервала g находим с помощью формулы

Значения погрешностей в определении масс в данной работе принять равными приборной погрешности при их взвешивании:

∆g/g= = = 0,07009= 0,07 м/с 2
9. Рассчитаем абсолютную погрешность ускорения свободного падения Δg аналогично погрешности ускорения a. Представляем результат в стандартной форме g = ± Δg
g = 13,3 ± 0,07 м/с 2

Источник

МУ 4586: Изучение динамики поступательного движения тела с помощью машины Атвуда

Лабораторная работа 1-16: Изучение динамики поступательного движения тела с помощью машины Атвуда

Цель работы: изучение динамики поступательного движения тела в поле сил земного тяготения, определение ускорения свободного паде- ния.

Приборы и принадлежности: машина Атвуда, блок электронный ФМ-1/1, набор грузов и перегрузков.

Элементы теории и метод эксперимента

Машина Атвуда используется для изучения законов динамики движения тел в поле земного тяготения. Она представляет собой на- стольный прибор, изображенный на рис. 1.

Принцип работы машины Атвуда заключается в следующем. Если на концах нити висят грузы A и B одинаковой массы M, то система должна находиться в положении безразличного равновесия. Когда на один из грузов (например, груз B) кладут перегрузок С массы m, то система выходит из положения равновесия и грузы А и B начинают двигаться равноускоренно. В комплект установки, помимо грузов, входит несколько перегрузков различной массы, что позволяет изучать движение с различными ускорениями.

Согласно второму закону Ньютона

где a – ускорение груза вместе с перегрузком.

На левый груз будут действовать две силы: Mg и

Так как блок невесом, то равен

Измеряя пройденный правым грузом путь S и время движения t, можно проверить равноускоренный характер движения груза:

Определение ускорения свободного падения, казалось бы, можно провести на основе формулы (4). Пусть а_э — экспериментальное ускоре- ние, вычисленное из (5). Подставляя а_э в (4), получаем

Однако вычисление g по формуле (6) и сопоставление его с таб- личным покажут, что вычисленное и табличное значения g плохо согла- суются друг с другом. Такое расхождение связано со следующими при- чинами.

Попробуем учесть теоретически, как эти величины видоизменяют соответствующие формулы для вычисления величин а и g, и опишем методику обработки полученных результатов в каждом опыте.

Для этого рассмотрим вращательное движение блока машины Атвуда. Основной закон динамики вращательного движения тела имеет вид

Сумма Mzi — сумма проекций на ось z всех моментов сил, действующих на вращающееся тело; e — его угловое ускорение; J — момент инерции тела.

Направим ось z вдоль оси вращения блока. При движении грузов

на блок действуют вращающий момент (T1 — T2 )r и момент силы трения –M_тр. Тогда уравнение (7) примет вид

где g_э — экспериментальное значение ускорения свободного падения.

Формула (16) может служить основой для экспериментального оп- ределения ускорения свободного падения.

Подготовка установки к работе

Порядок выполнения работы

Для каждого из перегрузков m_i, входящих в комплект лаборатор- ной установки, проведите серии опытов в указанном порядке.

8. Повторите пп. 3 – 7 ещё два раза.

9. Повторите пп. 1 – 8 ещё два раза для различных значений пути S.

Задание 1. Проверка равноускоренного характера движения перегрузков

Для каждого перегрузка m_iпостройте график зависимости S от

Ошибки измерений часто приводят к тому, что экспериментальные точки данной зависимости не лежат на одной прямой. Поэтому через точки следует провести «наилучшую прямую», т. е. прямую, проходящую на наименьшем расстоянии от большинства точек.

Задание 2. Определение ускорения свободного падения

Вопросы и задания для самоконтроля

Библиографический список

Изучение динамики поступательного движения тела с помощью машины Атвуда / Рязан. гос. радиотехн. ун-т; cост.: М.А. Буробин. Рязань, 2012. 8 с.

Содержат основные теоретические сведения, порядок выполнения работы и итоговые контрольные вопросы.

Предназначены для студентов всех направлений подготовки бакалавров и специальностей, изучающих дисциплину «Физика».

Табл. 1. Ил. 2. Библиогр.: 3 назв.

Машина Атвуда, ускорение, равноускоренное движение, ускорение свободного падения

Печатается по решению редакционно-издательского совета Рязанского государственного радиотехнического университета.

Рецензент: кафедра общей и экспериментальной физики РГРТУ (зав. кафедрой доц. М.В. Дубков)

Изучение динамики поступательного движения тела с помощью машины Атвуда

Составитель: Б у р о б и н Михаил Анатольевич

Редактор Р.К. Мангутова Корректор С.В. Макушина

Подписано в печать 20.04.12. Формат бумаги 60 × 84 1/16.

Бумага газетная. Печать трафаретная. Усл. печ. л. 0,5.

Тираж 200 экз. Заказ

Рязанский государственный радиотехнический университет.

Источник

№ наблюдения	ti, с	ti— , с	(ti— ) 2 ,с 2
1	0,549	-0,008	0,000064
2	0,565	0,008	0,000064
3	0,548	-0,009	0,000081
4	0,554	-0,003	0,000009
5	0,571	0,014	0,000196
Суммы	ti=2,787