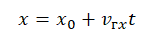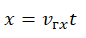Движение автомобилей задается уравнением x1 2t

Движение двух автомобилей по шоссе задано уравнениями x1=2t+0,2t^2 и x2=80-4t

Условие задачи:

Движение двух автомобилей по шоссе задано уравнениями \(x_1=2t+0,2t^2\) и \(x_2=80-4t\). Найти время и место встречи автомобилей.

Задача №1.7.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

Когда эти два автомобиля встретятся, их координаты будут равны. Поэтому, чтобы найти время встречи \(t\) приравняем уравнения.

Решим получившееся квадратное уравнение, для чего найдем дискриминант.

\[D = 900 + 4 \cdot 400 = 2500\]

\[\left[ \begin
t = 10 \; с \hfill \\
t = – 40 \; с \hfill \\
\end \right.\]

Получили два корня, один из которых не может являться ответом, поскольку он отрицательный. Теперь, чтобы найти место встречи автомобилей, нужно подставить полученное время в любое из уравнений. Будет легче всего, если подставить во второе.

\[x = 80 – 4 \cdot 10 = 40\; м\]

Ответ: 10 с, 40 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

Уточнение. Водитель x1 опомнился и повернул назад при времени t= – 5 c.
И через 5 с “начался” отсчет времени по задаче…
Очевидно водитель x1 хотел предупредить водителя x2 о том, что того ждет впереди…

Почему не учтен второй ответ?
Автомобили (до “начала решения задачи”) встречались 40 с назад…

40 c назад они ехали в одну сторону. Потом (через некоторое время) водитель x1 “опомнился” (это как раз время t=0) и поехал назад. Вот тут-то через 10 с они и встретились…

Давайте не будем наводить смуту в умах людей и условимся, что в подобных задачах имеет смысл только положительное время (т.е. после начала отсчета).
Просто отрицательное время может появляться в различных задачах, например, на движение тела, брошенного под углом к горизонту, где оно точно не будет иметь смысла, а Вы можете их натолкнуть на поиск объяснения отрицательного корня.
Соглашусь, что некоторый анализ корней уравнения всё же нужен, но переусердствовать тоже не стоит.

Источник

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Отсюда t₁ = 0 с, а t₂ = 6 с. Первый корень нам не подходит — из условия задачи уже было понятно, что тела начали движение одновременно. Снова они встрется, когда пройдет 6 секунд.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает вид:

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два корня: t₁ = 0,6 с, а t₂ = 3,4 с. Первый корень не подходит, так как в это время Саша еще не начал движение. Второй корень подходит, так как он меньше 4 с. Значит, Саша догонит Мишу через 3,4 с после того, как Миша начнет движение.

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет вид:

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Самостоятельная работа по физике в 10 классе на тему «Равномерное движение»

С.Р. 1 Путь, перемещение, прямолинейное равномерное движение. 10 класс. Вариант 1.

Движение двух велосипедистов заданы уравнениями:

На рисунке представлены графики зависимости координаты от времени.

Какова скорость 1 тела, в какой момент времени второе тело начало двигаться?

Две машины движутся по дороге с постоянными скоростями 10 м/с и 15м/с. Начальное расстояние между телами 1 км. Через сколько времени второе тело догонит первое.

С.Р. 1 Путь, перемещение, прямолинейное равномерное движение. 10 класс. Вариант 2.

Определите по графику какова была скорость тела на различных участках цепи, опишите характер движения.

3. Автомобиль и велосипедист движутся навстречу друг другу со скоростями 20 м/с и 5 м/с. Расстояние между ними в начальный момент времени 250 м. В какой момент времени и где они встретятся. Напишите уравнение движения каждого тела относительно точки, в которой находился велосипедист в начальный момент времени.

С.Р. 1 Путь, перемещение, прямолинейное равномерное движение. 10 класс. Вариант 3.

Опишите характер движения каждого тела. Найдите: начальную координату, величину и направление скорости каждого тела. Постройте графики зависимости х( t ). Найдите место и время встречи графически и аналитически.

На рисунке 1 представлены графики зависимости координаты от времени. Какова скорость 2 тела, какое расстояние было между телами в тот момент, когда 2 тело пришло в движение?

Колонна машин движется по шоссе со скоростью 10 м/с, растянувшись на 2 км. Из хвоста колонны выезжает мотоциклист со скоростью 20 м/с и движется к голове колонны. За какое время он достигнет головы.

С.Р. 1 Путь, перемещение, прямолинейное равномерное движение. 10 класс. Вариант 4.

Опишите характер движения каждого тела. Найдите: начальную координату, величину и направление скорости каждого тела. Постройте графики зависимости х( t ). Найдите место и время встречи графически и аналитически.

2. Со станции вышел товарный поезд со скоростью 36 км/ч. Через 30 минут в том же направлении вышел скорый поезд со скоростью 72 км/ч. Через сколько секунд после выхода товарного поезда его нагонит скорый?

4. По графику определите проекции скорости каждого тела, начальные координаты. Напишите уравнения х( t ).

Источник