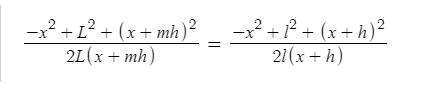Два автомобиля одновременно выехали навстречу друг другу
Два автомобиля одновременно выехали навстречу друг другу. Первый ехал со скоростью 75 км/ч, второй со скоростью 65 км/ч. Какое расстояние было между ними, если они встретились через 3 часа?
75 + 65 = 140 км/ч — скорость сближения
140 х 3 = 420 км — расстояние между ними.
Задача 2. Два автомобиля одновременно выезжают навстречу друг другу из двух городов, расстояние между которыми 456 км. Скорость первого автомобиля 68 км/ч а скорость второго на 16 км/ч больше. Через сколько часов они встретятся?
Скорость второго: 68 + 16 = 84 км/ч
68 + 84 = 152 км/ч — общая скорость
456 : 152 = 3 часа — через это время автомобили встретятся.
Задача 3. Два автомобиля выехали одновременно навстречу друг другу и через три часа встретились. Один автомобиль ехал со скоростью 80 километров час другой 90 километров час. Какое расстояние было между ними в начале пути Решите задачу двумя способами
80 + 90 = 170 км/ч — скорость сближения
170 х 3 = 510 км — первоначальное расстояние между автомобилями.
80 х 3 = 240 км — проехал первый автомобиль.
90 х 3 = 270 — проехал второй автомобиль
240 + 270 = 510 км — между пунктами отправления
Как решить задачу: два автомобиля едут навстречу друг другу. Скорость (см)?
Второй вариант или способ решения можно назвать «физическим». Находим относительную скорость одного автомобиля относительно другого, например первого относительно второго. vотн = v1 + v2 = 60+70 = 130 км/час (если тела движутся навстречу друг другу, то скорости складываются). Значит, первый автомобиль пройдет относительно второго путь равный 325 км (130*2,5=325). Ответ: 325 км.
Скорость сближения автомобилей равна 60 +70 =130 км/ч. Расстояние между автомобилями в начале движения было 130*2,5=325 км.
Автомобили едут навстречу друг другу,поэтому складываем их скорости и получаем: 60+70=130км/ч. Едут они 2,5часа (2часа и 30минут),тогда 130 * 2,5 = 130+130+65=325 км.
Другим способом: сколько проедет каждый — 60*2,5=150км.проедет первый, а второй 70 * 2,5 =175км.Теперь сложим — 150 +175 = 325км.
Ответ:325км. Расстояние между ними.
Минимизация по всем законам геометрической оптики должна сводиться к том, что отрезки от пунктов до реки параллельны
имеем два прямоугольных треугольника с общим катетом длиной а и
Из второго вычитаем первое
Точку А, спроецированную на берег реки назовём A’
Точку B, спроецированную на берег реки назовём В’
Если я правильно понял третью фразу задачи
x=0,16841, с точностью до округления 0,168
Может, чего в вычислениях я и соврал, но на глазок так вроде катит
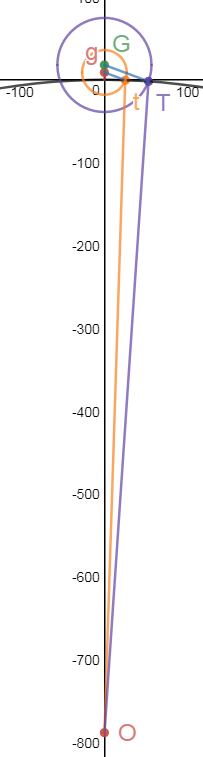
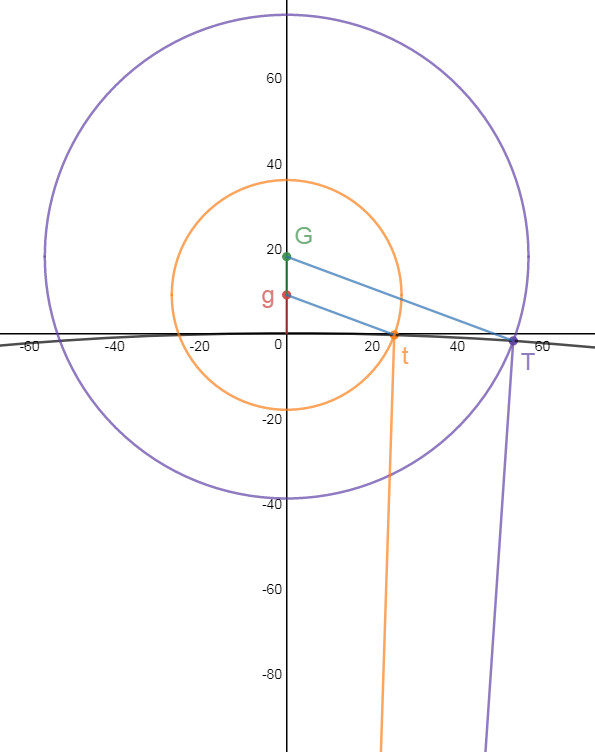
Лучи света, прошедшие через две точки, на высоте 9 и 18 километров, оставят след на поверхности спутника. Это дает нам возможность рассмотреть два треугольника с вершинами в центре спутника (точка О). Треугольники OTG и Otg
Все стороны треугольников нам известны. Более того, лучи света, пришедшие со столь далекого расстояния, будут параллельны между собой. Значит отрезки GT и gt параллельны между собой и составят с вертикалью одинаковый угол. Выразим этот угол из теоремы косинусов для двух треугольников и приравняем выражения.
«Х» заменяет R, а «m» коэффициент увеличения высоты горы. В данном случае он равен двум.
В результате преобразования, уравнение примет вид:
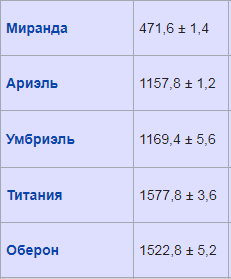
Ближайший по размеру спутник Урана это Титания.
Несмотря на простое решение, задача очень интересна и своеобразна. В этом можно убедиться при изменении исходных параметров задания. Математическая модель ведет себя несколько неожиданно и даже выдает «пятое измерение».
Решений предоставлено достаточно, но ответы не совпадают. Попробую решить эту задачу, так как это я понимаю. Все разговоры о плагиате, желающие высказаться, оставляють при себе.
Картинка к задаче не соответствует действительности. Дело в том, что если изображать шары в виде окружностей, то на виде с любой стороны параллелепипеда, они будут выглядеть, как две пересекающиеся окружности. Для того, чтобы увидеть касание окружностей их нужно рассматривать в плоскости перпендикулярной основанию и проходящей через центры шаров. В моем случае, это плоскость G-G.
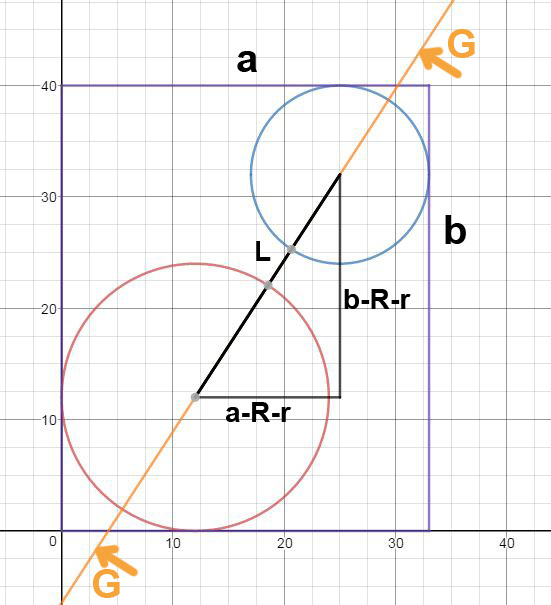
Возьмем коробку и шары произвольного размера. Разместим их в диагонально противоположных углах параллелепипеда. На виде сверху это будет выглядеть следующим образом. Где a и b ширина и длина коробки, соответственно.
По теореме Пифагора несложно посчитать размер между осями шаров, перпендикулярных основанию коробки (L).
Подставив в формулу значения из условия задачи, получим L=4sqrt(13)=14.422
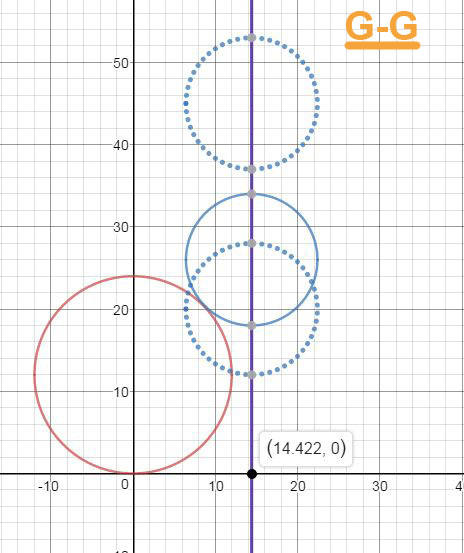
Далее рассмотрим картинку в плоскости G-G
Расстояния между осями определено. Большой шар условно неподвижен, а маленький может перемещаться по вертикали. Естественно, нас интересует только вариант, когда окружности соприкасаются в одной точке.
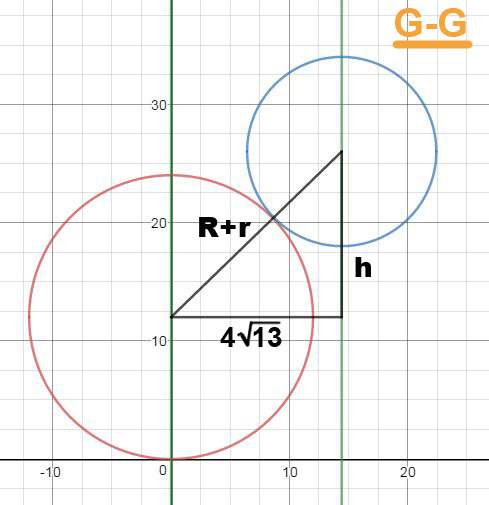
Рассмотрим эту схему подробнее.
Опять же, несложно по Пифагору определить расстояние между центрами шаров, по вертикали.
При подстановке значений получим h=6.928
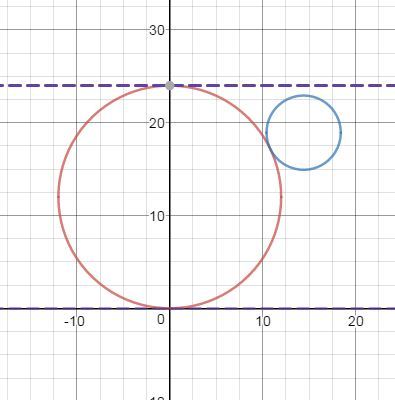
Очевидно, что маленький шар спокойно поместится в свободный угол коробки и не будет принимать участие в формировании высоты коробки. А это значит, что высота коробки будет принята по размеру большого шара, то есть:
Высота коробки будет равна 24.